今回は中2で学習する
確率の単元の中から
硬貨を同時になげるときの問題を徹底解説していくよ!

硬貨の確率は、とっても単純だから
この記事を通してマスターしていきましょう!
今回の内容をサクッと理解したい方はこちらの動画がおススメです^^

硬貨を投げる問題では樹形図を書く!
硬貨を投げる確率問題では
樹形図を書いて考えていくと、とってもラクになります。
樹形図といってもすごくシンプルなモノです。
表を〇、裏を×と考えて
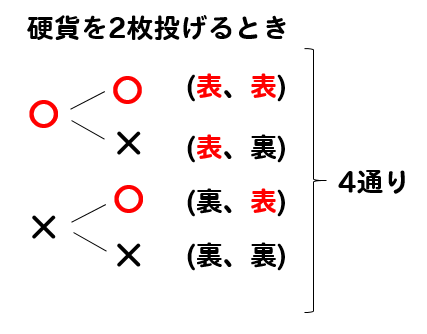
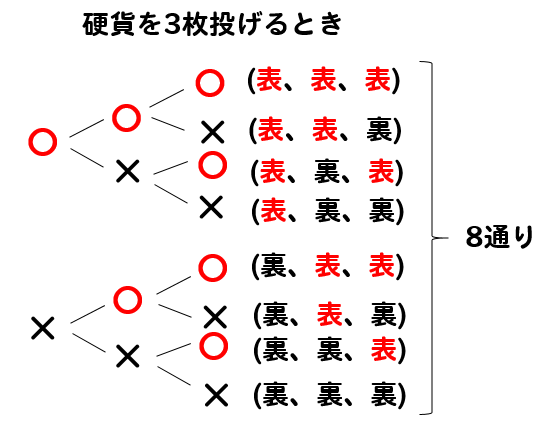
このように樹形図を書いて
問題を考えていきます。
それでは、この樹形図を使って
パターンごとに問題を解説していきます。
硬貨の基本問題の解説!
まずは、硬貨の基本問題について見ていきましょう。
硬貨を2枚投げるときの確率
2枚の硬貨を同時に投げるとき、1枚が表で1枚が裏になる確率を求めなさい。
それでは、この問題を先ほどの樹形図を使って考えてみましょう。
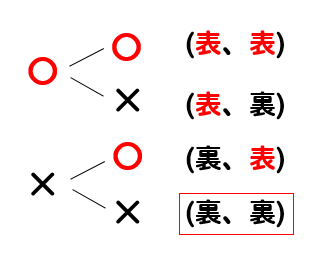
2枚の硬貨を投げるときの樹形図を見て
1枚が表、1枚が裏になっているところを見つけると
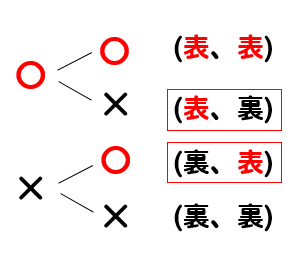
このように2つ見つかります。
よって、確率は
$$\frac{2}{4}=\frac{1}{2}$$
となります。
樹形図を書くことができれば
あとは問題の条件に合うところを見つけていくだけです。
とーーーっても簡単ですね(^^)
それでは、硬貨を3枚投げるときの問題も考えてみましょう。
硬貨を3枚投げるときの確率
3枚の硬貨を同時に投げるとき、1枚が表で2枚が裏になる確率を求めなさい。
今度は、3枚の硬貨を投げる問題なので
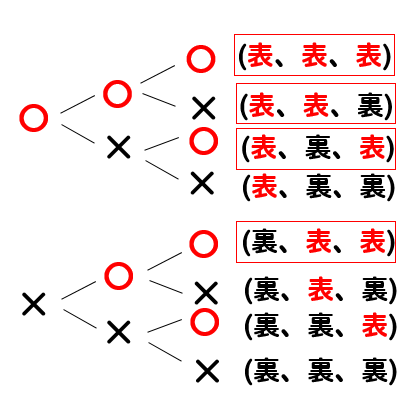
3枚硬貨の樹形図を見ながら、〇が1つで×が2つになっているところを見つけます。
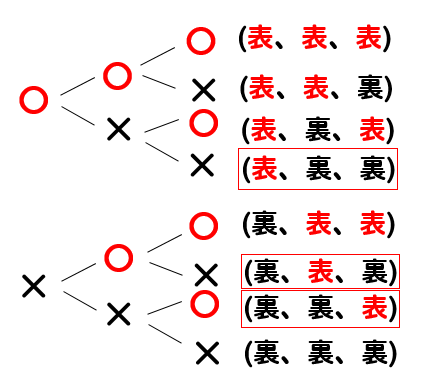
すると、3つ見つかるので確率は
$$\frac{3}{8}$$
となります。
こちらも樹形図を書くことができれば
楽勝な問題ですね!
だから、硬貨の確率をマスターしようと思ったら
まずは樹形図を書く練習をすることが大切です。
練習問題を用意しておいたので
樹形図を書く練習も含めて挑戦してみてください!
演習問題で理解を深める!
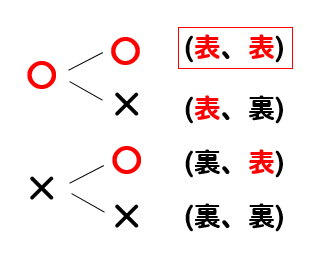
2枚の硬貨を同時に投げるとき、2枚とも表になる確率を求めなさい。
1枚の硬貨を3回投げるとき、硬貨の表が2回以上出る確率を求めなさい。
硬貨の発展問題の解説!
それでは基本問題をマスターしてもらったところで
少しだけ発展させた問題を考えていきましょう。
金額を考える確率
10円硬貨、50円硬貨、100円硬貨を同時に3枚投げるとき、表が出た硬貨の合計が100円以上となる確率を求めなさい。
問題を読んだだけでは
なんか複雑そう…

と、なってしまいますが
これも非常に簡単な問題です。
3枚硬貨の樹形図を使って
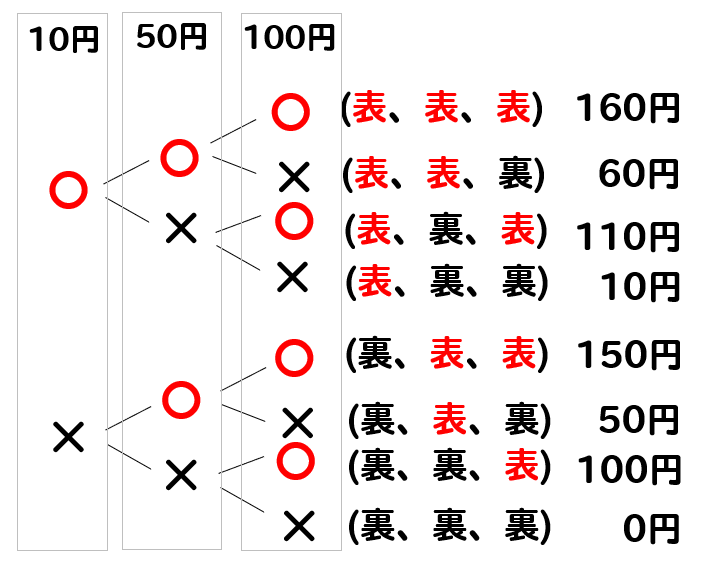
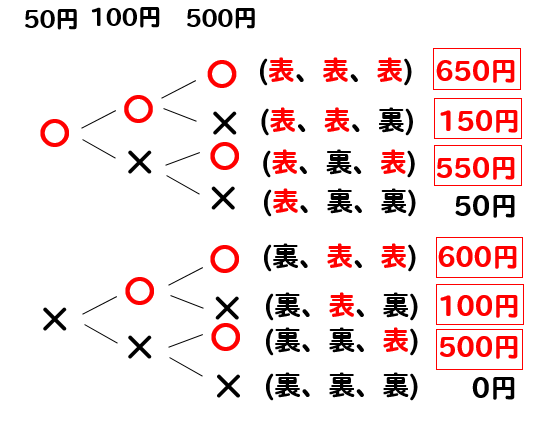
このように考えていきます。
1つ目の〇×を10円硬貨
2つ目の〇×を50円硬貨
3つ目の〇×を100円硬貨と考えて
それぞれの合計金額を出してやります。
すると、この中から合計金額が100円以上となっているのは
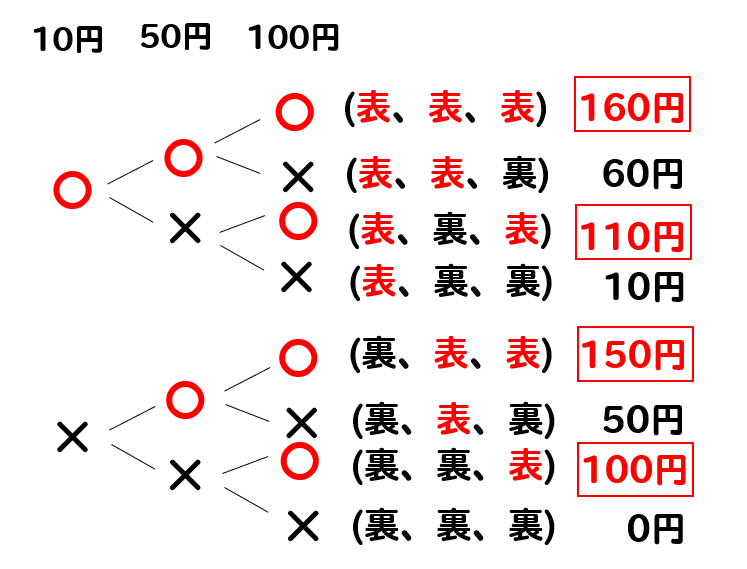
4つ見つかるので、確率は
$$\frac{4}{8}=\frac{1}{2}$$
となります。
金額を考える確率でも
基本問題と同様、樹形図がしっかりと書ければ楽勝です!
それでは、演習問題にも挑戦してみましょう。

演習問題で理解を深める!
50円硬貨、100円硬貨、500円硬貨を同時に3枚投げるとき、表が出た硬貨の合計が100円以上となる確率を求めなさい。
少なくとも~を考える確率
3枚の硬貨を同時に投げるとき、少なくとも1枚は表が出る確率を求めなさい。
『少なくとも1枚は表が出る』
というのは
『表が1枚、2枚、3枚のどれかが出る』
ということを表しています。
んーややこしいですね。

なので、『少なくとも』というワードが出てきたら
それ以外のことを考える。
というのが確率の鉄則です。
つまり

すべて裏になる確率を考えます。
すべて裏になる確率は
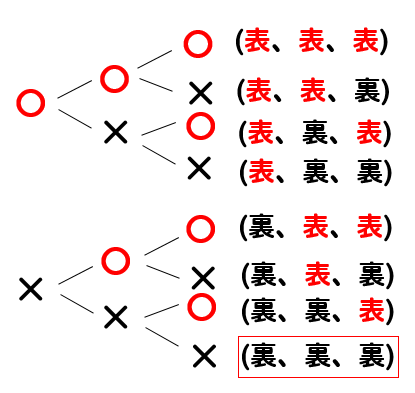
樹形図から\(\frac{1}{8}\)となります。
このように
求めたいモノ以外の確率が出せたら
1(全体)から引いてやります。
$$1-\frac{1}{8}=\frac{7}{8}$$
そうすることで、少なくとも1枚は表になる確率は\(\frac{7}{8}\)ということが求められました。
全体から、それ以外のモノを引いてやれば
求めたいものだけが残りますよね。
少なくとも~を正面から考えていくと、ちょっと複雑なので
一旦はそれ以外の確率を求める。
そして、それを全体から引いてやると求めたいものが出てくる。
こういう考え方で解いていくと、楽に求めることができます。
中学数学では、そこまで複雑なモノは出てこないので
この考え方はそんなに出番がないかもしれませんが
高校数学では、めちゃめちゃ使う大切な考え方だから
頭の片隅にでも置いといてもらえると、今後の役に立つかな~って思います(^^)
よければ演習問題も挑戦してみてください。
演習問題で理解を深める!
2枚の硬貨を同時に投げるとき、少なくとも1枚は表が出る確率を求めなさい。
テストに強くなる!確率の点を伸ばす定期対策ドリルをプレゼント!
お疲れ様でした^^
これで硬貨の確率のやり方は理解してもらえたと思います!
ただ、今回のようにさいころだけ、硬貨だけ、玉を取り出すだけ…のようにパターン別に演習をやっていると、頭を使うことなく流れで解けてしまうことが多いです。
実際のテストではどのパターンが出題されるかはランダムであり「表を使って考える?」「樹形図を使って考える?」といったことを問題文から解法を瞬時に判断していかないといけません。
というわけで!
今回は確率のテスト対策として、「問題⇒パッと解き方を判断」という特訓ができるような実戦演習を用意しました。

動画解説もつけているので苦手なお子さんでも1人で取り組めますよ^^
確率は他の単元に比べて、難しい公式、計算が出てこないので、数学をニガテにしている方でも点が伸ばしやすいです!なので、今回の課題も活用しながら、早めのテスト対策をしていきましょう(‘ω’)ノ
【定期対策ドリル】確率基礎を無料で受け取る!
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
硬貨を投げるときの確率 まとめ
お疲れ様でした!
硬貨を投げるときの確率は
樹形図を書くこと
これがポイントです。
というか、コレしかありません。
樹形図を書くことができれば楽勝な問題です。
硬貨の問題、苦手だな…という人は
まず、樹形図を書く練習をする。
そして、いろんな問題を解いて樹形図を見ることに慣れる。
これに尽きます。
硬貨の確率問題は今日でマスターしちゃいましょう!
ファイトだー(/・ω・)/














質問です。
上記金額考える問題中で10円、50円、100円の3種類の効果を使い、表の合計金額が100円を超える確率の回答が3/8と解説がありますが、樹形図7段目の硬貨の表が100円一枚だった時の金額が10円となっている理由が判りません。
ご教授いただければ幸いです。
申し訳ありません。
こちらの記述ミスでした…正しくは100円となります。
訂正しておりますので、ご確認いただければと思いますm(__)m
ご指摘ありがとうございました!