今回は中3で学習する「因数分解」の単元から、置き換えを利用した解き方について解説していきます。
取り上げるのはこちらの3題！
次の式を因数分解しなさい。
(1) \((x-2)^2-2(x-2)-35\)
(2) \((a+b)^2-16\)
(3)\(ab-4a-b+4\)
うげぇ…めっちゃ複雑そうなんだけど…
たしかに！
発展的な問題になるんだけど、これが解けるようになれば定期テストでも高得点まちがいなしだ！
だから、がんばって理解していこう(^^)
（1）同じ部分は置き換えろ！
次の式を因数分解しなさい。
(1) \((x-2)^2-2(x-2)-35\)
それでは、最初の問題の解き方を解説していきます。
解き方のポイントは
同じ部分は置き換えろ！
です。
どういうことかと言うと
因数分解したい式に、このような同じ部分が含まれている場合
置き換えという考え方を利用してやります。
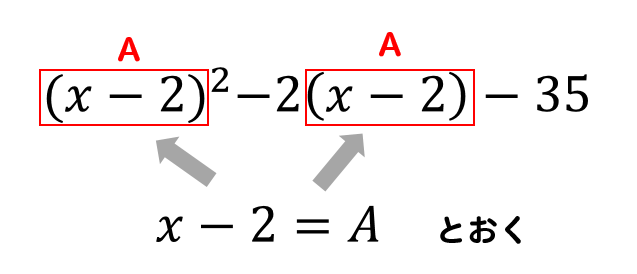
そうすることによって、複雑だった式がシンプルになりますね！
$$\large{A^2-2A-35}$$
あとは、この式を因数分解していけば良いです。
$$\large{A^2-2A-35}$$
$$\large{=(A-7)(A+5)}$$
因数分解が完成したら
置き換えていたAを元に戻してやります。
$$\large{=\{ (x-2)-7\}\{(x-2)+5\}}$$
$$\large{=(x-9)(x+3)}$$
これで完成となります！
初めは複雑な式で、どのように因数分解していけばいいのか分かりにくかったですが、同じ部分を置きかえしてあげることでシンプルな方法で解くことができましたね(^^)
では、解法をまとめておきます。
$$\large{(x-2)^2-2(x-2)-35}$$
$$\large{=A^2-2A-35}$$
$$\large{=(A-7)(A+5)}$$
$$\large{=\{ (x-2)-7\}\{(x-2)+5\}}$$
$$\large{=(x-9)(x+3)}$$
答え
$$（1）(x-9)(x+3)$$
（2）かたまりを文字で置いてみると…？
次の式を因数分解しなさい。
(2) \((a+b)^2-16\)
（1）のように同じ部分があるわけではないんですが、\((a+b)\)のかたまりを文字で置いてあげると…
このように『2乗－2乗』の形がつくれるので、上手いこと因数分解をしていくことができますね！
最初に2乗を展開してしまうと、困ったことになってしまうので注意です…(^^;)
答え
$$（2）(a+b+4)(a+b-4)$$
（3）同じ部分が無い場合には！？
次の式を因数分解しなさい。
(3)\(ab-4a-b+4\)
それでは、次にこちらの問題を考えてみましょう。
よっしゃ！置き換えを利用すればええんじゃろ？
余裕だぜっ！！
って、あれぇぇぇ
同じ部分がないやんけっ！
同じように置き換えを利用して解きたかったのですが、同じ部分が見つからず困ってしまいます…
そんなときには
同じ部分を発掘するのだ！
因数分解したい式を前半と後半部分に分けてしまいます。
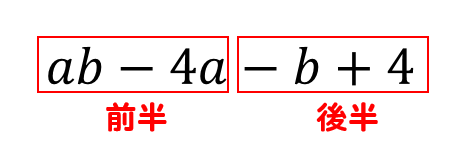
そして、それぞれの部分を因数分解してやります。
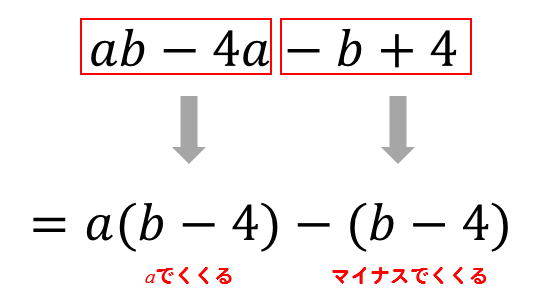
そうすることによって、同じ部分\((b-4)\)を発掘することができました！
同じ部分が発掘できたら、あとは置き換えを利用していけば良いですね。
$$\large{ab-4a-b+4}$$
$$\large{=a(b-4)-(b-4)}$$
\(b-4=A\)とおくと
$$\large{=aA-A}$$
$$\large{=A(a-1)}$$
$$\large{=(b-4)(a-1)}$$
これで因数分解が完成しました！
今回の式のように同じ部分が見つからない…という場合
前半、後半に分けて因数分解をしてあげることで、同じ部分を発掘することができることがあります。
答え
$$（3）(b-4)(a-1)$$
練習問題で理解を深める！
それでは、置き換えを利用した因数分解の理解を深めるために練習問題を解いてみましょう！
次の式を因数分解しなさい。
$$\large{(x-3)^2+5(x-3)-6}$$
次の式を因数分解しなさい。
$$\large{ab+ac-3b-3c}$$
まとめ
お疲れ様でした！
複雑な式の因数分解では、同じ部分が見つかれば置き換えを利用することで簡単に解くことができます。
もっと難しい因数分解に挑戦したい方は
こちらの問題をやってみましょう！
これが解けるようになれば
中学レベル卒業だ！！
コメントを残す