【一次関数】座標の求め方は？いろんな座標を求める問題について解説！

こんにちは！数スタの小田です。

今回は一次関数の単元から

座標の求め方は？

という点において解説をしていきます。

 

一次関数…グラフは苦手だ…と感じている方も多いと思います。

だけど、やっていくことはただの計算問題！

別に難しいことではないんだよ(^^)

 

ということで、この記事を通して一次関数の座標を求める問題はマスターしちゃおう！

 

今回の記事はこちらの動画でも解説しています(/・ω・)/

 

【一次関数】座標の求め方は？いろんな座標を求める問題について解説！

一次関数の座標を求める問題では、大きく分けて４つのパターンがあります。

それでは、それぞれのパターンについて座標の求め方について解説していきます。

ポイントは…

式に代入だ！！

\(y\)軸との交点の座標の求め方

 

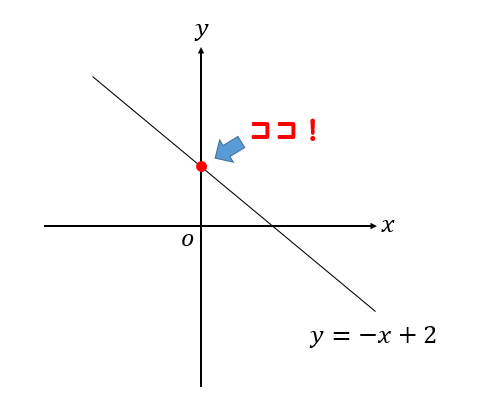
\(y\)軸との交点、それは言い換えると…

\(x\)座標が０の場所だ！

ということなので、一次関数の式 \(y=-x+2\) に \(x=0\) を代入しましょう。

すると

$$y=0+2=2$$

よって、\(y\)軸との交点は \((0.2)\) ということが分かります。

また、\(y\)軸との交点は切片とも呼ばれ

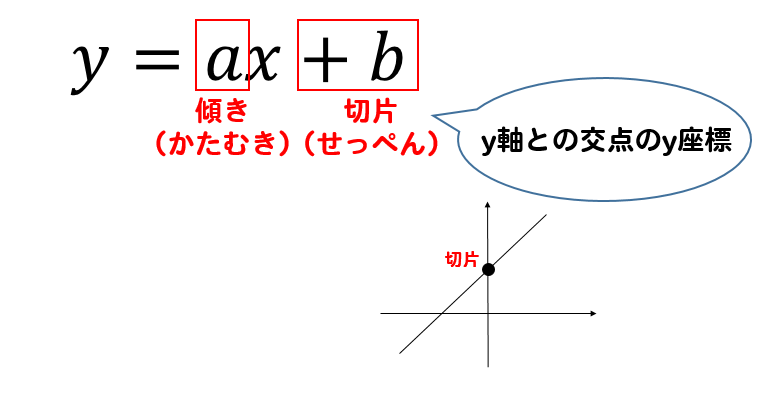
一次関数の\(b\)部分を見ることですぐに求めることもできます。

 

 

\(x\)軸との交点の座標の求め方

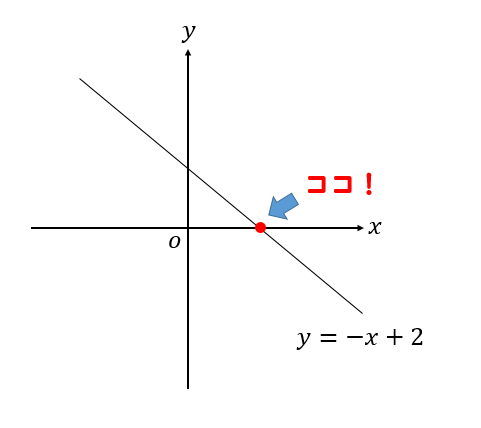
\(x\)軸との交点、それは言い換えると…

\(y\)座標が０の場所だ！

ということなので、一次関数の式 \(y=-x+2\) に \(y=0\) を代入しましょう。

すると

$$0=-x+2$$

$$x=2$$

よって、\(x\)軸との交点は \((2.0)\) ということが分かります。

 

\(y=0\) を代入する！たったこれだけのことですね(^^)

 

直線上のどこかの座標の求め方

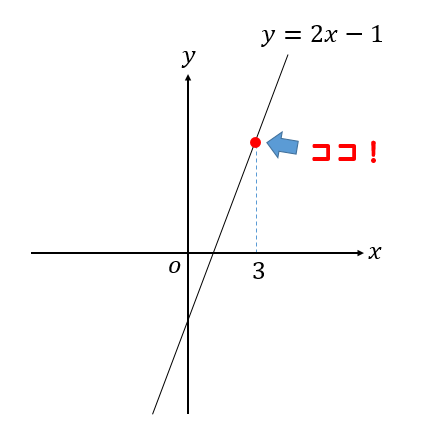
\(x\)軸や\(y\)軸の座標ではない場合、今回の問題のように\(x,  y\)どちらかの座標が分かれば求めることができます。

今回の問題では、\(x=3\) であることが分かってるので、これを一次関数の式 \(y=2x-1\)に代入します。

すると

$$y=2\times 3-1=6-1=5$$

このように点Aの \(y\) 座標を求めることができます。

よって、点Aの座標は\((3,  5)\) ということが求まりました。

 

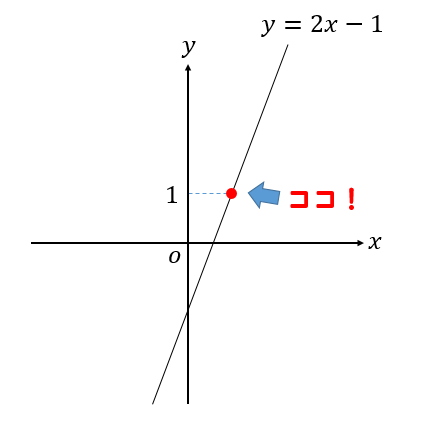
\(y\)座標が与えられているのであれば、それを一次関数の式に代入すればOK！

$$1=2x-1$$

$$-2x=-1-1$$

$$-2x=-2$$

$$x=1$$

よって、点Aの座標は\((1,  1)\)ということが求まりました。

このように、求めたい点の\(x,  y\)どちらかの座標が分かれば、それを一次関数の式に代入することで簡単に座標を求めることができます。

２直線の交点の座標の求め方

 

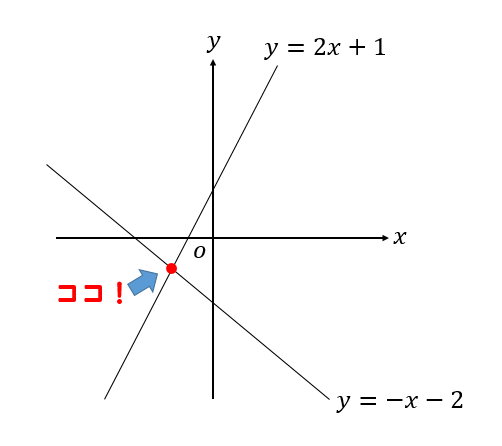
２直線の交点の座標は…

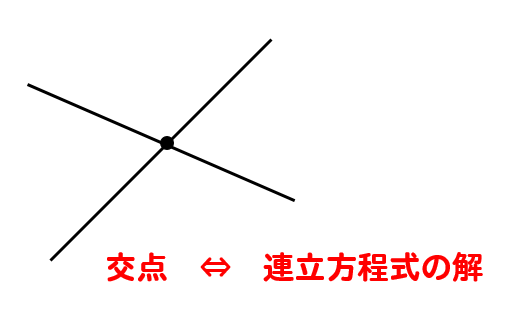
それぞれの式を連立方程式で解いたときに出てくる解と等しくなります。

 

なので、2直線の交点を問われば

連立方程式を解くべし！

 

ということで

$$\begin{eqnarray} \left\{ \begin{array}{l}y=2x+1 \\y=-x-2 \end{array} \right. \end{eqnarray}$$

この連立方程式を解いていきましょう。

一次関数の交点を求める場合の連立方程式は、ともに\(y=…\)の形になっていることが多いので代入法で解くとラクですね。

 

\(y=2x+1\) に\(y=-x-2\) を代入すると

$$-x-2=2x+1$$

$$-x-2x=1+2$$

$$-3x=3$$

$$x=-1$$

\(x=-1\) を\(y=2x+1\) に代入すると

$$y=-2+1=-1$$

よって、2直線の交点は\((-1,  -1)\) ということが求まりました。

 

ちょっと応用！追加演習を用意しました！

さて、ここまでのところで座標の求め方はバッチリですね！

あとは何も見ないで自力で解けるかどうかをチェックしていきましょう(‘ω’)ノ

というわけで、追加演習を用意しました！

 

• 問題のプリントはこちら！

 

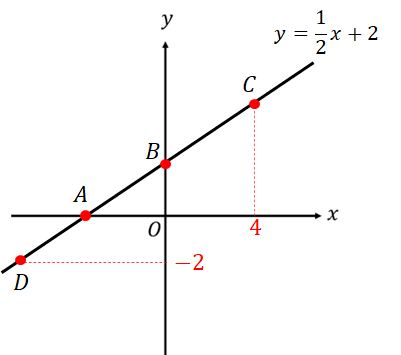
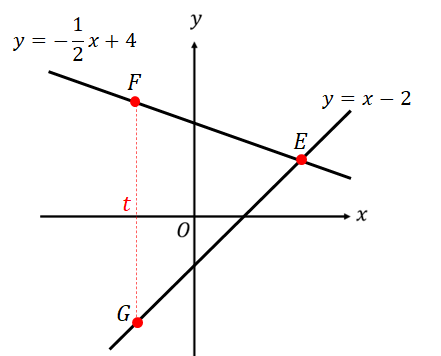
Ｆ、Ｇの2点については\(x\)座標が文字になっています！

これをどうやって対処すればいいか分かりますか？？

こういった問題が解けるようになると、一気に応用力が高まってきますよ＾＾

 

「追加演習やったよ～！」

「解けなかったので解説して欲しいです…！」

という方には、こちらから解答＆動画解説を送らせてもらっています(‘ω’)ノ

しっかりと最後までやりきってレベルアップしていきましょうね＾＾

 

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れます＾＾

（ご登録いただいたメールアドレスに解説を送らせていただきます）

 

答えが合っているかどうかだけでなく、動画解説を活用して『立式のポイント』『情報の読み取り方』といったところもチェックしておいてくださいね＾＾

解答を受け取ってくれた方には、引き続きいろんな問題をメールでお届けする予定なのでお楽しみに＾＾

【一次関数】座標の求め方まとめ！

お疲れ様でした！

座標の求め方は、基本的に式に代入するだけ。

2直線の交点を求める場合だけ連立方程式を解く必要がありますが、それも難しいものではありませんね(^^)

 

こんなに簡単に求めることができるのに苦手に感じている人が多いのが残念…

しっかりと解き方を頭に入れておいて、テストや入試では得点しちゃいましょう★