今回は高校数学Aで学習する
「方べきの定理」
についてサクッと解説しておきます。
一応、高校数学で学習する内容ではあるんだけど
相似な図形が理解できていれば解ける!
ってことで、高校入試で出題されることも多いみたい。
といわけで、今回の記事では
中学生にも理解できるよう、
方べきの定理について、そして問題の解き方について解説します(/・ω・)/
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
方べきの定理とは
【方べきの定理】
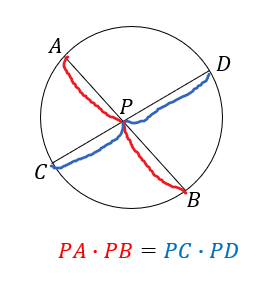
円の中で2直線が交わるとき、
それぞれの交点Pを基準として、一直線上にある辺の積が等しくなる。
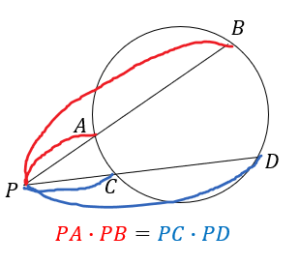
円を串刺しにするように2直線があるとき、
直線の交わる点Pを基準として、一直線上にある辺の積が等しくなる。
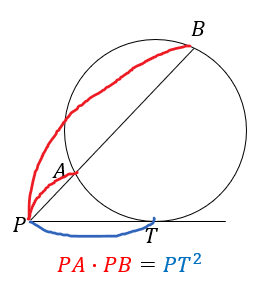
2直線のうち、1つの直線が円と接するとき、
接しているほうの辺は二乗となる。
なぜこのような定理が成り立つのかというと
それは相似な図形を考えると簡単に理解できます(^^)
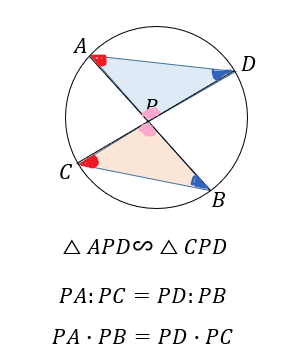
それぞれの円では、
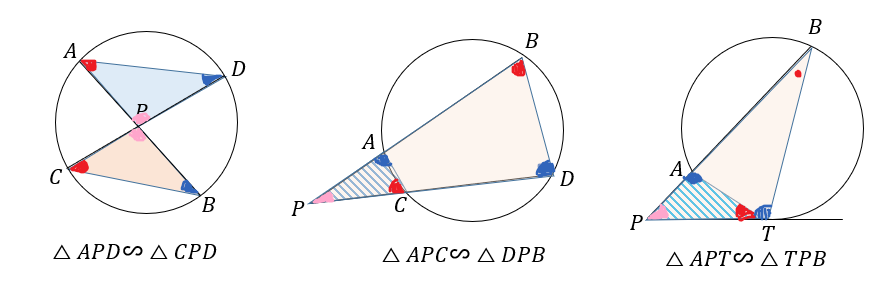
このように相似な三角形を見つけることが出来ます。
そして、それらの対応する辺に注目して
相似比を考えていくと、上で紹介したような
方べきの定理を導くことができます。
ただ、毎回相似な図形を見つけて、相似比を…
として問題を解いていくのはめんどうなので、
方べきの定理として、辺の関係を覚えておくといいでしょう。
方べきの定理を使って問題を解いてみよう!
それでは、方べきの定理を使った問題に挑戦してみましょう!
【問題】
次の図において、\(x\)の値を求めなさい。
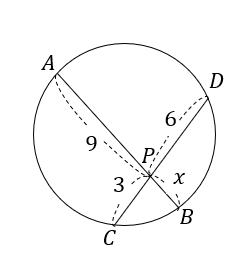
方てべきの定理に当てはめて考えてみると
$$\begin{eqnarray}PA\cdot PB&=&PC \cdot PD\\[5pt] 9\cdot x&=&3\cdot 6\\[5pt]9x&=&18\\[5pt]x&=&2\cdots(解)\end{eqnarray}$$
【問題】
次の図において、\(x\)の値を求めなさい。
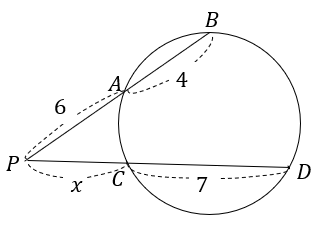
こちらも方べきの定理に当てはめて解いてみましょう。
気を付けるのは、PB、PDの長さを用いるという点です。
$$\begin{eqnarray}PA\cdot PB&=&PC \cdot PD\\[5pt] 6\cdot 10&=&x\cdot (x+7)\\[5pt]60&=&x^2+7x\\[5pt]x^2+7x-60&=&0\\[5pt](x+12)(x-5)&=&0\\[5pt]x>0より&&\\[5pt]x&=&5\cdots(解)\end{eqnarray}$$
【問題】
次の図において、\(x\)の値を求めなさい。

方べきの定理に当てはめてみると
$$\begin{eqnarray} PA\cdot PB&=&PT^2\\[5pt]4\cdot 9&=&x^2\\[5pt]36&=&x^2\\[5pt]x>0より&&\\[5pt]x&=&6\cdots(解)\end{eqnarray}$$
ちょい発展演習
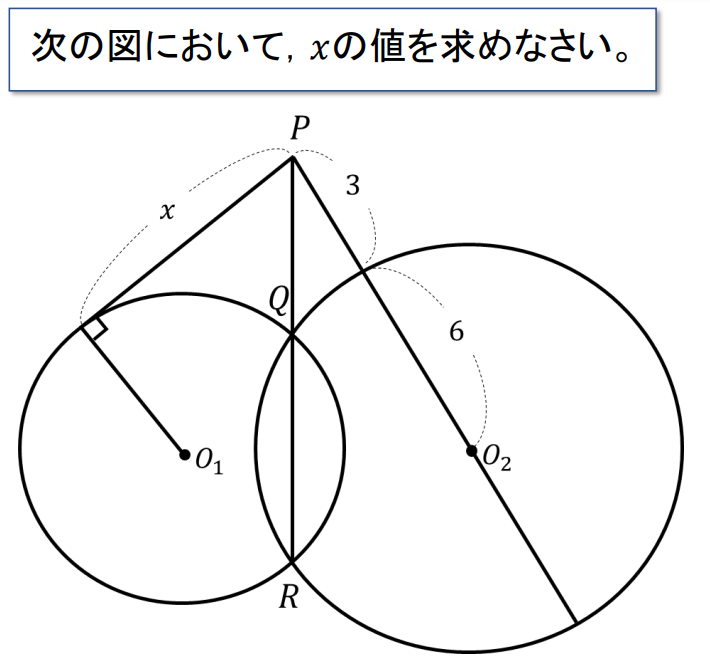
【解答】
2つの円において、それぞれ方べきの定理で式をつくる ⇒ それらを連立方程式(代入)で解いていけばOKです!
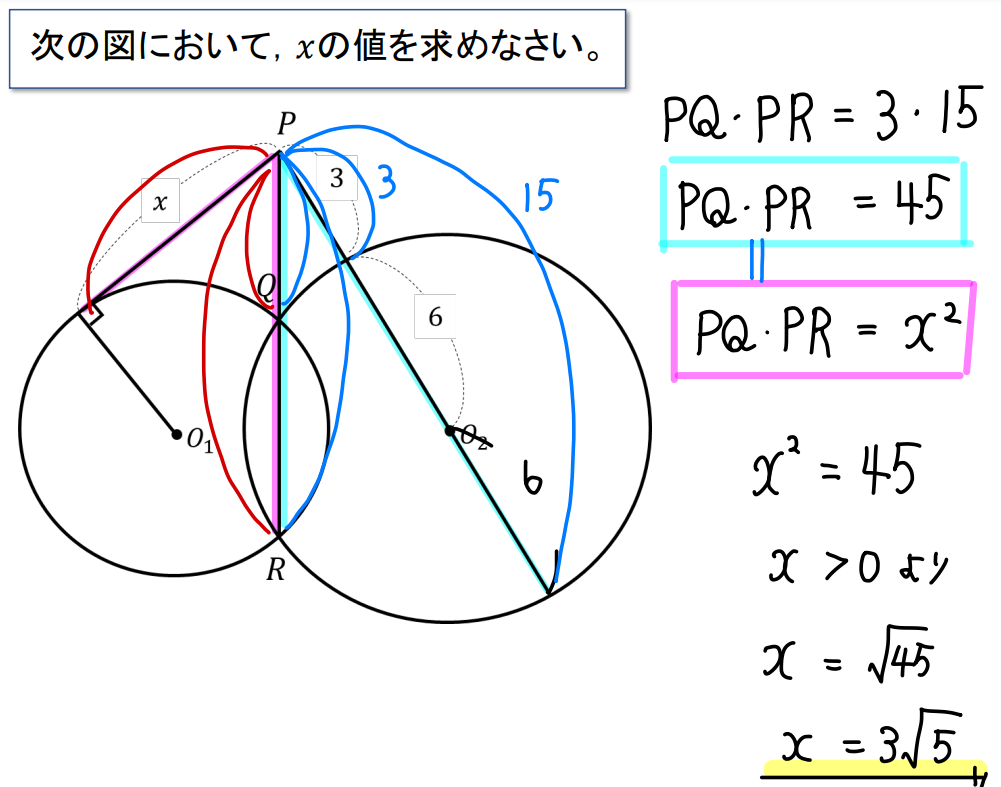

【解答】
図をイメージするところが難しいですが、1度理解しておけば次からは迷うことはありませんね^^

まとめ!
お疲れ様でした!
方べきの定理、簡単でしたね(^^)



このように、円に対して2直線が突き刺さっているような図が出てきたら方べきの定理の出番です。
しっかりと特徴を覚えておきましょう(/・ω・)/














中学三年生の受験生です。方べきの定理が理解できず、格闘していましたが、わかりやすく解説していただき、ありがとうございます。
お役に立てて良かったです!
受験勉強ファイトです(‘ω’)ノ
高校の先生が説明するより分かりやすかったです!!
テスト範囲でもあったので助かりました。
ありがとうございます!!!
テスト範囲だったので助かりました‼️
ありがとうございます