こんにちは!数スタの小田です。
今回は高校数学Aで学習する図形の単元から「円に内接する四角形はどれ?」について取り上げます。
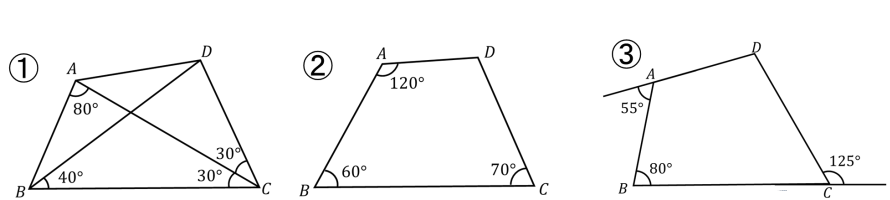
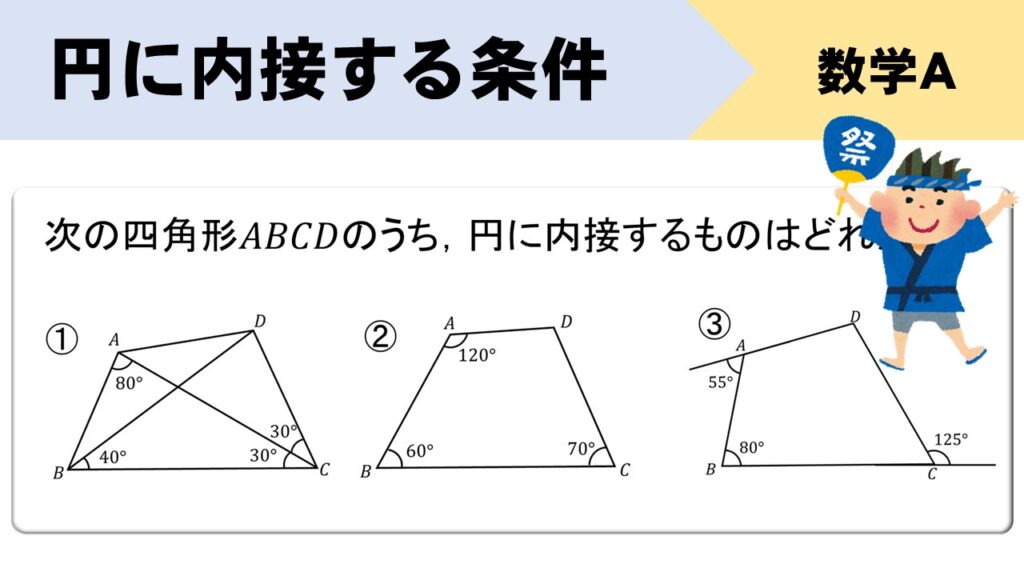
【問題】
次の四角形ABCDのうち、円に内接するものはどれか。
サクッと理解したい方は、こちらの動画も参考にしてください!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
円に内接する条件をおさえておこう!
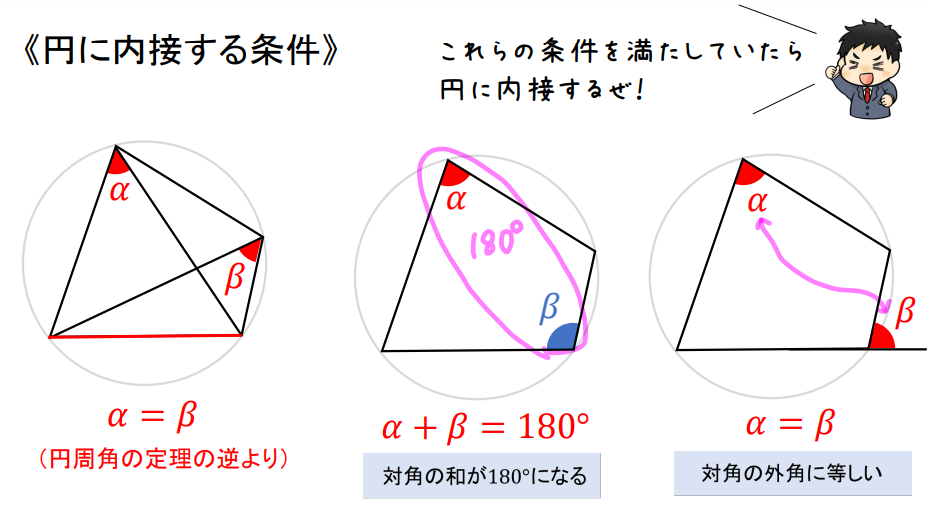
与えられた四角形がいずれかの条件を満たしていれば、円に内接します。
どの条件をチェックすればよいかは、与えられた図形の形を見ながら判断しましょう!
どれが内接する?問題の解説
では、①の図形から順にチェックしていきましょう。
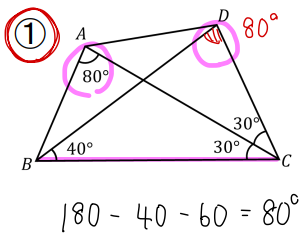
この四角形では対角線が引かれており、それに関する角の大きさがわかっているので【円周角の定理の逆】が成り立つかどうかをチェックしましょう。
すると、△DBCの内角に注目して、∠BDCの角の大きさを求めると80°となります。よって、∠BACと∠BDCが同じ大きさになっていることがわかりますので、条件クリア!
①の四角形は円に内接することがわかります。
【参考になる動画】
続いて②の図形を見てみましょう。
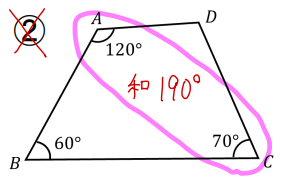
対角にある角の大きさが、70°、120°とわかっているので【対角の和が180°になる】かどうかをチェックしましょう。
70°と120°の和は190°となり、180°にはなりませんでした…条件クリアならず(._.)
ということで、②の四角形は円に内接しません。
最後に③の図形。
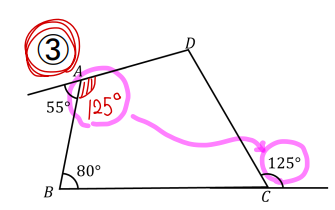
四角形の外角の大きさがわかっているので【対角の外角に等しい】かどうかをチェックしていきましょう。
55°のとなりにある内角は125°、その向かいにある外角もまた125°。
それぞれ同じ大きさになっているので、条件クリア!
ということで、③の四角形は円に内接します。
以上より、

円に内接する四角形は①③となります。
答え
①③
ちゃんと見るべきポイントがわかっていれば、簡単に判断することができますね^^
定期テストでは絶対に点を取りたい問題なので、しっかりと覚えておきましょう!
では、今回は以上。
円に内接する四角形と言えば、角度を求める問題もよく出題されます。
ここのところもしっかりとやっといてくださいね^^













コメントを残す