比例と反比例の違いは？見分け方はどうすれば良いか解説！

今回の記事では

比例と反比例の違いって何？

そもそも比例と反比例ってどういうものなの？

という、この単元における基礎の部分のお話をしていきます。

数学が得意っていう人でも

公式を丸暗記しているだけで

本質的な理解が出来ていない人も多いから

今回の記事で基礎の再確認をしてもらえたらと思います＾＾

比例・反比例の特徴

それでは、比例・反比例の特徴を確認しながら

それぞれの違いについて見ていきましょう。

比例の特徴とは

比例とは

のことを比例関係があると言います。

うーん…

これだけだと分かりにくいから具体例で見てみるね

1個100円のりんごを何個か買ったときの代金を考えてみる。

個数と代金の関係を表にしてみると

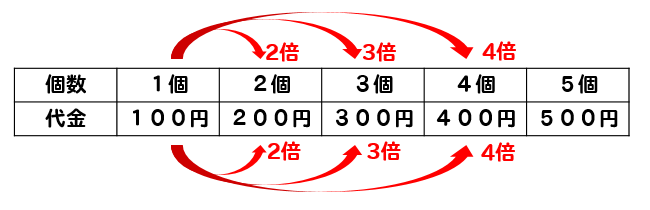
個数が2倍、3倍となれば代金も2倍、3倍となっていますよね

このような関係にあるとき『個数と代金は比例関係にある』といいます。

また『代金は個数に比例する』ともいいます。

ちなみに

表を使って横の変化について見てみると

一方が2倍、3倍ならもう一方も2倍、3倍という特徴が読み取れました。

では、表の縦の変化について見てみるとどんな特徴が読み取れますか？

そうですね

すべて100倍されているってことがわかります。

もちろん問題によって何倍されているかは変わるんだけど

比例の場合、常に一定の数が掛けられているという特徴があります。

このことを利用すると

(代金)＝100×(個数)

と表すことができます。

ちょっと数学っぽく

代金をy円

個数をx円としてやると

y＝100x

となります。

このことから比例の関係を式に表してやると

必ずy＝〇xとなることがわかります。

ちなみに、グラフで表すと

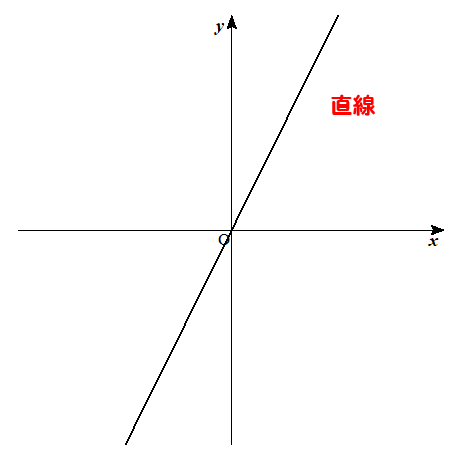
このように原点を通る直線になるという特徴もあります。

比例のグラフの書き方！分数が出てきても楽勝な方法とは？

以上のことをまとめておくと

反比例の特徴とは

反比例とは

のことを反比例の関係があると言います。

こちらも具体例で見てみましょう。

6mのリボンをx等分したときの1本分の長さをy mとすると

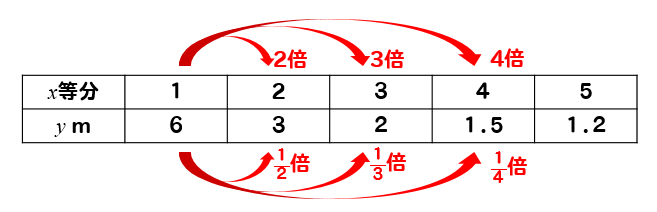
xの値を2倍、3倍すればyの値は1/2倍、1/3倍されていますね。

このような関係のとき『yはxに反比例する』といいます。

比例のときと同様に表の値を縦で見てみるとこのような特徴があります。

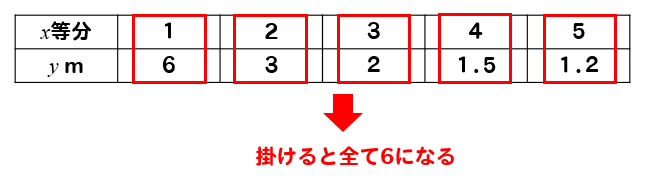
xの値とyの値を掛けると全て同じ値になっていますね。

反比例はxとyの値を掛けると常に一定の値になることから

式はこのように表せます。

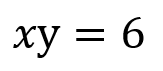
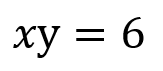
式は一般的にy＝の形で表すので、両辺をxで割って変形してやると

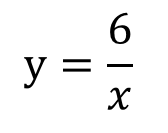
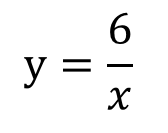
ちなみに、反比例をグラフで表すと

このように双曲線となります。

これらのことをまとめておくと

反比例とは

一方の値が2倍、3倍…となると、もう一方の値は1/2倍、1/3倍…となる関係

 

それぞれの関係を式に表すと

と表すことができます。

aは問題によっていろいろな数に変わりますが

このaのことを比例定数といいます。

※反比例だけど、比例定数ね！反比例定数とは言わないから注意！

 

グラフで表すと、双曲線になる。

比例と反比例の違いは

それでは、上の情報をまとめて

比例と反比例の違いについて確認しておきます。

比例の場合

一方が2倍、3倍…なら、もう一方も2倍、3倍…となっている。

それぞれの関係を式に表すと

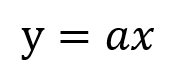
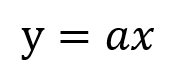
こういった式で表されます。

グラフは、直線になります。

反比例の場合

一方が2倍、3倍…なら、もう一方は1/2倍、1/3倍となっている。

それぞれの関係を式に表すと

こういった式で表されます。

グラフは双曲線になります。

比例・反比例の見分け方

このようにそれぞれの特徴を覚えておけば

比例と反比例の見分けもできるのではないでしょうか。

あれ？

これって比例？反比例？と困ったときには

表を書いて、それぞれの変化を見てみましょう。

同じように2倍、3倍されていくなら比例

2倍、3倍に対して1/2倍、1/3倍となっていくなら反比例ですね。

もしくはそれぞれの関係を式に表してみて確認しましょう。

y=ax の形になれば比例

y=a/x の形になれば反比例ということが分かります。

以上！

比例・反比例の違いについてでした。