今回は中1数学で学習する
「図形の対称移動」
についてまとめておきます。
対称移動ってどんな移動?
対称移動の作図ってどうやるの?
対称移動したときに重ねられる図形はどれ?
これらの疑問に対して、1つずつ答えていきますね(^^)
対称移動の特徴
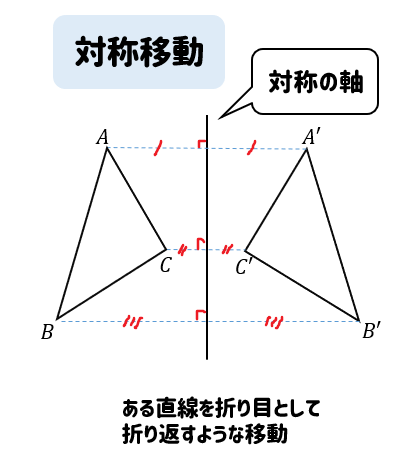
対称移動とは、ある直線を折り目として
パタンと折り返すような移動のことです。
このとき、折り目となった直線のことを対称の軸といいます。
ポイントとしては
それぞれ対応する頂点を結ぶと、対称の軸によって垂直二等分線されているところです。
なので、軸を境に同じ長さ、90°の関係になっています。
対称移動の作図
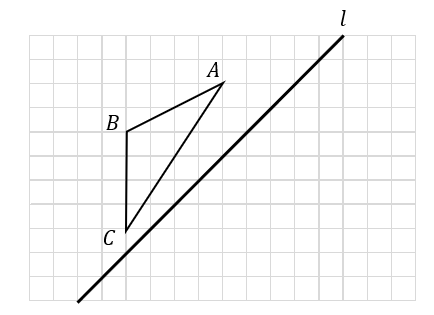
次の図において、△ABCを直線\(l\)について対称移動させた三角形を作図しなさい。
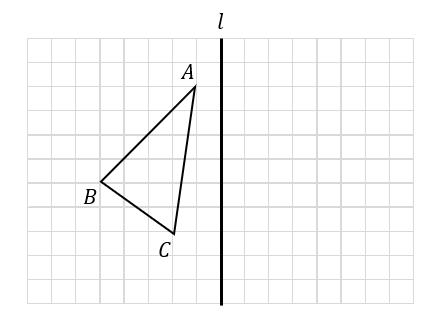
対称移動の作図はとても簡単です!
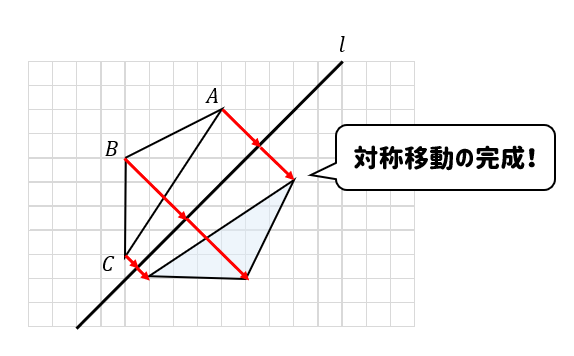
まずは、各頂点から対称の軸に垂線を引いて、どれくらいの長さがあるかを調べます。

そして、次は
軸の反対側に同じ長さだけ動かしたところに点を取ります。
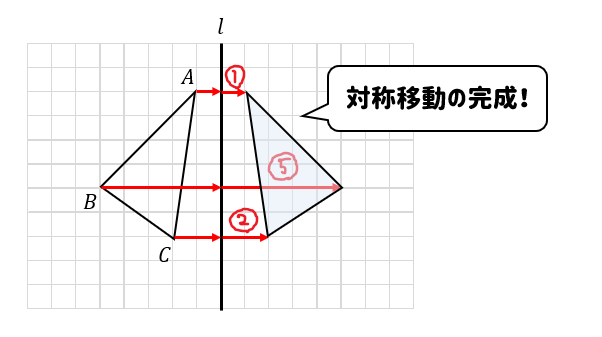
これで対称移動は完成です!
とてもシンプルですね(^^)
次のように図形が軸をまたいでいる場合も考え方は同じ。

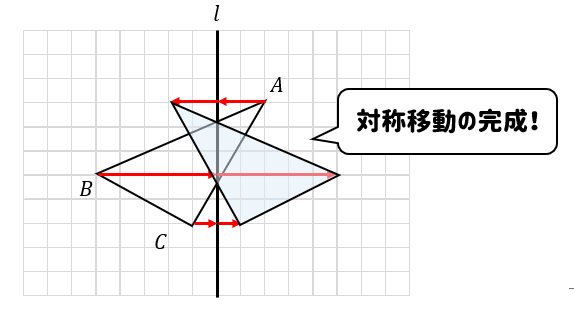
軸が斜めになっている場合には
ヨコとタテの動きに注目すればOKです。
また、対称移動した図形ではなく
対称の軸を作図せよという問題もあります。
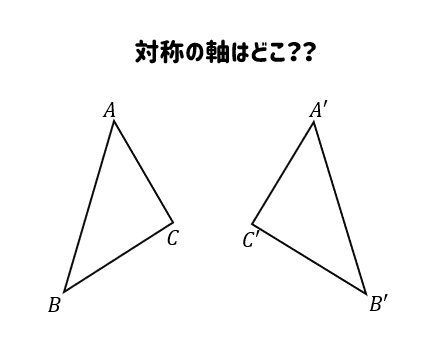
これは「対応する点の垂直二等分線=対象の軸」であることを覚えておけば楽勝です!
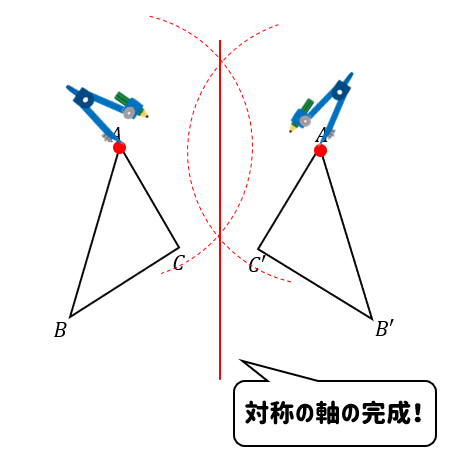
上の図では、点AとA’の垂直二等分線を作図していますが
点BとB’、点CとC’の着目してもOKです。

対称移動して重ねられる図形はどれ?
次の図において、アの図形を対称移動して重ねることができる図形を答えなさい。
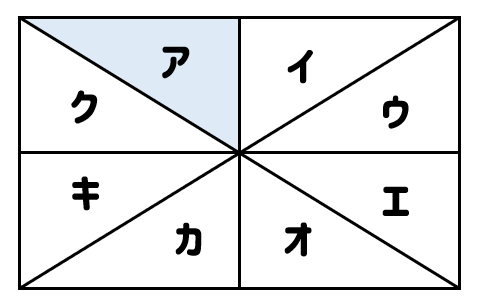
対称移動とは、ある直線を折り目として折り返した移動のことでしたね。
なので、折り返したときに図形アと重なると図形を見つければOKです。
すると、タテの直線を折り目としたとき
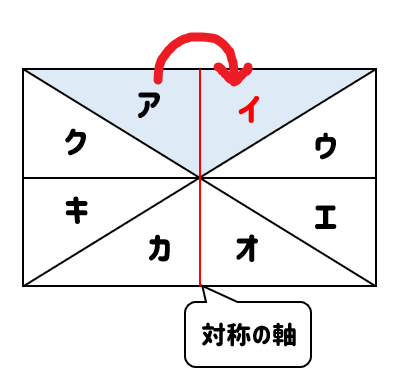
図形イと重なることが分かります。
他にも、ヨコの直線を折り目としたとき
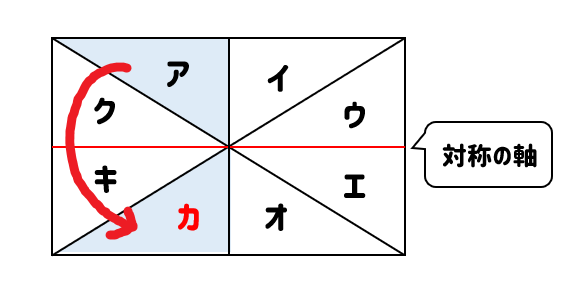
図形カと重なることが分かります。
斜めの線で折ると、図形カに重なるような気もするのですが…
長方形の図形では、斜めに折ったときには重ねることができません。
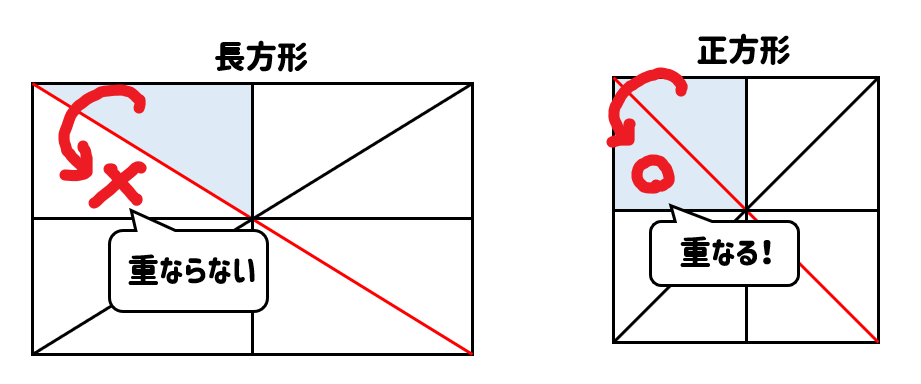
このように、正方形は斜めOK、長方形は斜めNGとなるので間違えないようにしておきましょう。
まとめ!
最後にもう1度、対称移動の特徴を確認しておきましょう!

対称移動とは、ある直線を折り目として折り返すような移動のことをいいます。
このとき、折り目となった直線を対称の軸といいます。
対称移動の作図は簡単!
各頂点から軸に向かって垂線を引き、どれだけ長さがあるかを調べます。
そして、軸の反対側に同じ長さだけいったところに点をとって線で結ぶだけ。
また、対称の軸を作図させる問題では
対応する頂点の垂直二等分線を引けばOKです。
対称移動して重ねられる図形を見つける問題では
いろんな直線で図形折り返してみましょう。
そして、その中からピタッと重なる図形を見つけてください。

















後ろのマスがない場合の解説もしてほしいです。