今回は中2数学で学習する図形と証明の単元から「特別な平行四辺形」について取り上げます。
ここでは「ひし形、長方形、正方形の定義、性質」が問われます。
覚えることが多いですが、問題を解くためのコツを伝授していくのでがんばっていきましょう(‘ω’)ノ
今回の記事を通して、以下の問題をクリアしてもらいます。
平行四辺形ABCDに次の条件を与えると、どんな四角形になるか答えなさい。
(1)\(AB=AD\)
(2)\(∠A=90°\)
(3)\(AB=AD,∠C=90°\)
今回の内容はこちらの動画でも解説しています!
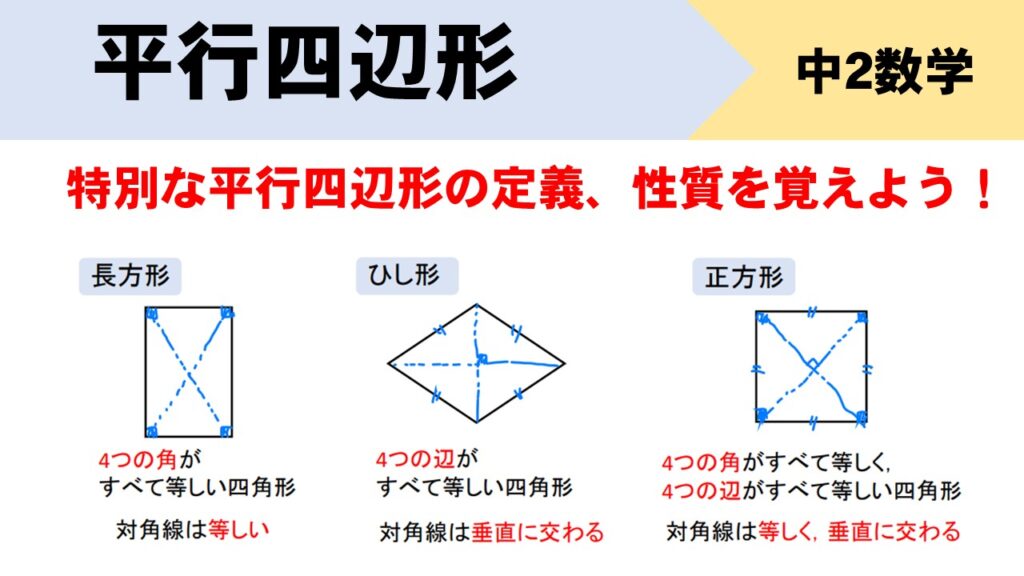
特別な平行四辺形の定義、性質を覚えよう!
これまでに学習してきたように、平行四辺形とは2組の対辺が平行である四角形のことでしたね。
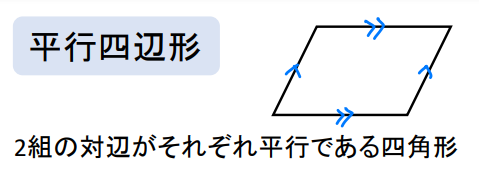
そして、この平行四辺形をもっと細かく分類すると次のようになります。
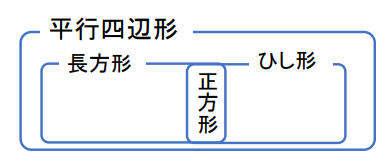
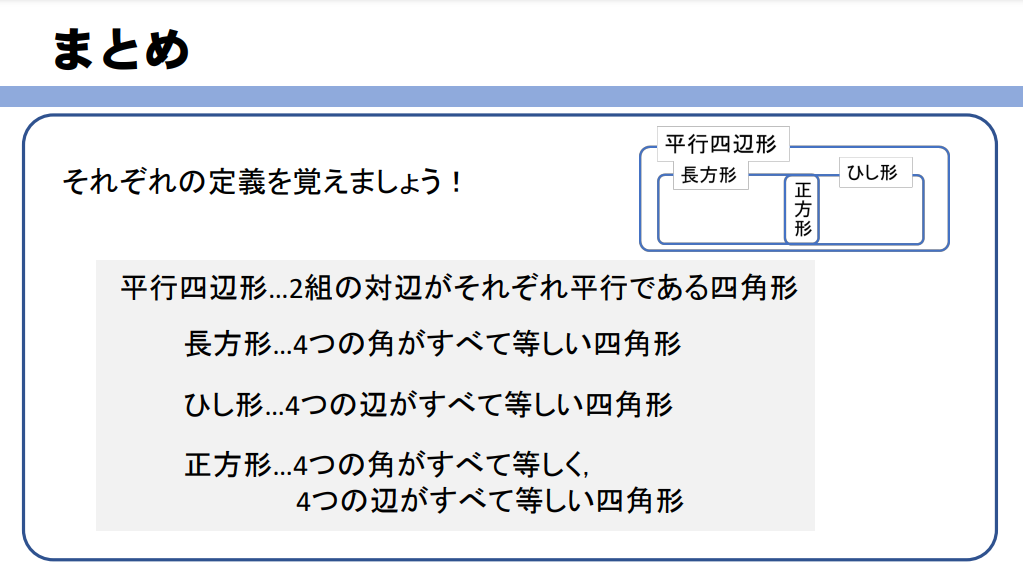
平行四辺形の中には長方形、ひし形があり、その両方の性質を持っている正方形があります。
それぞれの定義、性質は以下の通り!
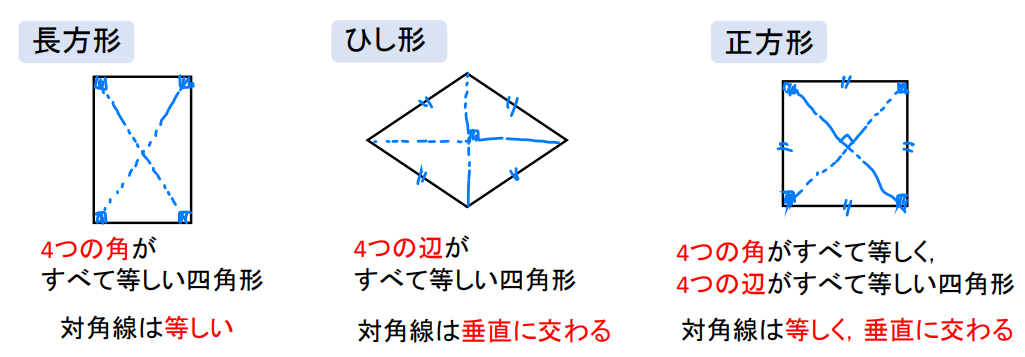
長方形とは4つの角がすべて等しい四角形のことであり、その対角線の長さは等しくなります。
ひし形とは4つの辺がすべて等しい四角形のことであり、その対角線は垂直に交わります。
正方形とは4つの角がすべて等しく、4つの辺がすべて等しい四角形であり、対角線の長さは等しく、垂直に交わります
それぞれの定義だけでなく、対角線の特徴についても問題で問われるので、合わせて覚えておきましょう!
そして、問題を解くためには暗記が必須です。
性質を書き出したり、ノートにまとめるなりして覚えてください。
もうバッチリ覚えれたぞ!という方は、こちらの確認テストにチャレンジしてみましょう(‘◇’)ゞ
【確認テスト】
次の□にあてはまる言葉を答えなさい。
(1)長方形は▢がすべて等しい四角形である、対角線は▢。
(2)ひし形は▢がすべて等しい四角形であり、対角線は▢。
(3)正方形は▢がすべて等しく、▢がすべて等しい四角形であり、対角線は▢。
全問正解できましたか?
完璧だったぜ!という方は次に進みましょう!
どんな四角形になる?変形のコツを伝授!
この単元の問題をクリアするためには、こちらの変形を覚えておきたい。
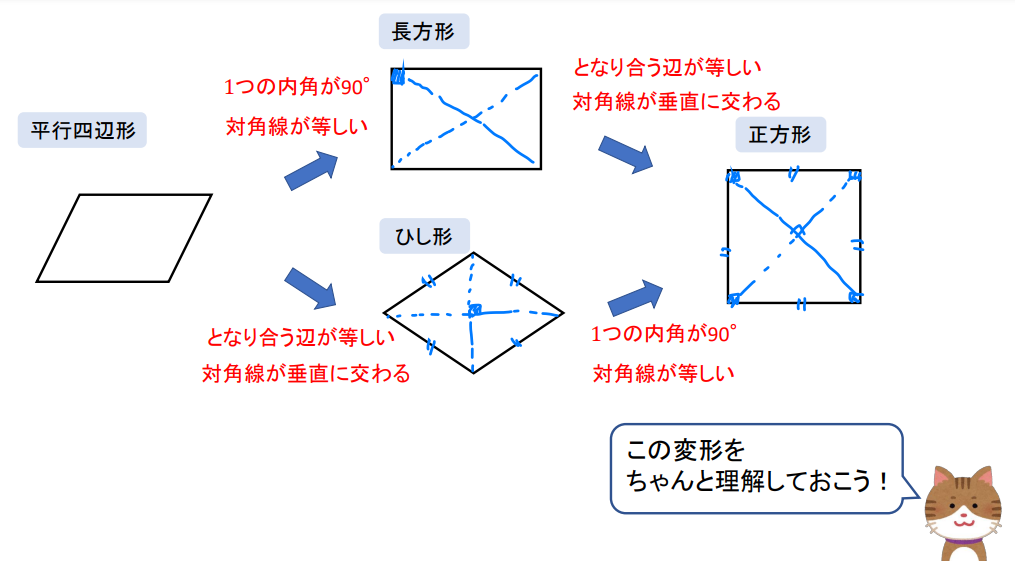
それぞれの図形にどんな特徴を加えて変形するか?というものです。
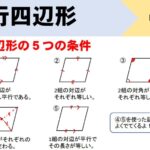
平行四辺形から長方形、ひし形、正方形を作るためには次の変形が必要になります。
長方形…「角が等しい」または「対角線が等しい」
ひし形…「辺が等しい」または「対角線が垂直」
正方形…長方形とひし形の両方の特徴が必要
ここのところは表をパッと見ただけでは理解しづらいかもしれないので、動画解説も参考にしてください!
再生をクリックすると、ちょうど解説部分からスタートします。
演習問題にチャレンジ!
それでは、これまでの学びを活かして次の問題にチャレンジしてみましょう!
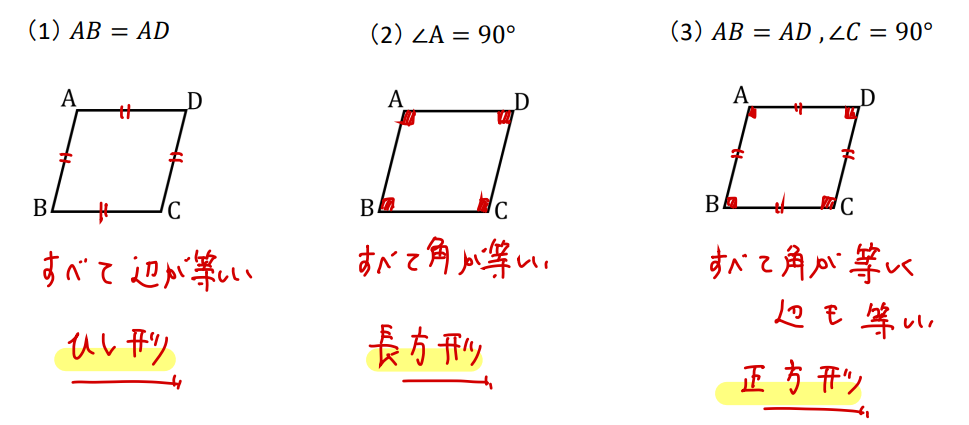
平行四辺形ABCDに次の条件を与えると、どんな四角形になるか答えなさい。
(1)\(AB=AD\)
(2)\(∠A=90°\)
(3)\(AB=AD,∠C=90°\)

まとめ
お疲れ様でした!
問題はバッチリでしたか??
長方形、ひし形、正方形の特徴を覚えてしまえば簡単に解くことができたはず^^
というわけで、最後にそれぞれの図形の特徴をまとめておきますね!















コメントを残す