今回は、数学Ⅰの単元から
「文字係数の一次不等式の解き方」
について解説していきます。
取り上げる問題はこちら!
【問題】(ニューアクションβより)
次の不等式を解け。ただし、\(a\)は定数とする。
(1)\(ax+3<0\)
(2)\((a+1)x≦a^2-1\)
(3)\(ax>b\)
今回の内容は、こちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
文字係数の一次不等式の場合分け
\(x\)の係数が文字になっているときには、次のように場合分けをしていきます。
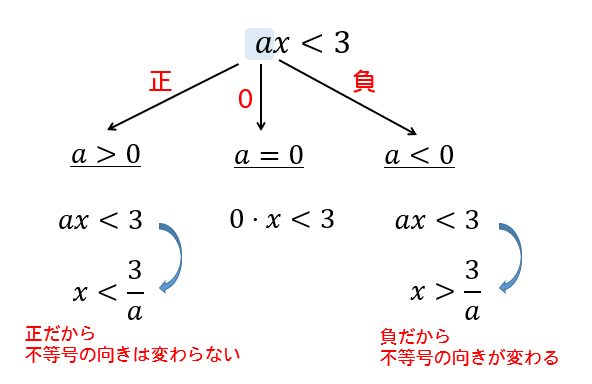
\(x\)の係数が正、0、負のときで場合分けをしていきます。
不等式を解く上で気をつけないといけないこと。
それは、
負の数をかけたり割ったりすると不等号の向きが変わる。
ということですね。
さらに、係数が0になってしまう場合には、
係数で割ってしまうことができなくなります。
\(x\)の係数が文字になっていると、
正?負?それとも0なの?
と、いろんなパターンが考えられるわけです。
なので、全部のパターンを考えて解いていく必要があるのです。
(1)の解説
\(x\)について解いていくと、\(ax<-3\) となる。
ここで、\(x\)の係数である\(a\)が正、0、負のときで場合分けしていきましょう。
\(a>0\)のとき
係数が正なので、不等号の向きは変わりません。
$$\begin{eqnarray}ax&<&-3\\[5pt]x&<&-\frac{3}{a} \end{eqnarray}$$
\(a=0\)のとき
\(0\cdot x<-3\) という不等式ができます。
このとき、左辺は\(x\)にどんな数を入れたとしても0をかけられて0になってしまいます。
どう頑張っても\(-3\)より小さな値にすることはできませんね。
よって、\(x\)にどんな数を入れてもダメ!
つまり、\(a=0\)のときは解なしということになります。
\(a<0\)のとき
係数が負なので、不等号の向きが変わります。
$$\begin{eqnarray}ax&<&-3\\[5pt]x&>&-\frac{3}{a} \end{eqnarray}$$
以上より、解をまとめると
答え
\(a>0\)のとき \(x<-\frac{3}{a}\)
\(a=0\)のとき 解なし
\(a<0\)のとき \(x>-\frac{3}{a}\)
(2)の解説
\(x\)の係数\((a+1)\)が正、0、負のときで場合分けしていきましょう。
\(a+1>0 ⇒ a>-1\)のとき
係数が正になるので、不等号の向きは変わりません。
$$\begin{eqnarray}(a+1)x&≦&a^2-1\\[5pt]x&≦&\frac{a^2-1}{a+1}\\[5pt]x&≦&\frac{(a+1)(a-1)}{a+1}\\[5pt]x&≦&a-1 \end{eqnarray}$$
\(a+1=0 ⇒ a=-1\)のとき
\(0\cdot x≦0\) という不等式ができます。
このとき、\(x\)にどんな値を代入しても左辺は0になります。
すると不等式は、\(0≦0\) となり、ちゃんと成立していることが分かります。
よって、\(x\)がどんな値であっても不等式が成り立つということなので、
\(a=-1\) のとき、解はすべての実数となります。
\(a+1<0 ⇒ a<-1\)のとき
係数が負になるので、不等号の向きは変わります。
$$\begin{eqnarray}(a+1)x&≦&a^2-1\\[5pt]x&≧&\frac{a^2-1}{a+1}\\[5pt]x&≧&\frac{(a+1)(a-1)}{a+1}\\[5pt]x&≧&a-1 \end{eqnarray}$$
以上より、解をまとめると
答え
\(a>-1\)のとき \(x≦a-1\)
\(a=-1\)のとき 解はすべての実数
\(a<-1\)のとき \(x≧a-1\)
(3)の解説
ん、これって簡単じゃない?
と思った方はちょっと落とし穴にはまっているかもしれませんw
この問題は2段階の場合分けが必要になります。
まずは、\(x\)の係数\(a\)が正、0、負のときで場合分けしていきましょう。
\(a>0\)のとき
係数が正になるので、不等号の向きは変わりません。
$$\begin{eqnarray}ax&>&b\\[5pt]x&>&\frac{b}{a} \end{eqnarray}$$
\(a<0\)のとき
係数が負になるので、不等号の向きが変わります。
$$\begin{eqnarray}ax&>&b\\[5pt]x&<&\frac{b}{a} \end{eqnarray}$$
ここまでは簡単ですね!
気を付けるのは次、係数が0になるときのパターンです。
\(a=0\)のとき
\(0\cdot x>b\) という不等式ができます。
ここで困ったことが起こります。
\(x\)がどんな数であっても左辺は0になります。
ですが、\(b\)の値が分からんから、
\(0>b\)が成立するのかどうか不明!
ということになります。困りますね(^^;)
なので、ここからさらに場合分けをしていきます。
\(b<0\) であれば、\(0>b\) が成立することになるので、
解はすべての実数ということになります。
\(b≧0\) であれば、\(0>b\) は成立しないので、
解なしということになります。
以上のことをまとめると、
答え
\(a>0\)のとき \(x>\frac{b}{a}\)
\(a=0\)のとき \(b<0\)ならば解はすべての実数、\(b≧0\)ならば解なし
\(a<0\)のとき \(x<\frac{b}{a}\)
まとめ!
お疲れ様でした!
最後の問題はちょっと複雑な感じでしたが、
係数が文字になっている場合には次のようなイメージを持っておくようにしましょう!
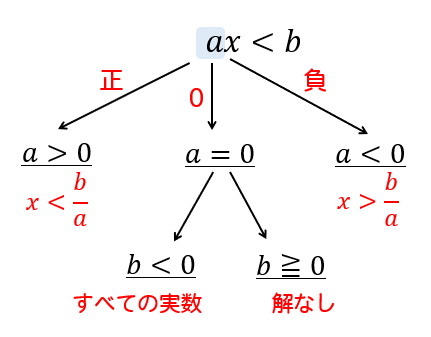

















(1)のa<0のとき、a分の3にならないのはなぜですか?なぜマイナスの符号がつくのか教えてください
a<0 だからといって
-aにするわけではなく
aの中身が負の数になるだけだからです!