今回は高校数学Ⅱで学習する円の方程式から
『円の接線の方程式』
について解説していきます。
円の接線公式は、とっても簡単なものだからサクッとマスターしておきましょう(^^)
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
円の接線公式
円の接線公式は以下の2つを覚えておきましょう。
\(x^2+y^2=r^2\)上の点\((x_1, y_1)\)における接線
$$\large{x_1x+y_1y=r^2}$$
\((x-a)^2+(y-b)^2=r^2\)上の点\((x_1, y_1)\)における接線
$$(x_1-a)(x-a)+(y_1-b)(y-b)=r^2$$
数式で見ると難しそうに見えちゃうので例題を使って説明します。

こんな感じです!簡単だね。
まず、\(x,y\)を分ける。
分けた\(x,y\)の1つに接線の座標を入れる。
完成!
こちらの公式も同様です。

まず、\(x,y\)のかたまりを分ける。
分けた\(x,y\)のかたまりの1つに接線の座標を入れる。
完成!
円の接線を公式通り覚えようとすると難しいです。
このように例題を通して身につけてしまえば、とっても簡単だって分かりますね(^^)
それでは、次は円の接線公式を用いてちょっとした応用問題に挑戦してみよう。
円外の点から引いた接線の方程式
ん?簡単じゃん!
公式を使って
$$\large{3x+y=5}$$
こうすればいいんじゃないの?
と、したくなるとことなんだけど
引っかからないでください!!
もしも\((3,1)\)という点が、円上にある接点であれば公式を使って、そのように解くことができます。
しかし、今回の問題では\((3,1)\)は接点ではなく、円外にある点です。
だから、公式を使って簡単に解くことができないのです…
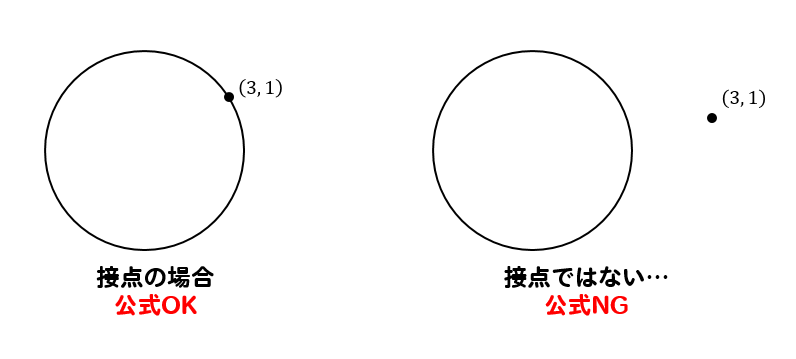
という訳で、今回の問題のように接点が分からない場合には困ってしまうのです。
接点がなくて困る…
それならば、接点を作ればいい!!
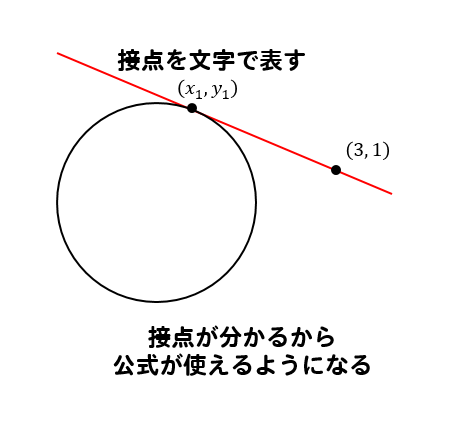
ってな感じで、接点を文字で置いてやることで接線の式を作っていきます。
接点を作ってあげたことで、2つの良いことがあります。
まず1つ目は、文字を使って接線の式を作れること。
\(x^2+y^2=5\)上の点\((x_1, y_1)\)における接線
$$\large{x_1x+y_1y=5}$$
更に、この接線は\((3,1)\)を通るのだから
$$\large{3x_1+y_1=5}$$
と表せます。
2つ目は、接点は円上にある点だから円の方程式に代入できる。
$$\large{x_1^2+y_1^2=5}$$
と、このように2つの式を作ることができます。
あとは、この2つの式を連立方程式で解いて\(x_1, y_1\)の値をそれぞれ求めます。
連立方程式は代入法で解くのがいいですね。
\(3x_1+y_1=5\)を\(y_1=5-3x_1\)に変形し
\(x_1^2+y_1^2=5\)に代入します。
$$x_1^2+(5-3x_1)^2=5$$
$$x_1^2-3x_1+2=0$$
$$(x_1-1)(x_1-2)=0$$
$$x_1=1,2$$
\(x_1=1\)のとき
$$y_1=5-3\times 1=2$$
\(x_1=2\)のとき
$$y_1=5-3\times 2=-1$$
以上より、接点は\((1,2)\)、\((2,-1)\)の2つあることが分かります。
よって、求めたい接線の方程式は
$$x+2y=5$$
$$2x-y=5$$
の2つであることが分かりました。
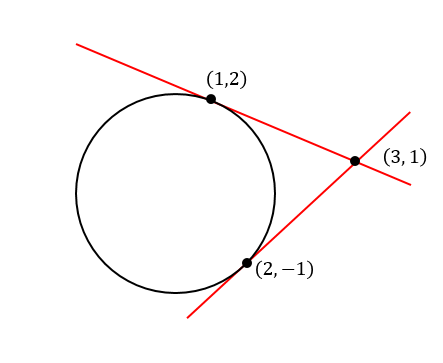
今回の問題のように、問題で接点を与えられない場合
文字で接点を表してあげることがポイントです。
そうしてあげることで、文字を使って式を作ることができます。
あとは連立方程式を解いて、値を明らかにしていきましょう。
まとめ
お疲れ様でした!
接点が分かっている場合の問題は超簡単でした。
これはテストに出題された場合、しっかりと得点源にしておきたいラッキー問題だね!
それに対して、接点が分からない場合の問題はちょっと難易度が高い…
それだけにテストでは配点も高めに設定されていることがあるから、しっかりと解けるようにしておけば点数アップ間違いなしだ!
たくさん練習して、マスターしておこうね(/・ω・)/

















コメントを残す