こんにちは!数スタの小田です。
今回は高校数学Aで学習する図形の単元から「円に内接する四角形の角度」について取り上げます。
(高校入試にも出てくることがある問題ですね)
とっても簡単な問題なので、しっかりと理解してテストで得点できるようにしましょう^^
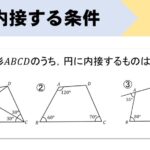
【問題】
次の図において、角\(\theta\)を求めなさい。
サクッと理解したい方は、こちらの動画も参考にしてください!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
円に内接する四角形の特徴
この2つの特徴をしっかりとおさえておきましょう!
では、これを頭に入れた上で各問題の解き方をチェックしていきます。
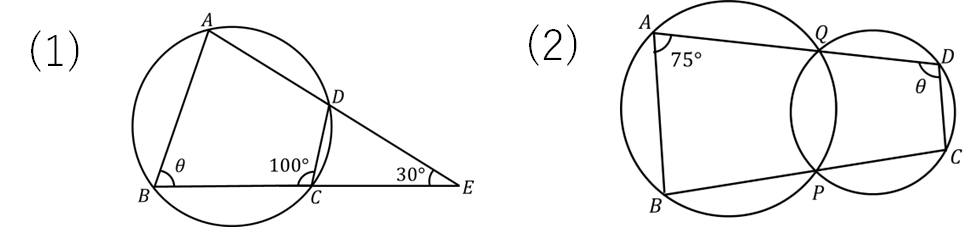
(1)の解説
いろいろな着眼点がありますが、僕は次のように考えました。

まずは赤色の内接する四角形に注目して、\(\theta\)の角をDのところに持っていきました。
次に青色の三角形に注目して、三角形の外角の性質を使って計算しています。
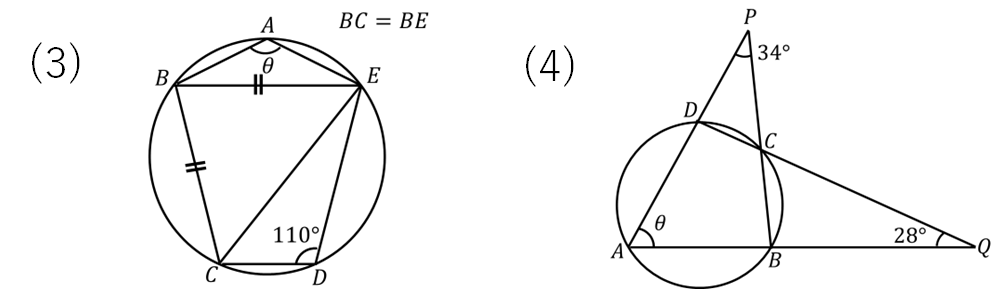
(2)の解説
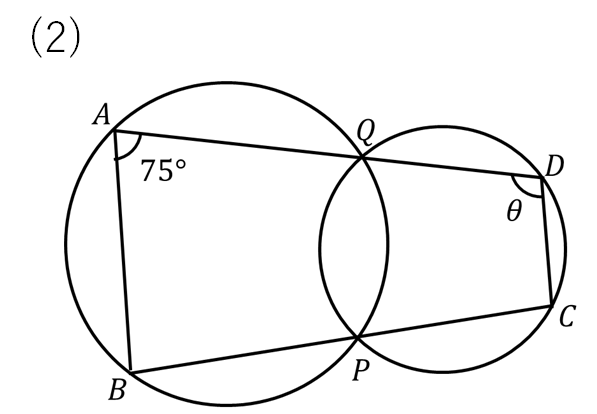
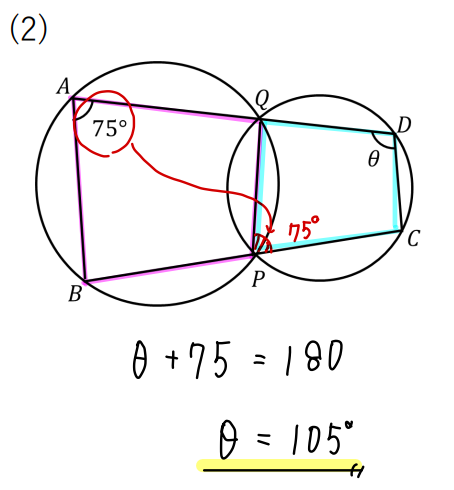
まずはQPに補助線を入れます。(←これが大事なポイントですね!)
そして、赤色の内接する四角形から75°を動かす。
次に、青色の内接する四角形の対角の和が180°になることを使って計算します。
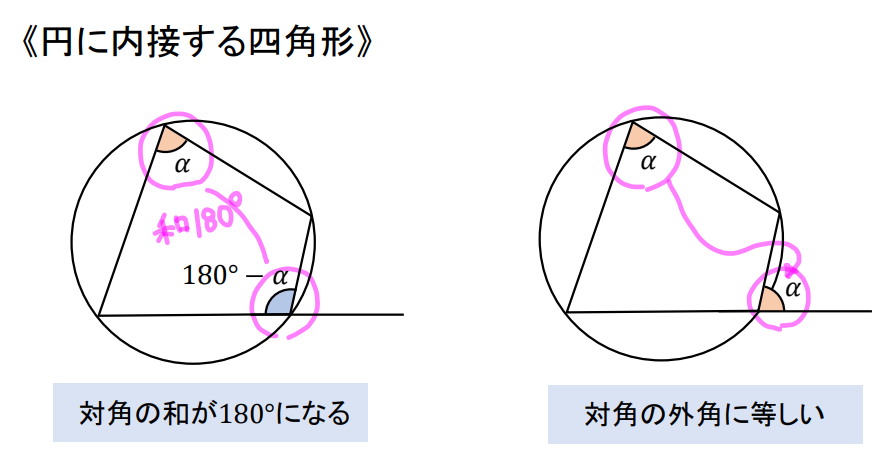
(3)の解説
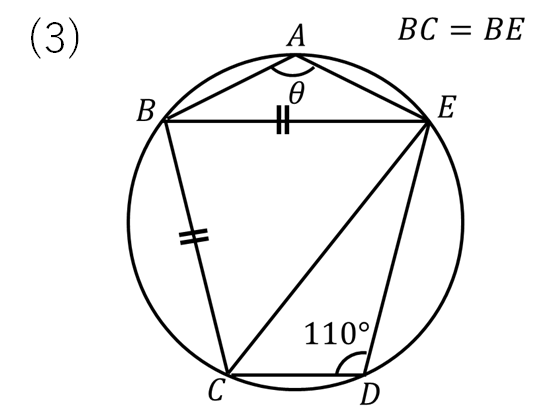
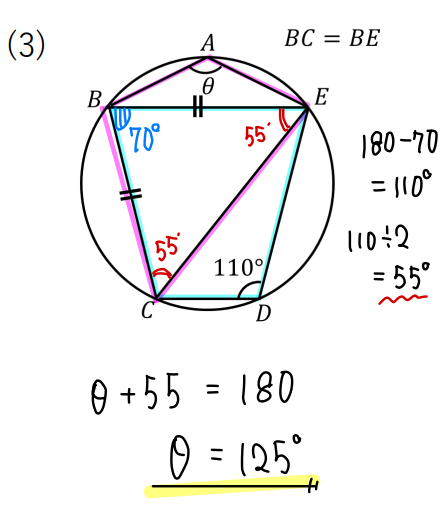
まずは青色の内接する四角形から、110°の対角にある70°の角を書き込みます。
次に△BCEが二等辺三角形であることより、底角55°を求めましょう。
最後に赤色の内接する四角形より、55°と\(\theta\)が対角の位置にあるので、和が180°になることを使って計算します。
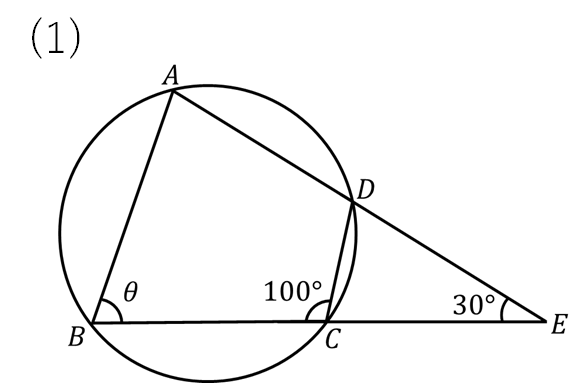
(4)の解説
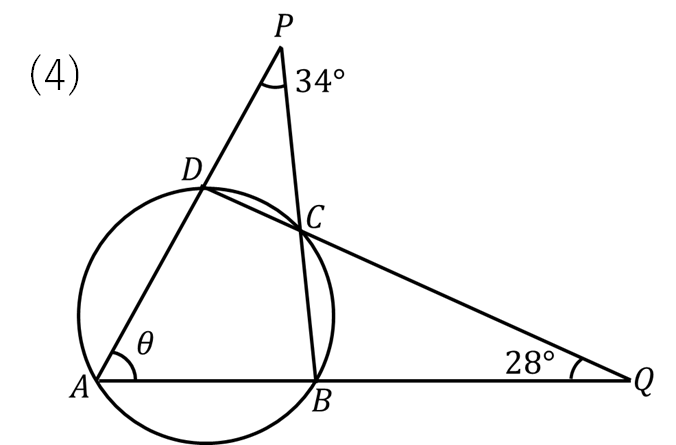
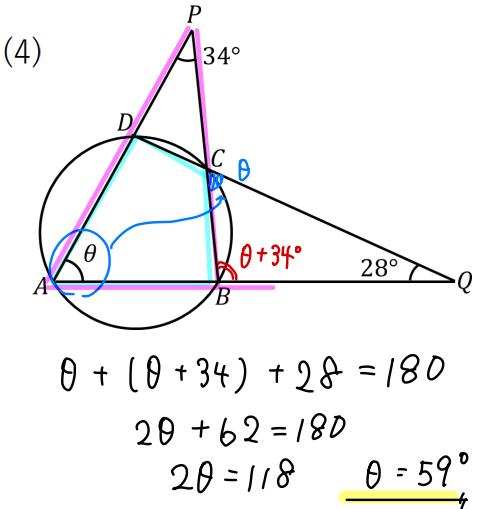
青色の内接する四角形より、\(\theta\)をCのところに動かす。
赤色の三角形の外角より、Bのところが\(\theta + 34°\)となります。
△CBQに注目すると、3つの内角がそれぞれ\(\theta, \theta+34°, 28°\) と表すことができました。内角の和は180°であることより、方程式をつくって\(\theta\)を求めます。
この問題はちょっとややこしいですね(^^;)
文章の解説だけではよくわからんかった…という方は、こちらの動画解説も参考にしてください!
(再生を押すとこの問題の解説からスタートします)
円に内接する平行四辺形の角
最後はちょっと小ネタのような問題を取り上げて終わりにしたいと思います!
【問題】
円に内接する平行四辺形の4つの内角の大きさを求めなさい。
動画解説はこちら!
ここでは「平行四辺形の性質」「円に内接する四角形の性質」をコラボさせて考えていきます。
平行四辺形ということは ⇒ 対角の大きさが等しい
円に内接するということは ⇒ 対角の和が180°になる
ということで、今回取り上げている平行四辺形は
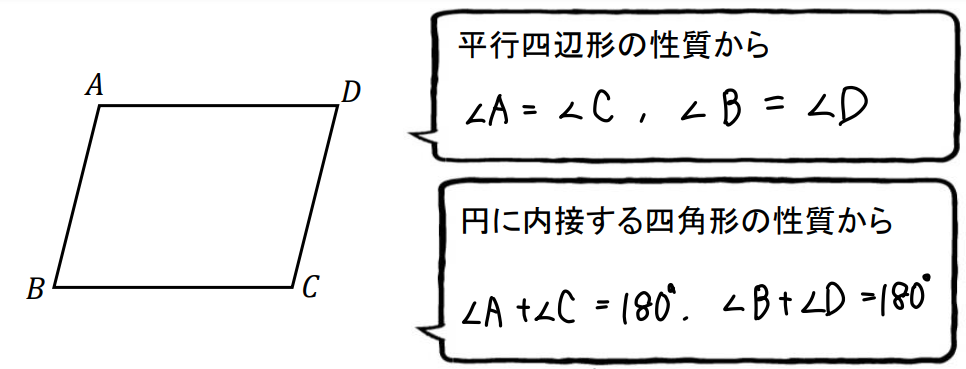
このような関係が成り立つことがわかります。
\(∠A=∠C、∠A+∠C=180°\) より、代入して計算してみると
$$\begin{eqnarray}∠A+∠A&=&180°\\[5pt]2∠A&=&180°\\[5pt]∠A&=&90° \\[5pt]∠A=∠Cより,∠C&=&90°\end{eqnarray}$$
∠B、∠Dも同様に計算すると、\(∠B=∠C=90°\)となります。
よって、円に内接する平行四辺形の内角はすべて90°になるとわかりますね!
答え
すべて90°になる
というわけで、小ネタの平行四辺形についてでした!
テストに出てくるかもしれませんので、考え方をちゃんと覚えておいてくださいね^^
では、円に内接する四角形の角度については以上!
あとは学校のワークを使っていろんなパターンを演習しておきましょう(‘ω’)ノ












コメントを残す