今回の記事では高校数学Ⅰでデータの分析を学習している方に向けて
「共分散とは何か?」
について簡単に解説していきます。
共分散とはなにか、求め方は?
2つの変量について考えるとき
この2つのデータにはどんな関係性があるんだろう?
というのを考えます。
例えば次のようなデータです。
| Aくん | Bくん | Cさん | Dくん | Eさん | |
| 数学 | 5点 | 3点 | 8点 | 4点 | 1点 |
| 英語 | 4点 | 2点 | 9点 | 8点 | 3点 |
データの関係性については、散布図と呼ばれる図を描いてみると見た目で分かりやすくなります。
散布図とは次のような図のことで、グラフの座標をとるようにデータを置いていきます。
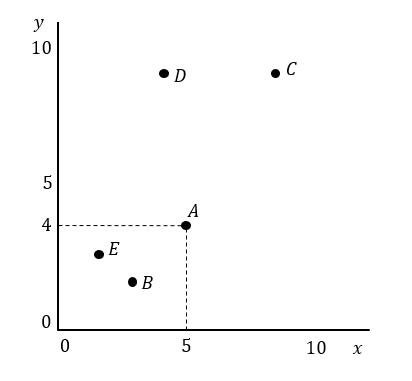
こうやって散布図を作ったとき
データの配置が右上がりの直線のように、一方が増加すると他方も増加する場合
2つの変量には正の相関があるといいます。
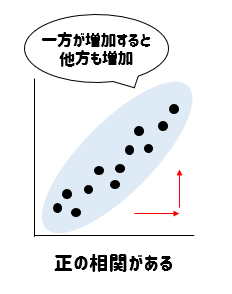
データの配置が右下がりの直線のように、一方が増加すると他方も減少する場合
2つの変量には負の相関があるといいます。
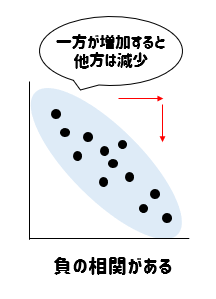
上の2つのどちらでもない場合、つまりデータが散らばっていて特徴が見られないとき
2つの変量には相関がないといいます。
以上のように、散布図を書くことでデータの特徴(相関)を調べることができるのですが…
データの数が多くなると散布図を作るのが大変ですね(^^;)
散布図を書くことなくデータの相関を調べることはできないものか。
ということで活用されるのが共分散(きょうぶんさん)というものです。
共分散とは、変量\(x\)の偏差と変量\(y\)の偏差をかけたものの平均です。
共分散の求め方
$$s_{xy}=\frac{1}{n}\{(x_1-\overline{x})(y_1-\overline{y})+\cdots +(x_n-\overline{x})(y_n-\overline{y})\}$$
共分散が正 ⇒ 正の相関がある
共分散が負 ⇒ 負の相関がある
んー、これだけをお伝えすると難しく感じちゃいますのでもう少しかみ砕いて説明しますね。
\(x,y\)の平均を中心に考えた場合
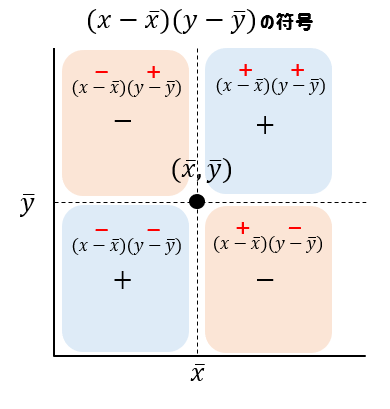
\((x-\overline{x})(y-\overline{y})\)が+になるときには右上、左下のどちらかに配置されることが分かります。
\((x-\overline{x})(y-\overline{y})\)が-になるときには右下、左上のどちらかに配置されることが分かります。
つまり
\((x-\overline{x})(y-\overline{y})\)を調べたときに+になるものが多ければ、右上がりの直線のような形になる。つまり、正の相関がある。
\((x-\overline{x})(y-\overline{y})\)を調べたときに-になるものが多ければ、右下がりの直線のような形になる。つまり、負の相関がある。
ということが分かるのです。
そこで、\((x-\overline{x})(y-\overline{y})\)の平均をとることでデータ全体の傾向をつかもうということです。
そして、\((x-\overline{x})(y-\overline{y})\)の平均の値のことを共分散といいます。
次の章では、共分散を値をイチから求めてみましょう。
共分散の求め方をイチから
次のデータの共分散を求めなさい。
| A | B | C | D | E | |
| 数学 | 8 | 9 | 6 | 2 | 10 |
| 英語 | 2 | 2 | 5 | 5 | 6 |
数学の変量を\(x\)、英語の変量を\(y\)として話を進めます。
まずは数学、英語の平均をそれぞれ求めましょう。
$$\begin{eqnarray}\overline{x}=\frac{8+9+6+2+10}{5}=7 \end{eqnarray}$$
$$\begin{eqnarray}\overline{y}=\frac{2+2+5+5+6}{5}=4 \end{eqnarray}$$
平均が求まったらそれぞれの偏差を求め、\(x,y\)の偏差をかけたものを求めます。
慣れるまでは次のような表を作ると良いですよ。
| 数学\(x\) | 英語\(y\) | \(① x-\overline{x}\) | \(② y-\overline{y}\) | \(①\times②\) | |
| A | 8 | 2 | 1 | -2 | -2 |
| B | 9 | 2 | 2 | -2 | -4 |
| C | 6 | 5 | -1 | 1 | -1 |
| D | 2 | 5 | -5 | 1 | -5 |
| E | 10 | 6 | 3 | 2 | 6 |
| 計 | 35 | 30 | \(\color{red}{-6}\) |
それぞれの偏差をかけたものの和(赤字になっている数)が求まったら、それを個数で割れば共分散の完成となります。
$$\frac{-6}{5}=-1.2\cdots(解)$$
つまり、今回のデータには負の相関があるということが分かりますね。
まとめ!
共分散の求め方
※数式が切れている場合、横にスライドできます。
共分散が正 ⇒ 正の相関がある
共分散が負 ⇒ 負の相関がある
共分散とは、2つのデータにどういった相関があるのかを判断するためにそれぞれの偏差をかけて考えたものでした。
共分散が求めれるようになったら、次は相関係数について考えてみましょう!
















高3生です。
ずっと分からなかった共分散をスっと理解できました!
もっと早く見ておけば良かった……と思うくらい感動してます!
ありがとうございました
お役に立ててよかったです!
受験勉強がんばってくださいね^^