今回は高校数学Ⅰでデータの分析を学習している方に向けて
「分散の求め方」
についてイチから解説していきます。
そもそも分散って何?っていうことを理解するのが大事!
サクッと理解したい方は、こちらの動画も参考にしてください!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
分散となにか?求め方は?
データがどれくらい散らばっているかを表したものを分散といいます。
じゃぁ、ここからはちょっとストーリー仕立てで説明していきますね。
ある人は
「どうやったらデータの散らばり度合いを表せるか」ということを考えていました。
そうだ!
それぞれのデータが平均からどれくらい離れているかを考えればよいのでは!?
平均から離れているデータが多ければ散らばっている。
平均の近くにデータが多ければ散らばっていない。
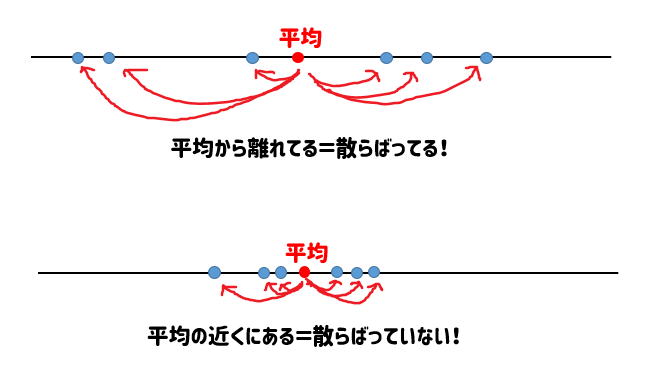
そこで、それぞれのデータが平均からどれくらい離れているかに着目しました。
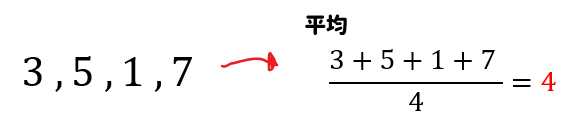
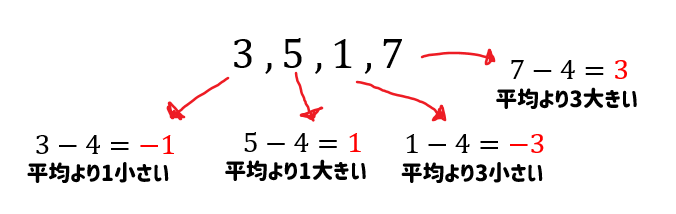
このように、平均よりどれくらい大きいか、小さいかを表した値のことを偏差(へんさ)といいます。
よし!
平均からの散らばり具合をそれぞれ表せたから
これらの平均をとれば、全体の散らばり具合を表せたことになるのではないか!
そう考えて、偏差の平均をとってみることにしました。
すると…
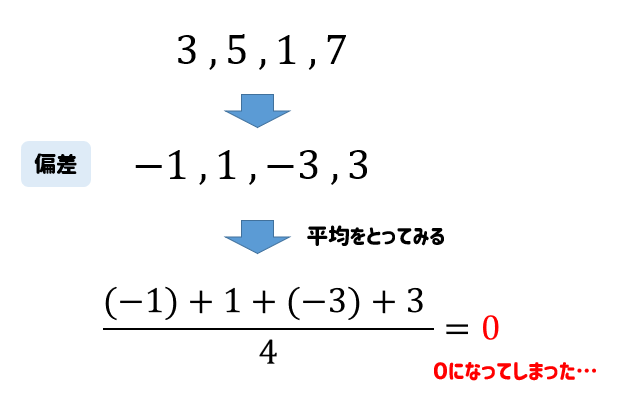
なんと、偏差の平均は0になってしまいました。
これはどんなデータでやってみても必ず0になってしまいます。
これでは、散らばり度合いを表す数値としては役に立たないではないか。
困ってしまいました。
んー
だったら偏差を2乗してしまえ!
2乗しても散らばりを表す数値には違いない!
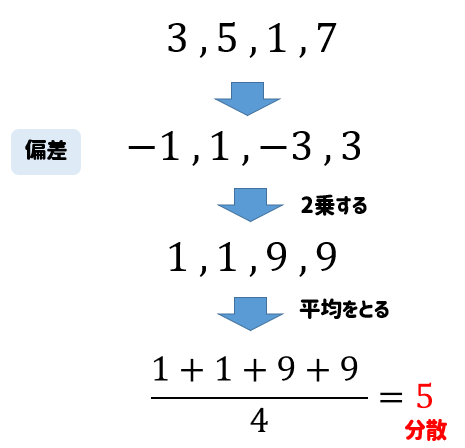
というわけで、偏差の2乗の平均を求めることでデータ全体の散らばり度合いを表す数値としたのです。
この数値のことを分散といいます。
分散の求め方については次のストーリー展開で覚えておくと、忘れにくいのでおススメです(^^)
- 散らばり度合いは平均からどれくらい離れているか(偏差)を考えればいいっしょ!
- 偏差の平均を求めたら0になっちまうぜ…困った。
- そうだ!偏差を2乗してしまえ!
- 偏差を2乗した値の平均が分散だぜ
もうすこし数学っぽくまとめておくと次のようになります。
分散の求め方
変量\(x\)についてのデータの値が\(x_1,x_2\cdots,x_n\)、平均値が\(\overline{ x }\)のとき
※数式が切れている場合はヨコにスライドできます。
ちなみに、分散にルートをつけたものを標準偏差といいます。
標準偏差の求め方
$$【標準偏差】s=\sqrt{分散}$$
分散の求め方をイチから
次のデータは小テストを行った結果です。このデータの分散と標準偏差を求めなさい。
$$5,8,6,4,2(点)$$
まずは平均を求めしょう。
$$\overline{ x }=\frac{5+8+6+4+2}{5}=5(点)$$
平均が求まったら偏差、偏差の2乗を求めましょう。
慣れるまでは次のように表を作って考えるといいですね。
| $$x$$ | $$5$$ | $$8$$ | $$6$$ | $$4$$ | $$2$$ |
| $$x-\overline{ x }$$ | $$0$$ | $$3$$ | $$1$$ | $$-1$$ | $$-3$$ |
| $$(x-\overline{ x })^2$$ | $$0$$ | $$9$$ | $$1$$ | $$1$$ | $$9$$ |
最後に、偏差の2乗の平均をとれば分散の完成です!
$$\frac{0+9+1+1+9}{5}=\color{red}{4}\cdots(解)$$
ちなみに、分散には単位をつけません。
そして、分散が求まったら標準偏差を求めましょう。
標準偏差は分散にルートをつけるだけです。
$$\sqrt{4}=\color{red}{2(点)}\cdots(解)$$
標準偏差には単位をつけます。
答え
$$【分散】4$$
$$【標準偏差】2(点)$$
手順を覚えてしまえば簡単に求めることができますね(^^)
もう1つの分散求め方
実は分散の求め方にはもう1つのやり方があります。
それがコレ!
分散の求め方
$$s^2=\overline{ x^2 }-\overline{ x }^2$$
(2乗の平均)引く(平均の2乗)
なぜこのような公式で分散が求めれるかについては
こちらの記事をご参考ください。
この公式の使いどころっていうのは
偏差が小数になっちゃうとき
です。
偏差が小数になっちゃうと、偏差の2乗なんて計算していたら値がとんでもないことになっちゃいますね(^^;)
計算が複雑すぎてやってられない!
そういうときには上で紹介したもう1つの求め方を利用します。
具体例として、さっきのデータを使って求めてみますね。
次のデータは小テストを行った結果です。このデータの分散を求めなさい。
$$5,8,6,4,2(点)$$
まずはそれぞれのデータを2乗した値を作ります。
| $$x$$ | $$5$$ | $$8$$ | $$6$$ | $$4$$ | $$2$$ |
| $$x^2$$ | $$25$$ | $$64$$ | $$36$$ | $$16$$ | $$4$$ |
そして、そのままのデータの平均と2乗したデータの平均を求めます。
$$\overline{ x }=\frac{5+8+6+4+2}{5}=5$$
$$\overline{ x^2 }=\frac{25+64+36+16+4}{5}=29$$
そして、これらの値を\(\overline{ x^2 }-\overline{ x }^2\) に当てはめて計算すると分散が求まります。
$$\begin{eqnarray}s^2&=&\overline{ x^2 }-\overline{ x }^2\\[5pt]&=&29-5^2\\[5pt]&=&4\cdots(解) \end{eqnarray}$$
と、まぁこんな感じで求めることができます。
偏差が複雑な値になってしまうときには、このやり方で分散を求めるようにしましょう。
公式をそのまま式で覚えるのはちょっと難しいので
(2乗の平均)引く(平均の2乗)
という言葉で理解しておくと覚えやすいですよ(^^)
xと2x+3の分散はどう違う?
ここからはちょっと発展的な内容になりますが、入試レベルの問題を解くためにはしっかりと頭に入れておきたいです。
変量\(x\)と変量\(2x+3\)の分散にはそれぞれどのような違いがあるのか。
これについて簡単にお話をしておきます。
結論からいうと
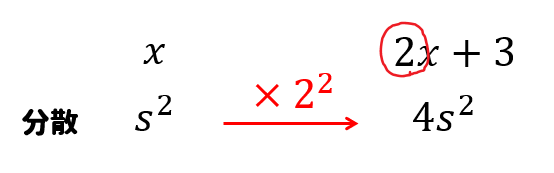
このような関係になっています。
元の変量\(x\)に2倍して3を加えてできた変量\(2x+3\)の分散は、\(x\)の分散に対して\(\times 2^2\)となります。
加えたり引いたりという値は完全に無視して、何倍されたかの値に注目します。
その何倍されたかの値を2乗したもの。
それが分散の違いになります。
その理由については次のような式変形で示すことができます。
字が汚くてごめんなさい…(^^;)
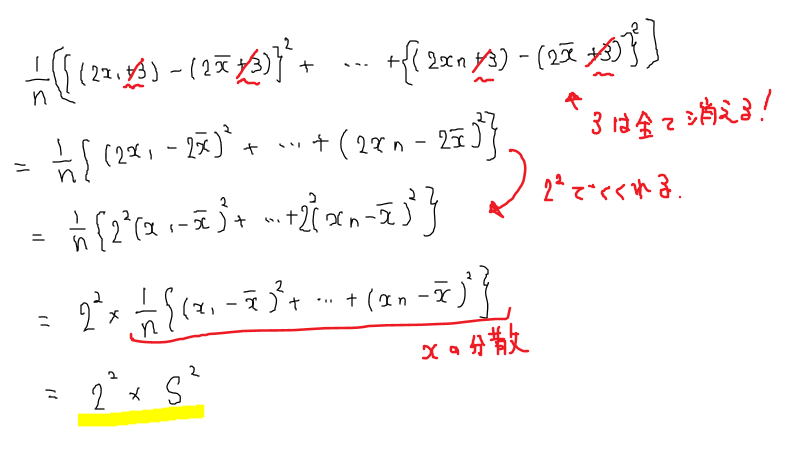
これを見ると分かるように、加えたり引いたりする値というのは分散を求める過程で消えてしまいます。
そして、何倍したかという値が2乗されてくくりだされるということが分かりますね。
ちなみに、標準偏差の場合にはそのまま何倍の形になります。
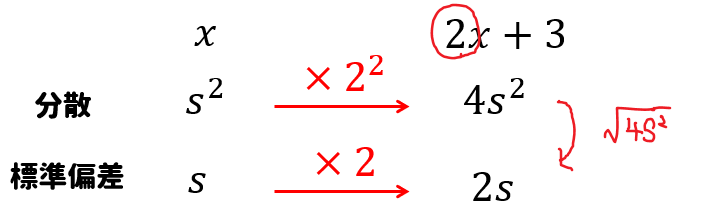
まぁ、標準偏差は分散にルートをつけたものだから
分散の値がどうなるかを理解していればすぐに分かりますね!
【例題】
変量\(x\)に対して、\(y=\frac{x-3}{2}\)とする。
変量\(x\)の分散を\(s_x^2\)、変量\(y\)の分散を\(s_y^2\)とするとき
\(\frac{s_y^2}{s_x^2}\)の値を求めなさい。
変量\(y\)は次のように変形できます。
$$y=\frac{1}{2}x-\frac{3}{2}$$
\(\frac{1}{2}\)倍されているということが読み取れます。
つまり、分散\(s_y^2\)は\(s_x^2\)に対して\(\left(\frac{1}{2}\right)^2\)倍されているということになります。
よって、\(s_y^2=\frac{1}{4}s_x^2\)となります。
以上より
$$\frac{s_y^2}{s_x^2}=\frac{\frac{1}{4}s_x^2}{s_x^2}=\frac{1}{4}\cdots(解)$$
となります。
ポイントは、\(y\)が\(x\)の何倍になっているかを読み取れること。
足したり引いたりっていう\(-\frac{3}{2}\)の部分は分散の値には関係しないので無視するってことですね。
まとめ!
お疲れ様でした。
今回の内容は数式が多くて大変だったと思いますが
ここまでたどり着いた読者の方は素晴らしい粘り強さだと思います(^^)
公式の形だけ見ると、すごく複雑に思えますね(^^;)
だけど、冒頭で紹介したようにストーリー仕立てで分散の求め方を理解しておくと忘れにくいし、式の意味も理解できるようになるのでおススメです。
まぁ、あとはたくさん練習問題に挑戦して
どれだけ体に覚えこませるかが大事です。
分散をマスターするためには、とにかく手を動かすべし!
ファイトだ(/・ω・)/















コメントを残す