今回の記事では、高校数学で学習する
微分のやり方
についてまとめていきます。
数学Ⅱで学習する微分、更には数学Ⅲで学習する微分まで
計算方法を簡単にまとめておきます。
基本計算についてはこちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
【微分のやり方】導関数の定義
関数\(f(x)\)の導関数\(f'(x)\)は、次のように求めることができます。
このように導関数を求めることを微分するといいます。
導関数の定義に従って微分をすると以下のようになります。
次の関数を微分しなさい。
$$f(x)=2x^2$$
$$\begin{eqnarray}f'(x)&=&\lim_{ h \to +0 }\frac{f(x+h)-f(x)}{h} \\[5pt]&=&\lim_{ h \to +0 }\frac{2(x+h)^2-2x^2}{h}\\[5pt]&=&\lim_{ h \to +0 }\frac{2x^2+4hx+2h^2-2x^2}{h}\\[5pt]&=&\lim_{ h \to +0 }(4x+2h)\\[5pt]&=&4x\end{eqnarray}$$
このような計算式になります。
ちょっとメンドイですね(^^;)
だけど、大丈夫!
こんな定義を使わなくても、簡単に微分をやる方法がありましたね。
なので、微分をするという問題では、基本的には簡単なやり方を使っていくことになります。
【微分のやり方】導関数の公式
導関数の公式
- \(y=c\) ならば、\(y’=0\)
- \(y=x^n\) ならば、\(y’=nx^{n-1}\)
- \(y=kf(x)\) ならば、\(y’=kf'(x)\)
- \(y=f(x)+g(x)\) ならば、\(y’=f'(x)+g'(x)\)
これらの公式を使うと、簡単に微分をすることができます。
例えば、先ほど取り上げた \(f(x)=2x^2\)を公式に従って微分をすると
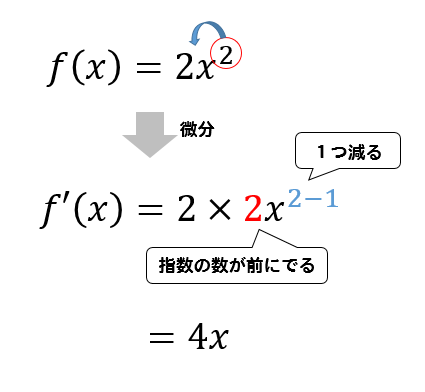
となります。
めっちゃめちゃ簡単ですね!
いくつか具体例を挙げておきます。
次の関数を微分しなさい。
$$f(x)=4x^2-3x+1$$
$$\begin{eqnarray}f'(x)&=&(4x^2)’-(3x)’+(1)’\\[5pt]&=&8x-3 \end{eqnarray}$$
次の関数を微分しなさい。
$$f(x)=(x-3)^2$$
まずは式を展開してやります。
$$f(x)=(x-3)^2=x^2-6x+9$$
展開できたら、ここから微分スタート!
$$\begin{eqnarray}f'(x)&=&(x^2)’-(6x)’+(9)’\\[5pt]&=&2x-6 \end{eqnarray}$$
次の関数を微分しなさい。
$$f(x)=x^4-5x^3+3x^2-4x+1$$
$$\begin{eqnarray}f'(x)&=&(x^4)’-(5x^3)’+(3x^2)’-(4x)’+(1)’\\[5pt]&=&4x^3-15x^2+6x-4 \end{eqnarray}$$
【微分法のやり方】導関数の公式(数学Ⅲ)
ここからは理系の方のみ学習する範囲になります。
積の導関数
$$\{f(x)g(x)\}’=f'(x)g(x)+f(x)g'(x)$$
次の関数を微分しなさい。
$$f(x)=(x^2-2)(x^3+2x-1)$$
展開をしてから微分をしていってもいいのですが、式が長くなってしまいメンドイですね。
こういう場合には、積の導関数公式を使っていきましょう。
イメージとしては
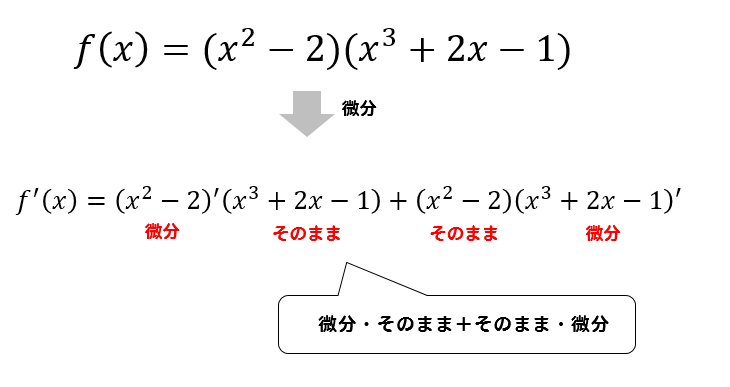
こんな感じです。
$$\begin{eqnarray}f'(x)&=&(x^2-2)(x^3+2x-1)\\[5pt]&=&(x^2-2)'(x^3+2x-1)+(x^2-2)(x^3+2x-1)’\\[5pt]&=&2x(x^3+2x-1)+(x^2-2)(3x^2+2)\\[5pt]&=&2x^4+4x^2-2x+3x^4+2x^2-6x^2-4 \\[5pt]&=&5x^4-2x-4\end{eqnarray}$$
商の導関数(分数の微分)
次の関数を微分しなさい。
$$f(x)=\frac{2x-1}{x^2+1}$$
分数の形になっている関数は、商の導関数公式を使って微分していきます。
イメージとしては

こんな感じだね。
$$\begin{eqnarray}f'(x)&=&\frac{(2x-1)'(x^2+1)-(2x-1)(x^2+1)’}{(x^2+1)^2}\\[5pt]&=&\frac{2(x^2+1)-2x(2x-1)}{(x^2+1)^2} \\[5pt]&=&\frac{-2x^2+2x+2}{(x^2+1)^2}\end{eqnarray}$$
合成関数の微分法
上の公式だけを見ると、なんのこっちゃ分かりにくい(^^;)
実際に例題を見ていきましょう。
次の関数を微分しなさい。
$$f(x)=(x^2-3)^3$$
合成関数の微分では、次のようなイメージで計算していきます。
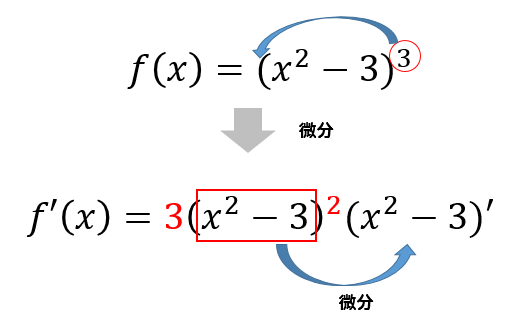
$$\begin{eqnarray}f'(x)&=&3(x^2-3)^2(x^2-3)’\\[5pt]&=&6x(x^2-3)^2 \end{eqnarray}$$
三角関数の導関数
$$(\cos x)’=-\sin x$$
$$(\tan x)’=\frac{1}{\cos^2 x}$$
次の関数を微分しなさい。
$$y=\sin 2x$$
$$y’=\cos 2x \cdot (2x)’$$
$$=2\cos 2x$$
次の関数を微分しなさい。
$$y=\cos (x^2+1)$$
$$y’=-\sin (x^2+1) \cdot (x^2+1)’$$
$$=-2x\sin (x^2+1)$$
次の関数を微分しなさい。
$$y=\tan 3x$$
$$y’=\frac{1}{\cos^2 3x} \cdot (3x)’$$
$$=\frac{3}{\cos^2 3x}$$
それぞれこのように計算することができます。
他の三角関数についての難しい微分計算は
>【sin,cos,tanの微分】例題を解説!2乗、分数のときにはどうやる?
こちらの記事でまとめているのでご参考ください。
指数、対数関数の導関数
$$(\log_a|x|)’=\frac{1}{x\log a}$$
$$(e^x)’=e^x$$
$$(a^x)’=a^x\log a$$
次の関数を微分しなさい。
$$y=\log3x$$
$$y’=\frac{(3x)’}{3x}=\frac{3}{3x}=\frac{1}{x}$$
次の関数を微分しなさい。
$$y=\log_a(x^2-1)$$
$$y’=\frac{(x^2-1)’}{(x^2-1)\log a}$$
$$=\frac{2x}{(x^2-1)\log a}$$
次の関数を微分しなさい。
$$y=e^{3x}$$
$$y’=e^{3x}(3x)’=3e^{3x}$$
次の関数を微分しなさい。
$$y=2^{-2x}$$
$$y’=(2^{-2x}\log 2)(-2x)’=(-2\log 2)\cdot 2^{-2x}$$
他の対数関数についての難しい微分計算は
こちらの記事でまとめているのでご参考ください。
【微分のやり方】まとめ!
お疲れ様でした!
数学Ⅱまでに学習する微分の計算は、とてもシンプルで簡単なものばかりでした。
一方、数学Ⅲに突入するとかなり難しくなる…(^^;)
なので、ここは問題集などを使って計算方法をしっかりと頭に叩き込んでおく必要がありますね。
基本的には、上で紹介してきたような公式を使えば問題を解くことはできるので、あとは練習あるのみだ。
ファイト(/・ω・)/
















コメントを残す