この記事では、高校数学の三角比で学習する
余弦定理
についてまとめていきます。
余弦定理とはどんなものか。
余弦定理の証明は?
余弦定理の覚え方や使い方は?
などについてお話を進めていきます。
この記事を通して、余弦定理の知識を深め、問題がすらすら解けるようになっちゃおう!
余弦定理の基本問題については、こちらの動画で解説しています(‘◇’)ゞ
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
余弦定理の公式
余弦定理
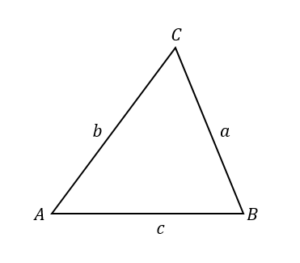
【辺の大きさを求める】
$$a^2=b^2+c^2-2bc\cos A$$
$$b^2=c^2+a^2-2ca\cos B$$
$$c^2=a^2+b^2-2ab\cos C$$
【角の大きさを求める】
$$\cos A=\frac{b^2+c^2-a^2}{2bc}$$
$$\cos B=\frac{c^2+a^2-b^2}{2ca}$$
$$\cos C=\frac{a^2+b^2-c^2}{2ab}$$
角の大きさを求めるときに使う、\(\cos A=\cdots\) の公式は次のように作ることができます。
$$\begin{eqnarray}a^2&=&b^2+c^2-2bc\cos A \\[5pt]2bc\cos A&=&b^2+c^2-a^2\\[5pt]\cos A&=&\frac{b^2+c^2-a^2}{2bc}\end{eqnarray}$$
なので、忘れてしまった場合でも自分で式を変形して思い出しましょう。
余弦定理の公式の覚え方
余弦定理って、どこの辺、角を使って式を作ればいいのか…
この判断に困ることがありますよね。
そんなときに覚えておいてもらいたいのが矢印型です!
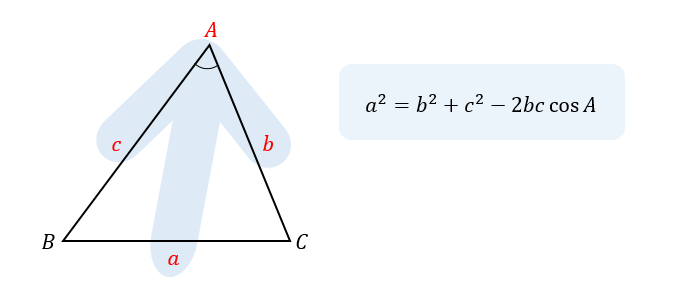
このように矢印の形になる部分の辺や角を使って式を作ればOKです。
余弦定理の公式証明
なぜ余弦定理の式が成り立つのか。
これは、直角三角形において三角比と三平方の定理を使うことで証明することができます。
次のような三角形を考える場合

$$a^2=b^2+c^2-2bc\cos A$$
が成立することを証明します。
まず、頂点Cから辺ABに垂線CHを下すと
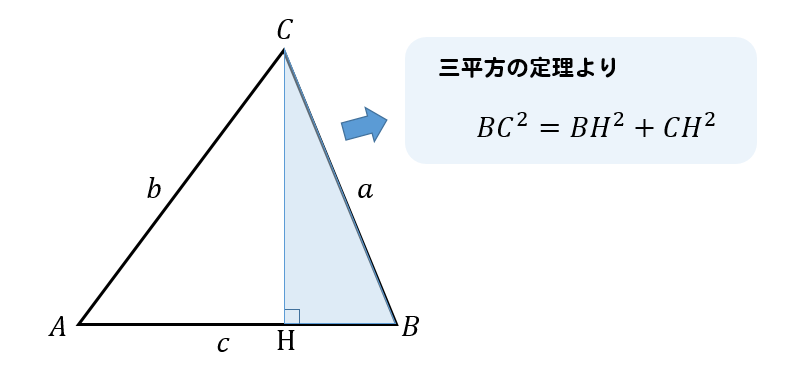
△BCHは直角三角形になるので、三平方の定理より
$$BC^2=BH^2+CH^2$$
という式がつくれます。
次に、角Aを基準に△ACHの直角三角形に注目すると
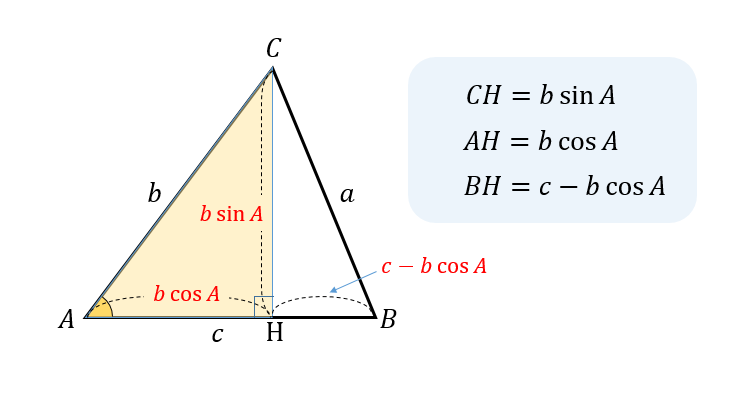
$$AH=b\cos A$$
$$CH=b\sin A$$
$$BH=AB-AH=c-b\cos A$$
と表すことができます。
すると、\(BC, BH, CH\) の大きさがそれぞれ表せたので
三平方の定理で作った\( BC^2=BH^2+CH^2\) の式に代入すると
$$\begin{eqnarray} a^2&=&(c-b\cos A)^2+(b\sin A)^2\\[5pt]a^2&=&c^2-2bc\cos A+b^2\cos^2 A+b^2\sin^2 A\\[5pt]a^2&=&c^2-2bc\cos A+b^2(\cos^2 A+\sin^2 A)\\[5pt]&\color{white}{=}&\sin^2 A+\cos^2 A=1だから\\[5pt]\color{red}{a^2}&\color{red}{=}&\color{red}{ c^2+b^2-2bc\cos A}\end{eqnarray}$$
このようにして、余弦定理の式を証明することができました。
鈍角三角形の場合の証明については
こちらの記事で詳しく解説しているのでご参考ください(^^)
余弦定理の問題計算
では、余弦定理を使う問題の計算について見ていきましょう。
辺の大きさを求める問題
△ABCにおいて、次のものを求めよ。
$$a=4, b=\sqrt{2}, C=45° のとき、c$$
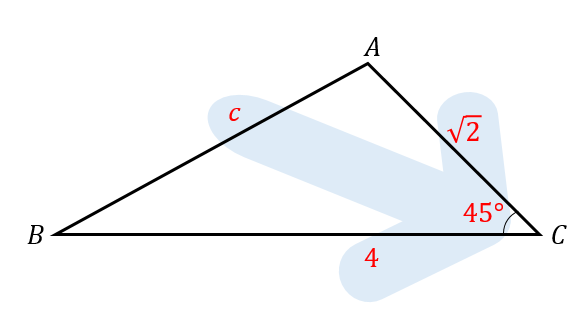
余弦定理は、上の図のように矢印の位置にある辺や角の大きさを使います。
$$\begin{eqnarray}c^2&=&4^2+(\sqrt{2})^2-2\cdot 4\cdot \sqrt{2}\cos 45°\\[5pt]c^2&=&16+2-8\sqrt{2}\cdot \frac{1}{\sqrt{2}}\\[5pt]c^2&=&10\\[5pt]c>0&\color{white}{=}&だから\\[5pt]c&=&\sqrt{10} \end{eqnarray}$$
答え
$$c=\sqrt{10}$$
△ABCにおいて、次のものを求めよ。
$$a=2, b=\sqrt{6}, B=60° のとき、c$$
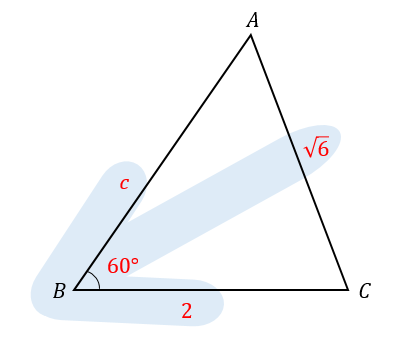
余弦定理は、上の図のように矢印の位置にある辺や角の大きさを使います。
$$\begin{eqnarray}\sqrt{6}^2&=&c^2+2^2-2\cdot c\cdot 2\cos 60°\\[5pt]6&=&c^2+4-4c\cdot \frac{1}{2}\\[5pt]0&=&c^2-2c-2\\[5pt]c&=&\frac{2\pm \sqrt{4+8}}{2}\\[5pt]&=&\frac{2\pm2\sqrt{3}}{2}\\[5pt]&=&1\pm\sqrt{3}\\[5pt]c>0&\color{white}{=}&だから\\[5pt]c&=&1+\sqrt{3} \end{eqnarray}$$
答え
$$c=1+\sqrt{3}$$
角度を求める問題
角度を求める問題では、次のように余弦定理を使います。
△ABCにおいて、次のものを求めよ。
$$a=3, b=5, c=7 のとき、C$$
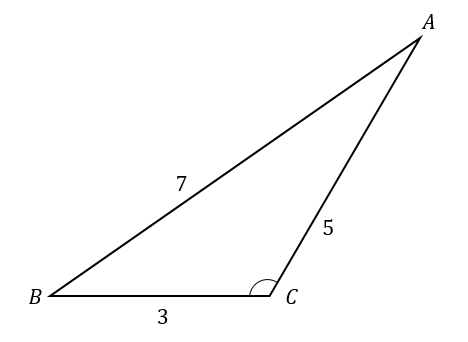
\(\cos C\)について求めたいので
\(\cos C=\frac{a^2+b^2-c^2}{2ab}\) の式にあてはめて計算していきます。
$$\begin{eqnarray} \cos C&=&\frac{3^2+5^2-7^2}{2\cdot 3\cdot 5}\\[5pt]&=&-\frac{1}{2}\end{eqnarray}$$
よって、\(C=120°\)
\(\cos C=\cdots\) という式を忘れてしまった場合には
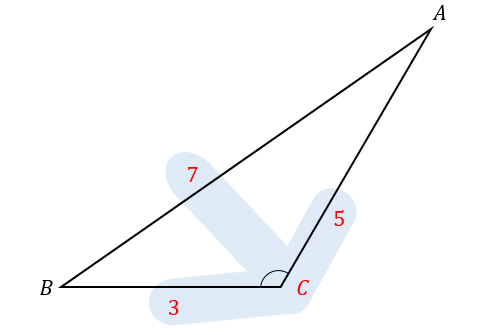
矢印型を使って、辺の長さを求めるときに使った公式にあてはめて計算していってもOKです。
$$\begin{eqnarray}7^2&=&3^2+5^2-2\cdot 3\cdot 5\cos C\\[5pt]49&=&9+25-30\cos C\\[5pt]30\cos C&=&34-49\\[5pt]\cos C&=&-\frac{15}{30}\\[5pt]\cos C&=&-\frac{1}{2} \end{eqnarray}$$
よって、\(C=120°\)
答え
$$C=120°$$
第1余弦定理、第2余弦定理とは
第1、第2余弦定理?
あまり聞き覚えのない言葉だと思いますが、以下のような公式が存在します。
第1余弦定理

$$a=c\cos B+b\cos C$$
$$b=a\cos C+c\cos A$$
$$c=b\cos A+a\cos B$$
これの証明は簡単です。
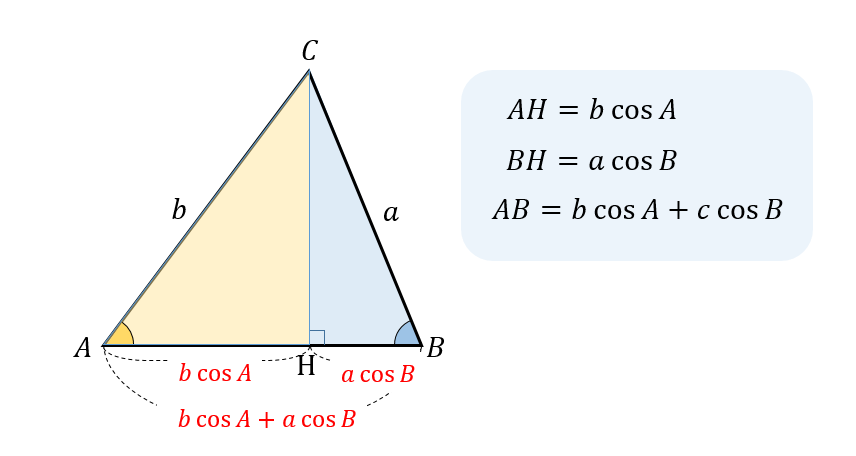
このように、三角形を2つの直角三角形に分けることで式を作ることができます。
この第1余弦定理というものを知っておくと、次のような問題で役に立ちます。
次の△ABCにおいて、\(a\)を求めよ。
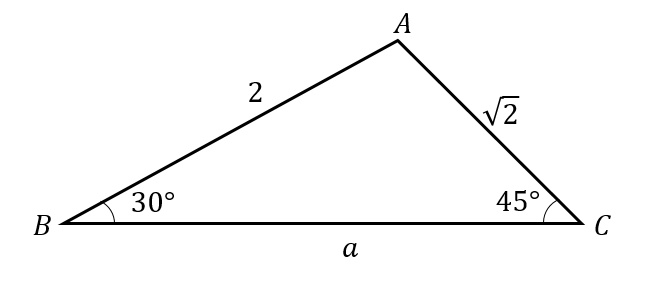
第1余弦定理より
$$\begin{eqnarray} a&=&c\cos B +b\cos C\\[5pt]&=&2\cos 30°+\sqrt{2}\cos 45°\\[5pt]&=&2\cdot \frac{\sqrt{3}}{2}+\sqrt{2}\cdot \frac{1}{\sqrt{2}}\\[5pt]&=&\sqrt{3}+1\end{eqnarray}$$
このように計算することができました。
通常の余弦定理を使うよりも、計算がシンプルで楽でしたね。
では、第2余弦定理とは?という話になりますが
これはみなさんご存知の通常バージョンの余弦定理
第2余弦定理

$$a^2=b^2+c^2-2bc\cos A$$
$$b^2=c^2+a^2-2ca\cos B$$
$$c^2=a^2+b^2-2ab\cos C$$
これを第2余弦定理といいます。
この章で紹介した第1、2余弦定理については知らなくても問題はありません。
ただ、知っておくと問題を解いていく上でちょっとだけラクができますよ!ってことで紹介しておきました。
余弦定理の公式まとめ!
お疲れ様でした!
余弦定理は、式を丸暗記するというよりも
図形から、辺や角の場所を見ながら式を作ることの方が多いでしょう。
そのため、矢印型の辺、角を使うというのが大事なポイントになりますね!
余弦定理って、なかなか覚えれないんですよ…
という方は、矢印型を意識すること!
そして、たくさん問題を解くこと!
数学の公式はにらめっこでは覚えれません。
とにかく手を動かして、体に覚えこませていきましょう!
余弦定理が理解できたら、次は正弦定理だ!
>【正弦定理】公式の証明は??問題の解き方をイチから解説するぞ!

















コメントを残す