こんにちは!数スタの小田です。
今回は高校数学Ⅱで学習する図形と方程式の単元から「直線に関して対称な点の座標」についてイチから解説していきます。
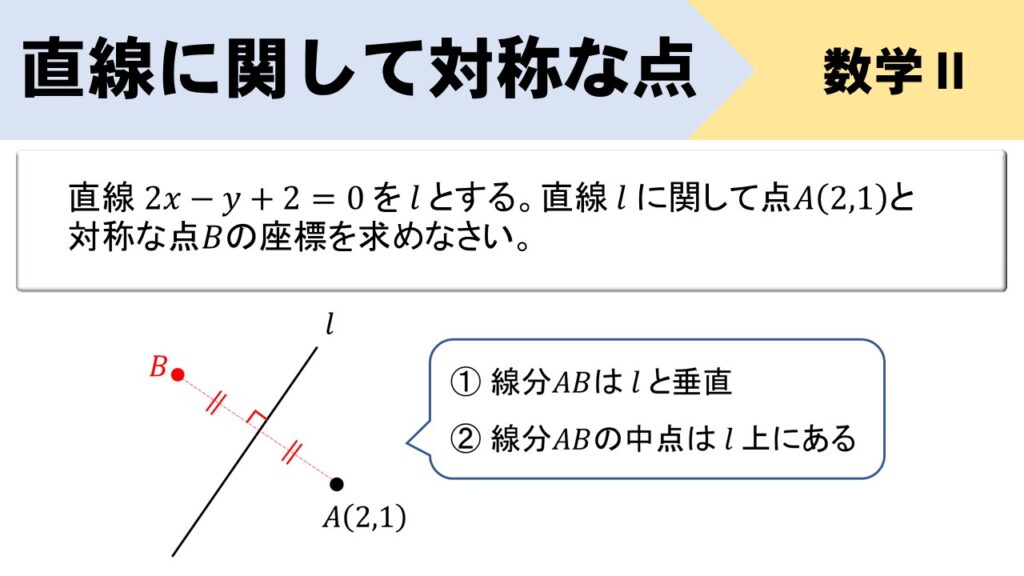
今回取り上げる問題はこちら!
【問題】
直線 \(2x-y+2=0\) を \(l\) とする。直線 \(l\) に関して点\(A(2,1)\) と対称な点\(B\)の座標を求めなさい。
ここでは「2STEPのポイントをおさえること」「式変形をおさえておくこと」。
この2点をおさえておけば簡単に求めることができるようになりますよ(‘ω’)ノ
今回の内容をサクッと理解したい方はこちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
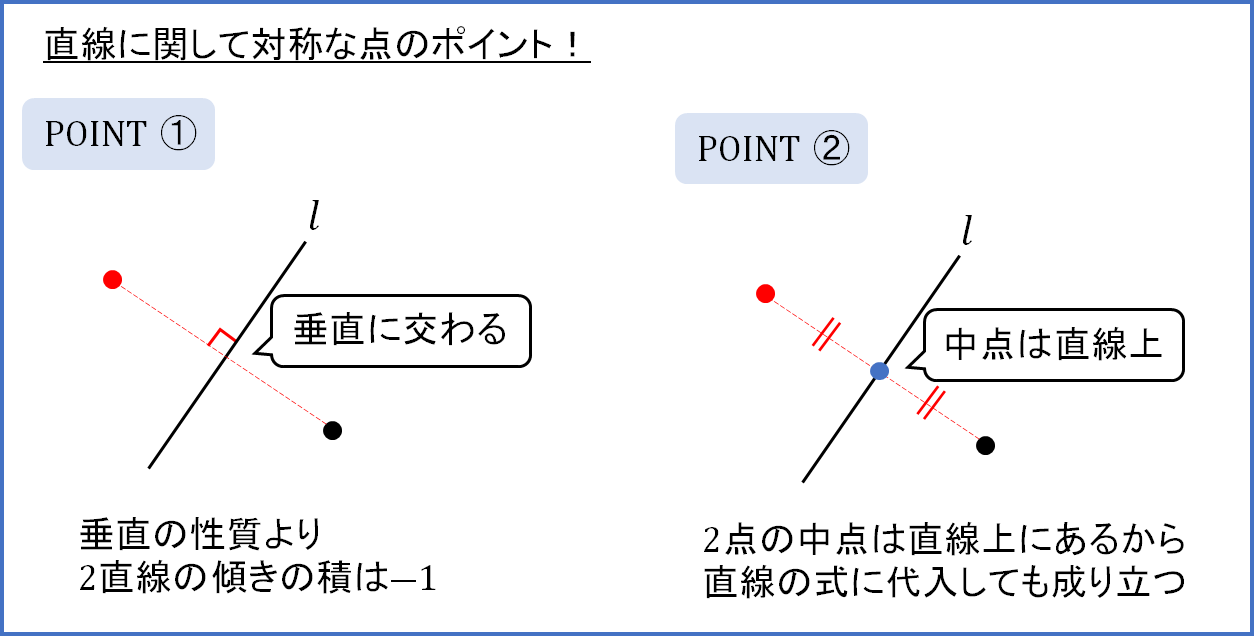
覚えておきたい2STEP!
直線に関して対称な点というのは次のようなイメージです。
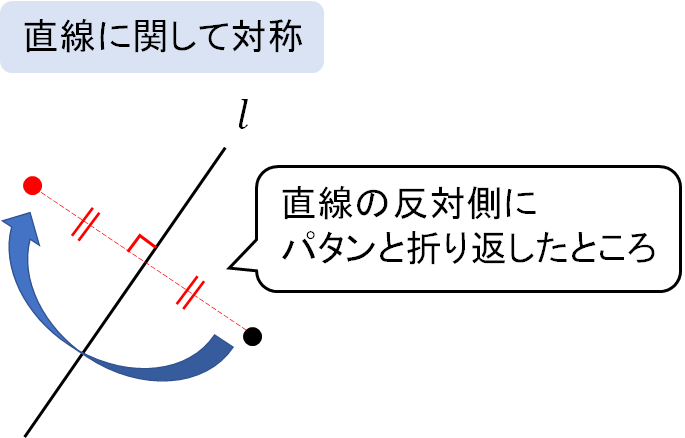
ここでポイントとなるのが次の2つ!
この2つのポイントを活用しながら座標を求めていくことになるのですが、その流れについて確認していきましょう。
2STEPで問題を解いてみよう!
【問題】
直線 \(2x-y+2=0\) を \(l\) とする。直線 \(l\) に関して点\(A(2,1)\) と対称な点\(B\)の座標を求めなさい。
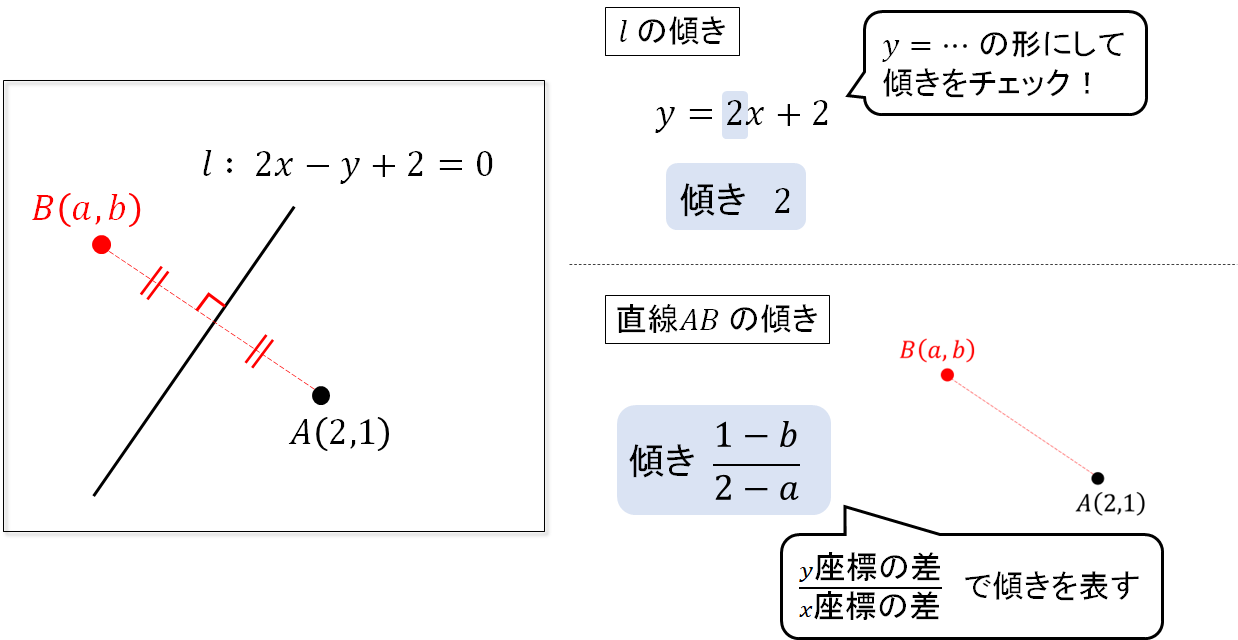
まずは、求めたい点\(B\)の座標を\((a,b)\)として求めていきましょう。
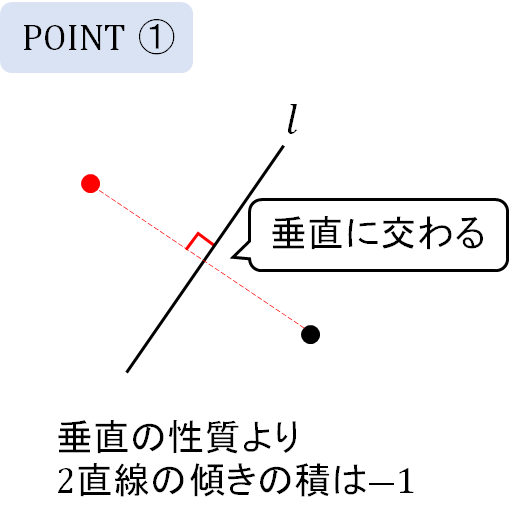
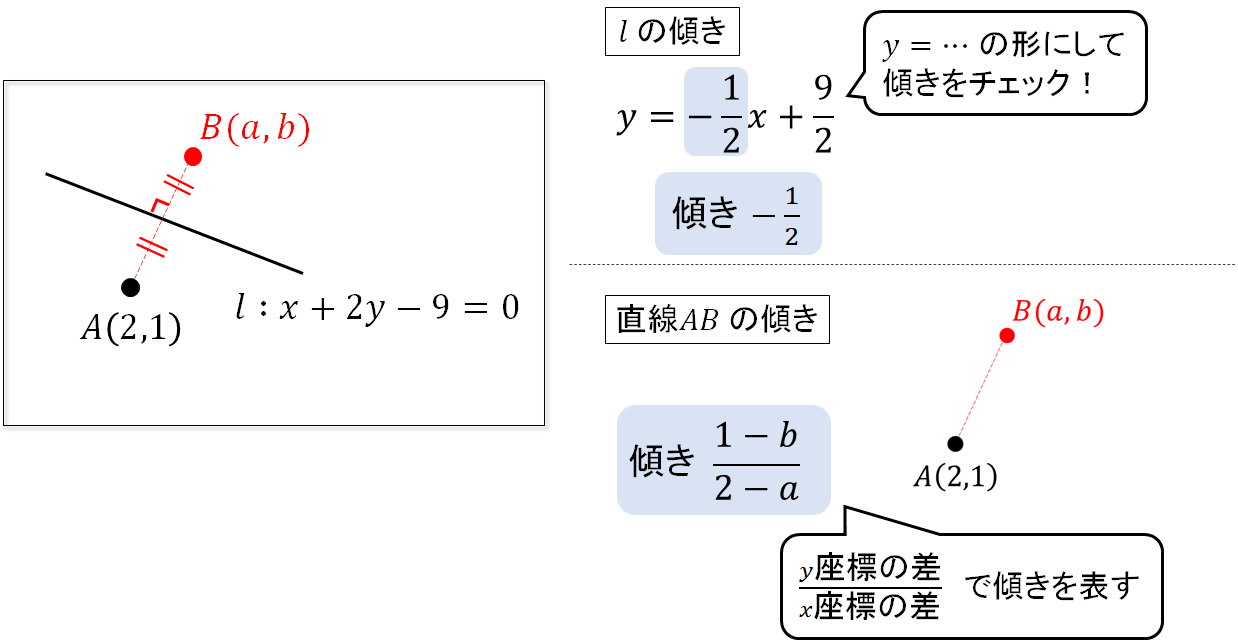
STEP1 傾きが垂直
直線\(l\) と2点を結ぶ直線は垂直に交わります。
なので、それぞれの傾きをかけると\(-1\)になりますね。

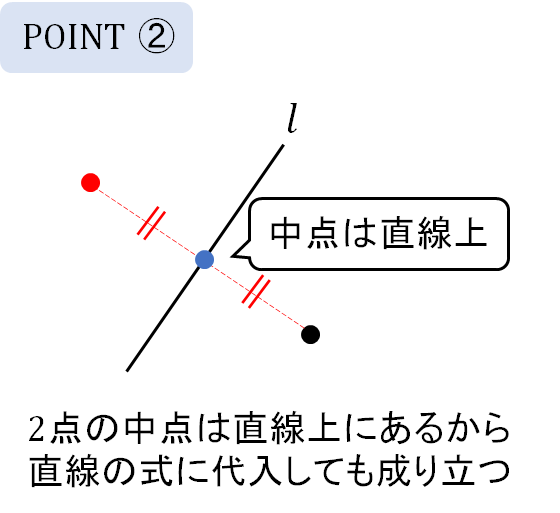
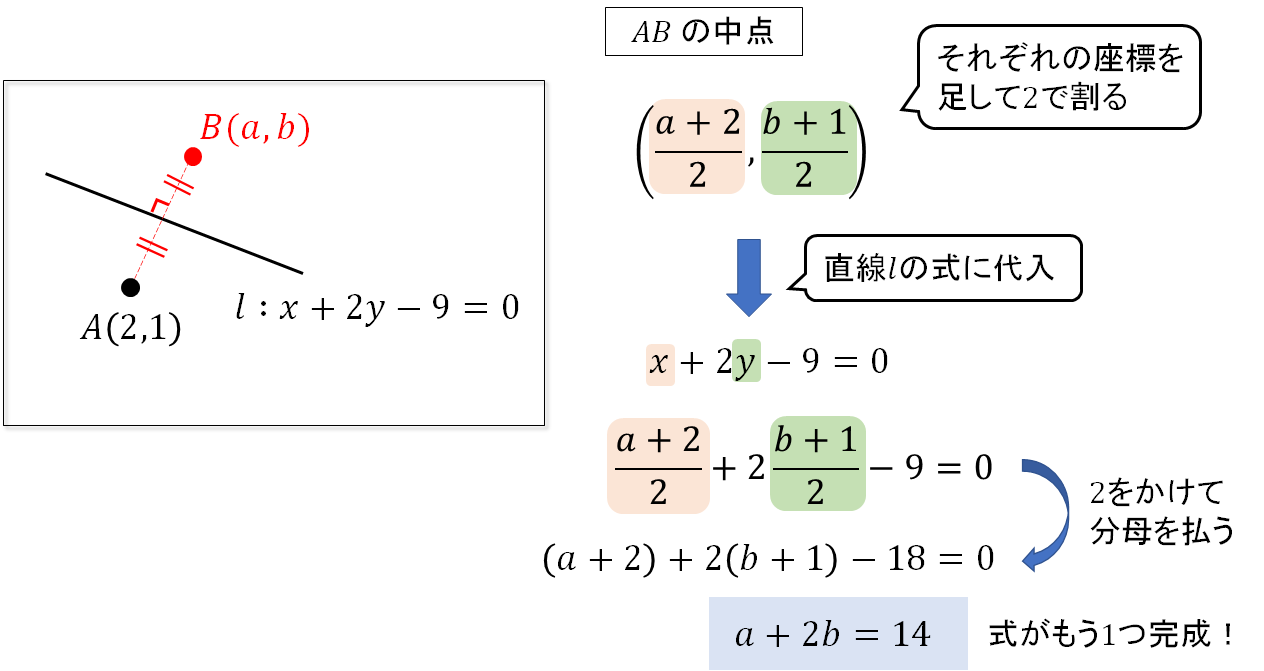
STEP2 中点は直線上
次は2点の中点を求めて、直線の式に代入しましょう!
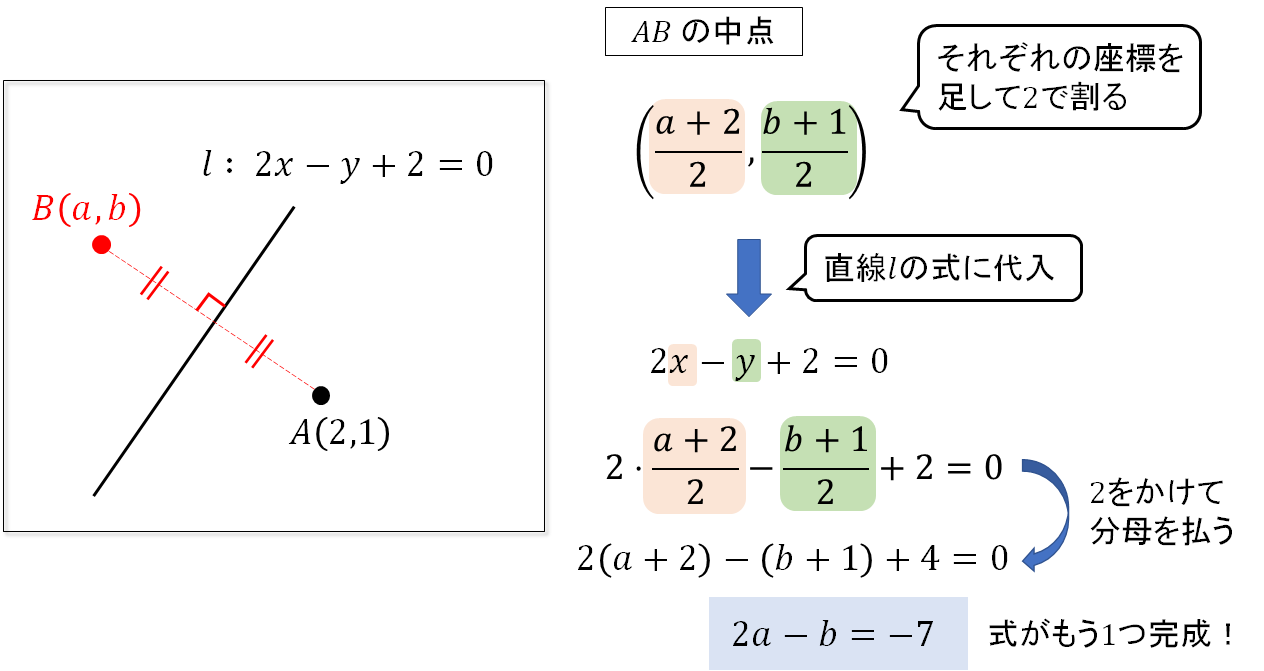
これで2つの式がつくれたので、あとは連立方程式で計算していけばOK!
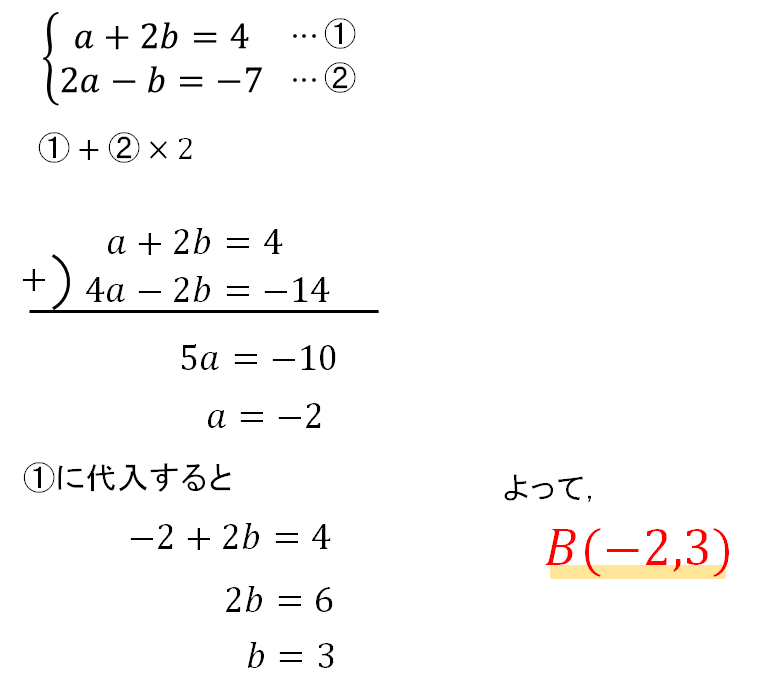
2STEPの流れは理解していただけましたか??
ここはテストに出題されやすい問題なので、演習問題を通してしっかりと理解をしておきましょう!
演習問題で理解を深めよう!
【問題】
直線 \(x+2y-9=0\) を \(l\) とする。直線 \(l\) に関して点\(A(2,1)\) と対称な点\(B\)の座標を求めなさい。
まとめ
では、最後にポイントをまとめておきましょう!
ここは途中の計算で分数がでてくるので、式変形でつまずく人が多い!
分数は分母を払ってシンプルな式に変換することを心掛けてくださいね^^



















コメントを残す