こんにちは!数スタの小田です。
今回は高校数学Ⅱで学習する式と証明の単元から「等式の証明」についてイチから解説していきます。
取り上げる問題はこちら!
【問題①】次の等式が成り立つことを証明しなさい。
(1) \(a^3-b^3=(a-b)^3+3ab(a-b)\)
(2) \((1+x)^3=1+x+x(1+x)+x(1+x)^2\)
【問題②】\(a+b+c=0\) のとき、次の等式を証明しなさい。
$$a^2+ca=b^2+bc$$
【問題③】 \(\frac{a}{b}=\frac{c}{d}\) のとき、次の等式を証明しなさい。
$$\frac{a+c}{b+d}=\frac{ad+bc}{2bd}$$
今回の内容をサクッと理解したい方はこちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
等式を証明する3つのパターン
まずは等式を証明する方法を確認しておきましょう。

この3つの方法があるのですが、証明したい等式の形を見ながら①②のどちらかを使っていくことになります。
(③は使っても良いですが、あまり積極的に使うことはないかな…)
それでは問題を見ながら証明のやり方を確認していきましょう!
【問題①】(1)の証明
【問題①】次の等式が成り立つことを証明しなさい。
(1) \(a^3-b^3=(a-b)^3+3ab(a-b)\)
まずは左辺、右辺の形をチェック!

すると、左辺の式は展開ができません。
展開できない式が含まれている場合には①パターンの証明方法をやっていきましょう!
展開できる方の式(右辺)を計算していき、左辺と同じになることを確かめます。

証明のかき方としては、点線で囲っている部分を答案に書いてもらえばOKです!
【問題①】(2)の証明
【問題①】次の等式が成り立つことを証明しなさい。
(2) \((1+x)^3=1+x+x(1+x)+x(1+x)^2\)
まずは左辺、右辺の形をチェック!

すると、今回は左辺、右辺ともに展開ができますね。
なので、②パターンの証明方法でやっていきましょう!
左辺を展開、右辺も展開、それぞれが同じ形になることを確かめます。

証明のかき方としては、点線で囲っている部分を答案に書いてもらえばOKです!
【問題②】条件付きの証明
【問題②】\(a+b+c=0\) のとき、次の等式を証明しなさい。
$$a^2+ca=b^2+bc$$
証明の方針として、条件式を等式に代入して文字を減らしていきましょう!

条件式を代入できるのが左辺だけなので①パターンの証明方法でやっていきましょう。
左辺に\(a=-b-c\)を代入して右辺と同じ形になることを確かめます。

証明のかき方としては、点線で囲っている部分を答案に書いてもらえばOKです!
条件式は\(a=\cdots\)に変形しましたが、\(b=\cdots, c=\cdots \)にしてもOKです!
【問題③】分数(比例式)の証明
【問題③】 \(\frac{a}{b}=\frac{c}{d}\) のとき、次の等式を証明しなさい。
$$\frac{a+c}{b+d}=\frac{ad+bc}{2bd}$$
条件式が分数(比例式)になっているときには、次のように「\(=k\)」とおいて代入するパーツをつくりましょう。
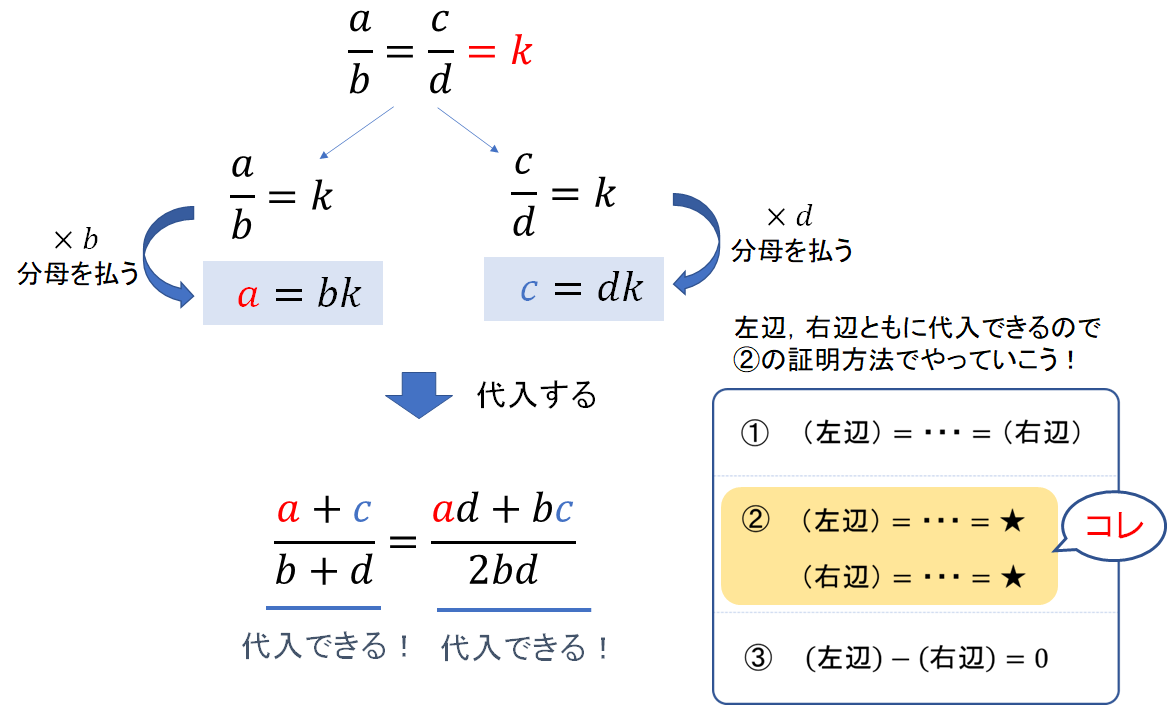
分数の条件式から \(a=bk, c=dk\) という2つの式がつくれたので、これを等式の左辺、右辺に代入して同じ形になることを確かめていきます。

証明のかき方としては、点線で囲っている部分を答案に書いてもらえばOKです!
条件式が分数の形だったら「\(=k\)」とおくことを覚えておきましょう(‘ω’)ノ
まとめ
お疲れ様でした^^
最後に証明3パターンの型を確認しておきましょう。

基本的には①②を使いまわしていくようになります。
展開、代入できる式が一方にしかない場合には①のパターン。
左辺、右辺ともに展開、代入できる場合には②のパターン。
このように覚えておくとイイですね^^
証明とは言え、やっていることはただの計算なのであまり難しく考えずに解いていってください!
では、今回は以上です(‘ω’)ノ















コメントを残す