\(180-\theta\),\(90-\theta\),\(90+\theta\)
うぉーーー!!
どうやって変形するのか忘れた!
ってか、何度やっても覚えられねぇ…
という方に向けて、これらの変形の覚え方、使い方についてまとめていきますね!



数式がスマホ画面からはみ出している場合には、横にスライドしてみてください。
もしくは、スマホの画面を横にしていただくとすべて表示されます。
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
\(180-\theta\),\(90-\theta\),\(90+\theta\)の覚え方
これらの変形は、単位円と合わせて覚えておくと便利です。
単位円上の \(x\)座標が \(\cos\)、\(y\)座標が \(\sin\)、傾きが \(\tan\) でしたね。
これを用いて、\(\theta\) とそれ以外の角との関係性を見ていけば簡単に理解することができます。
また、数学Ⅱで学習する加法定理を用いると、公式を自分で導くことができるようになります。
加法定理での導き方も合わせて紹介していきますね!
\(90-\theta\) の覚え方と使い方
\((90°-\theta)\)と \(\theta\) は次のような位置関係になります。
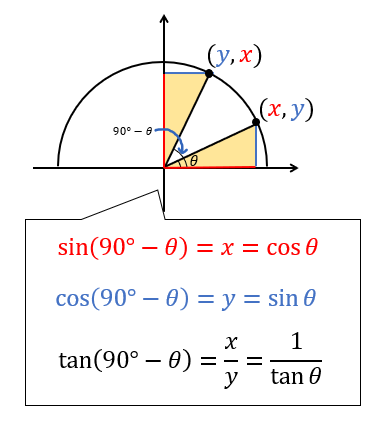
\((90°-\theta)\) の \(y\) 座標は、 \(\theta\) の \(x\) 座標と、
\((90°-\theta)\) の \(x\) 座標は、 \(\theta\) の \(y\) 座標と一致してることが分かります。
\((90°-\theta)\) と \(\theta\) は、ともに第1象限にあるので符号の変化はありませんね。
$$\sin62°=\sin(90°-28°)=\cos28°$$
$$\cos53°=\cos(90°-37°)=\sin37°$$
$$\tan85°=\tan(90°-5°)=\frac{1}{\tan5°}$$
$$\begin{eqnarray}\sin(90°-\theta)&=&\sin90°\cos\theta-\cos90°\sin\theta\\[5pt]&=&\cos\theta \end{eqnarray}$$
$$\begin{eqnarray}\cos(90°-\theta)&=&\cos90°\cos\theta+\sin90°\sin\theta\\[5pt]&=&\sin\theta \end{eqnarray}$$
$$\begin{eqnarray}\tan(90°-\theta)&=&\frac{\sin(90°-\theta)}{\cos(90°-\theta)}\\[5pt]&=&\frac{\cos\theta}{\sin\theta}\\[5pt]&=&\frac{1}{\tan\theta} \end{eqnarray}$$
※\(\tan\) は三角比の相互関係を使っています。
\(90+\theta\) の覚え方と使い方
\((90°+\theta)\)と \(\theta\) は次のような位置関係になります。
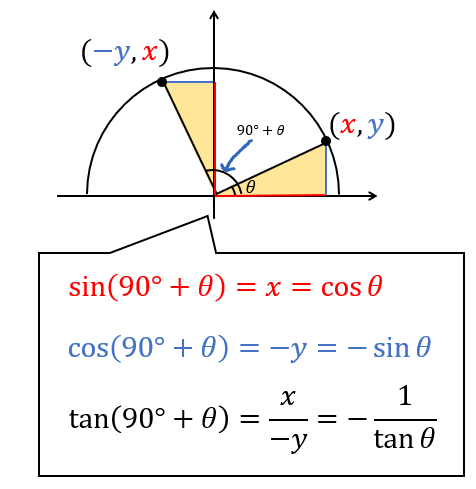
90°だけ回転移動した形になりますね。
\((90°+\theta)\) の \(y\) 座標は、 \(\theta\) の \(x\) 座標と、
\((90°+\theta)\) の \(x\) 座標は、 \(\theta\) の \(y\) 座標の符号をマイナスにしたものと一致してることが分かります。
$$\sin112°=\sin(90°+22°)=\cos22°$$
$$\cos98°=\cos(90°+8°)=-\sin8°$$
$$\tan108°=\tan(90°+18°)=-\frac{1}{\tan18°}$$
$$\begin{eqnarray}\tan(90°-\theta)&=&\frac{\sin(90°+\theta)}{\cos(90°+\theta)}\\[5pt]&=&\frac{\cos\theta}{-\sin\theta}\\[5pt]&=&-\frac{1}{\tan\theta} \end{eqnarray}$$
※\(\tan\) は三角比の相互関係を使っています。
\(180-\theta\) の覚え方と使い方
最後に、\((180-\theta)\)と \(\theta\) の位置関係を確認しておきましょう。
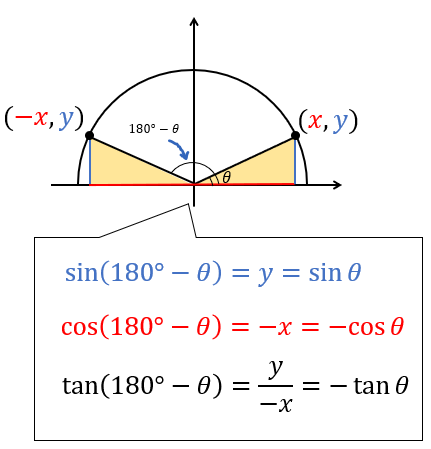
これが一番簡単!\(y\)軸について対称移動した形ですね。
\((180°-\theta)\) は\(\theta\) に比べて、
\(y\) 座標は変わらず、\(x\) 座標は符号をマイナスにしたものになっています。
$$\sin135°=\sin(180°-45°)=\sin45°$$
$$\cos154°=\cos(180°-26°)=-\cos26°$$
$$\tan146°=\tan(180°-34°)=-\tan34°$$
$$\begin{eqnarray}\tan(180°-\theta)&=&\frac{\sin(180°-\theta)}{\cos(180°-\theta)}\\[5pt]&=&\frac{\sin\theta}{-\cos\theta}\\[5pt]&=&-\tan\theta \end{eqnarray}$$
※\(\tan\) は三角比の相互関係を使っています。
\(180-\theta\),\(90-\theta\),\(90+\theta\)の問題に挑戦!
では、この章では三角比の角の変形を使った問題を紹介していきます。
どのように変形して答えを出していけばいいのか確認しておきましょう。
次の式の値を求めよ。
$$\sin^225°+\sin^265°$$
$$\begin{eqnarray}&&\sin^225°+\sin^265°\\[5pt]&=&\sin^225°+\sin^2(90°-25°)\\[5pt]&=&\sin^225°+\cos^225°\\[5pt]&=&1\cdots(解) \end{eqnarray}$$
2乗が出てきても同じように考えれば良いですね!
\(\sin^265°=(\sin65°)^2=(\cos25°)^2=\cos^225°\)
また、三角比の相互関係についても一緒に問われることが多いので、しっかりと覚えておきましょう。
- \(\sin^2\theta+\cos^2\theta=1\)
- \(\displaystyle{\tan\theta=\frac{\sin\theta}{\cos\theta}}\)
- \(\displaystyle{1+\tan^2\theta=\frac{1}{\cos^2\theta}}\)
次の式の値を求めよ。
$$\sin20°\cos70°+\cos20°\sin70°$$
なるべく小さい角に変形していくのがポイント!
20°はこれ以上小さく変形できないので、そのまま。
70°⇒20°に変形していくとコンパクトにまとまっていきます。
次の式の値を求めよ。
$$\sin110°+\cos160°+\tan10°+\tan170°$$
90°、180°どっちの変形を使えばいいんだろう?
と、疑問に思った方もいるかもしれませんね。
考え方はシンプル!
90°、180°のうち近い方を用いるようにしてください。
110°であれば、90°とは20°、180°とは70°の差があります。
すると、90°の方が近いってことが分かりますので、\((90°+\theta)\) の変形を用いるという判断になります。
次の式の値を求めよ。
これはかなり複雑な変形でしたね(^^;)
今回の\(\tan\) の変形では、最初に\((90°+\theta)\) の変形を使ってしまうと分数の形がでてきてしまって、計算がややこしくなります。
なので、最初は分数が出てこない\((180°-\theta)\) の変形を使い、式がコンパクトになってきたタイミングで \(90°\) を使った変形をしていくと良いです。
\(\sin\theta=\frac{1}{3}\) のとき,次の式の値を求めよ。
式を変形して、コンパクトになったところで代入していけばいいですね!
まとめ!
お疲れ様でした!
\(180-\theta\),\(90-\theta\),\(90+\theta\) の変形は覚えれましたか?
忘れてしまったときには、単位円をイメージしながら思い出すようにしてみてくださいね。
私も変形のやり方を忘れてしまうことがあるのですが、
その都度、単位円をイメージして思い出すようにしています(^^)
















間違い指摘
180-θの画像の中にある
「tan(180-θ)=-x/y」は
「tan(180-θ)=y/-x」では?
ご指摘ありがとうございました!
訂正しておきましたm(__)m
夏休み明けにやるであろう三角比の予習をしているのですが、「(90+θ)と(180−θ)ってどっちも第二象限なのに何が違うんだ?」と悩んでいました。
このページで本質まで十分理解できました、わかりやすく解説して頂きありがとうございます!
ややこしい内容ですからね(^^;)
理解のお役に立てたようでよかったです!
がんばってくださいね(‘◇’)ゞ