今回は中3で学習する二次方程式の単元から「動点の利用問題」について解説していきます。
「何秒後ですか?」「何cm動いたときですか?」
このように速さが絡むとき、どうでないときのパターンがあるので、それぞれの問題を取り上げて解き方をイチから確認していきます(‘◇’)ゞ
今回取り上げる問題はこちら!
《正方形の動点》
下の図のような一辺10㎝の正方形ABCDの辺上を動く2点P,Qがある。点Pは頂点Aは出発して,毎秒2㎝の速さで点Dに向かって動いていく。点Qは頂点Bを出発して,毎秒1㎝の速さで点Aに向かって動いていく。2点P,Qが同時に出発するとき,3点A,P,Qを頂点とする△APQの面積が16㎠となるのは何秒後か求めなさい。ただし,点Pが点Dに到達するまでのこととする。
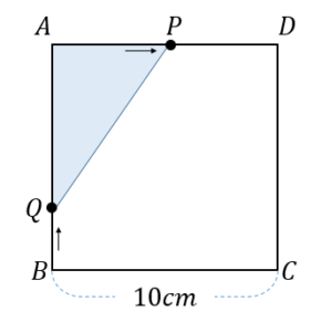
《直角三角形の動点》
下の図のような直角三角形がある。点Pは,Bを出発して辺AB上を,秒速2㎝の速さでAまで動く。点Qは,Cを出発して辺CB上を,秒速1㎝の速さで動き,点PがAにつくと同時に止まる。点P,QはそれぞれB,Cを同時に出発する。△PBQの面積が12㎠になるのは点Pが出発してから何秒後か求めなさい。
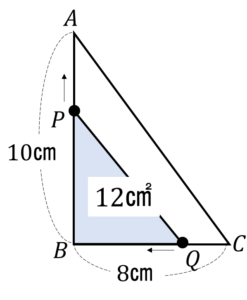
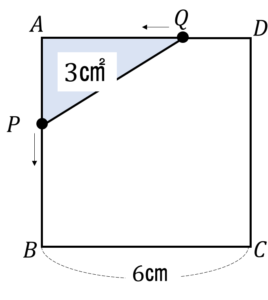
《動いた距離の動点》
下の図のような正方形ABCDで,点Pは,Aを出発して辺AB上をBまで動きます。また,点Qは,点PがAを出発するのと同時にDを出発し,Pと同じ速さで辺DA上をAまで動きます。点PがAを何㎝動いたとき,△APQの面積が3㎠になりますか。
今回の内容はこちらの動画でも解説しています!
細かいところは動画の方が伝わりやすいので、サクッと理解したい方はこちらをおススメします( `ー´)ノ

動点の利用~速さがある~
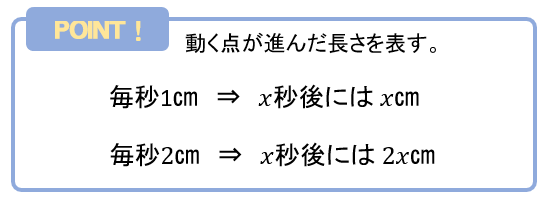
動点の問題で速さが与えられているときには、時間を \(x\)秒とおいて動いた距離を \(x\)を使って表しましょう。
正方形の動点
下の図のような一辺10㎝の正方形ABCDの辺上を動く2点P,Qがある。点Pは頂点Aは出発して,毎秒2㎝の速さで点Dに向かって動いていく。点Qは頂点Bを出発して,毎秒1㎝の速さで点Aに向かって動いていく。2点P,Qが同時に出発するとき,3点A,P,Qを頂点とする△APQの面積が16㎠となるのは何秒後か求めなさい。ただし,点Pが点Dに到達するまでのこととする。

まずは、時間を\(x\)秒後とおき、出発地点からそれぞれの場所までどれくらいの距離を動いたのか表しましょう。
すると、こんな感じですね!
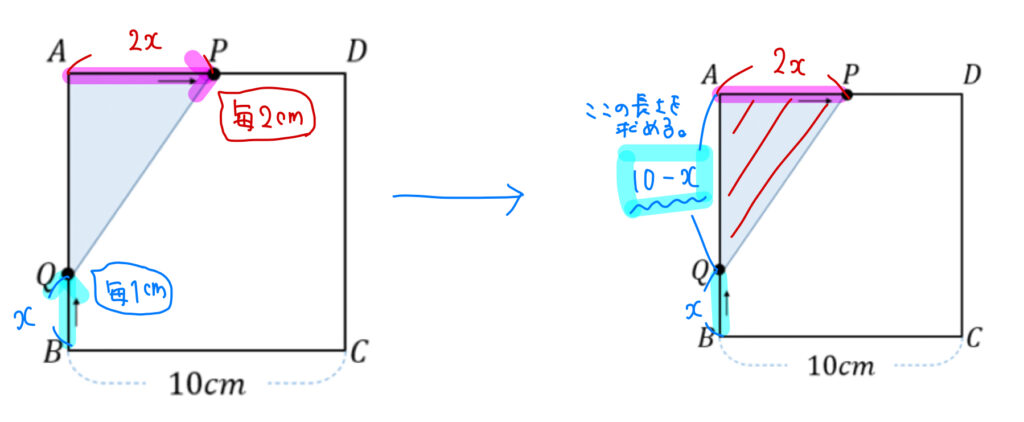
点Pは点Aから毎秒2㎝の速さで進んでいるのでAPの長さを\(2x\)。
同様に、点Qは点Bから毎秒1㎝の速さで進んでいるのでBQの長さを\(x\)と表せます。
ポイントは「出発地点からそれぞれの点がいるところまでの長さが表される」という点です。
あとは三角形に必要な辺の長さを表して、面積の式から方程式をつくりましょう。
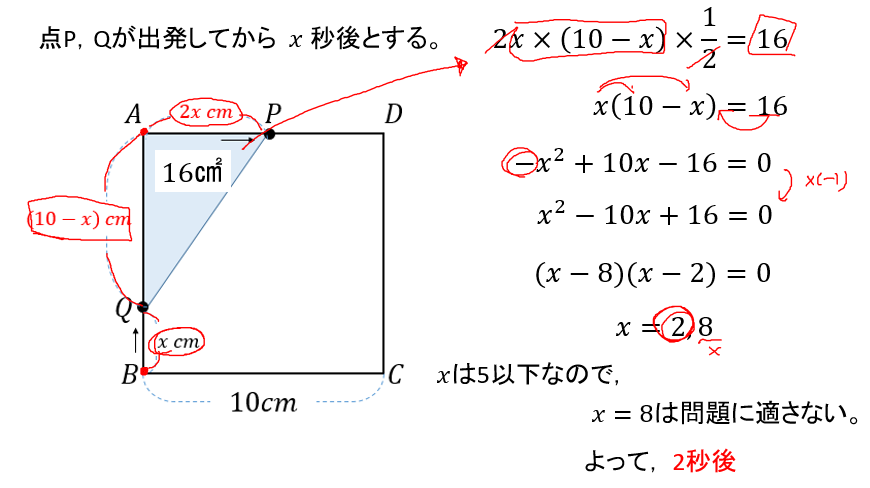
「点Pが点Dに到達するまで」とあることから、時間は5秒までであることが分かります。
よって、8秒は不適としてくださいね!
直角三角形の動点
下の図のような直角三角形がある。点Pは,Bを出発して辺AB上を,秒速2㎝の速さでAまで動く。点Qは,Cを出発して辺CB上を,秒速1㎝の速さで動き,点PがAにつくと同時に止まる。点P,QはそれぞれB,Cを同時に出発する。△PBQの面積が12㎠になるのは点Pが出発してから何秒後か求めなさい。

まずは、時間を\(x\)秒後とおき、出発地点からそれぞれの場所までどれくらいの距離を動いたのか表しましょう。
すると、今回はこんな感じですね!

△PBQの底辺、高さがそれぞれ表せたので、あとは方程式をつくって解いていきましょう!

「点Pが点Aにつくまで」とあることから、時間は5秒までであることが分かりますね。
なので、6秒は不適となります。
動点の利用~動いた長さ~
下の図のような正方形ABCDで,点Pは,Aを出発して辺AB上をBまで動きます。また,点Qは,点PがAを出発するのと同時にDを出発し,Pと同じ速さで辺DA上をAまで動きます。点PがAを何㎝動いたとき,△APQの面積が3㎠になりますか。

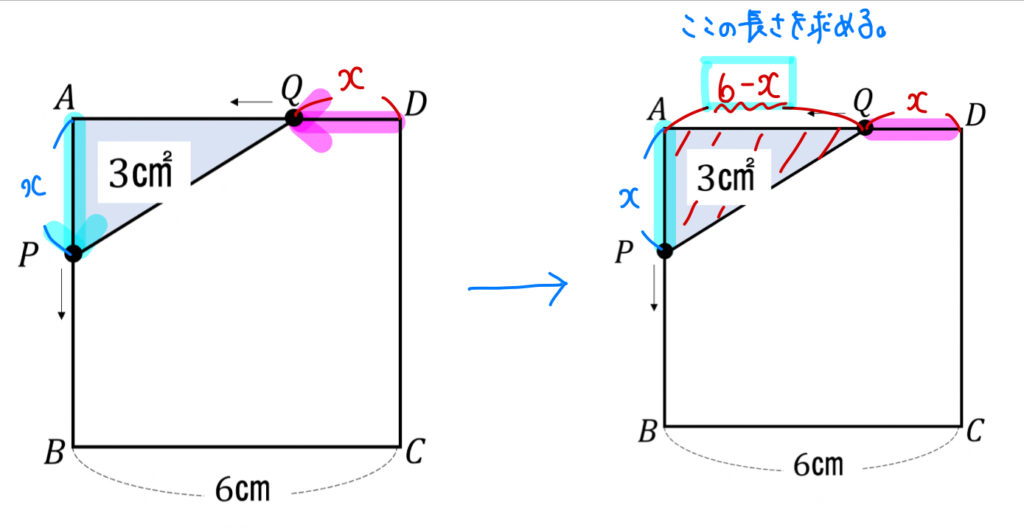
今回の問題では速さが具体的に与えられておらず「どれくらい動いたのか」だけが焦点になっています。
こういう場合にはシンプルに動いた距離をそれぞれ\(x\)cmとおいて考えていきましょう。
すると、こんな感じですね!
△APQの底辺、高さがそれぞれ表せたので、あとは方程式をつくって解いていきましょう!
ただし、今回の問題が難しいのはここからです。汗
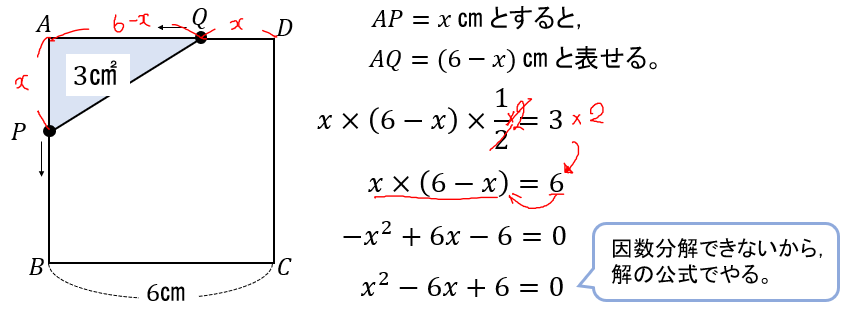

解の公式を使って、\(3+\sqrt{3}, 3-\sqrt{3} \) という2つの値が出てきます。
\(\sqrt{3}=1.73\cdots\) であることを考えると、ともに今回の問題に適していることが分かりますね。
ちょっと変な感じはあるかもしれませんが、ともに答えとしてください。
【追加演習】二次方程式の文章題をパターン別に攻略せよ!
今回は二次方程式の文章題特訓として、パターン別の演習課題を用意しました。
ここでは定期テストによく出題される「ある数、自然について」「図形」「箱の容積」「道幅」「動点」といった問題を取り上げています。これらが完璧に解けるようになれば、自信をもってテストに挑めるようになりますよ(‘ω’)ノ
動画解説も用意しているので、苦手な文章題も挫折することなく最後まで取り組めるはず!がんばってください^^
追加演習をやってテストの点数をUPさせたい方には、課題プリントをメールで送らせてもらっています。
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
まとめ
お疲れさまでした!
動点の問題は難しいと思われがちですが、動いた距離を文字で表すことができれば簡単に解けますよね^^
気をつけて欲しいのは、求まった値が問題に適しているかどうかをチェックすることです。
求まった値を使って、図形に当てはめてみながら適切な方を解に選ぶようにしてください!
















コメントを残す