今回の記事では
「外心、内心、重心の特徴とは」
についてサクッと解説しておきます。
外心とは、外接円の中心。
内心とは、内接円の中心。
重心とは、中線が交わる点。
では、それぞれどんな特徴があるのか確認しておきましょう。
外心の特徴、問題の解き方
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
外心とは、外接円の中心のことをいいます。
外接の円の中心、略して外心だね。
では、外心の特徴についてまとめておきましょう。
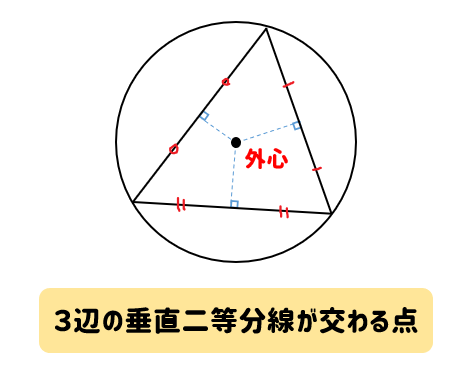
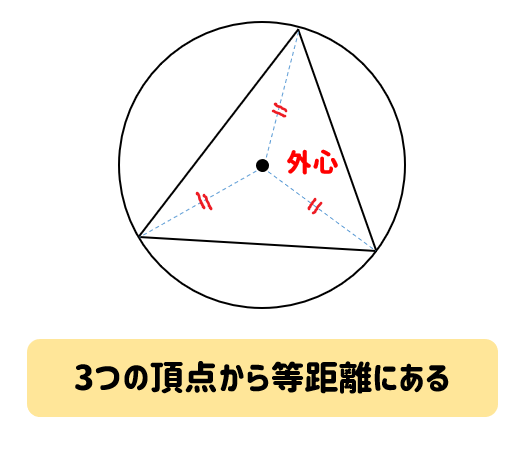
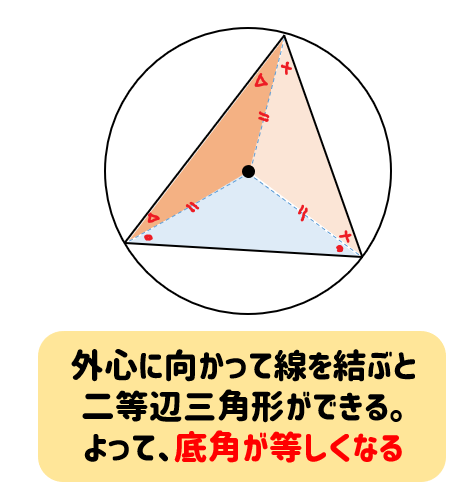
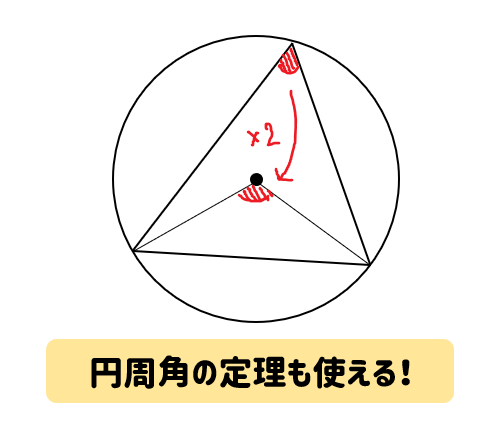
では、こられの特徴を使って問題を解いてみましょう。
【問題】
点Oは△ABCの外心である。このとき、\(x,y\)の大きさを求めなさい。
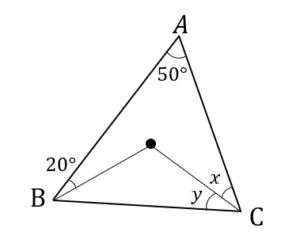
外心のときには、各頂点から外心に向かって補助線を引いてみましょう。
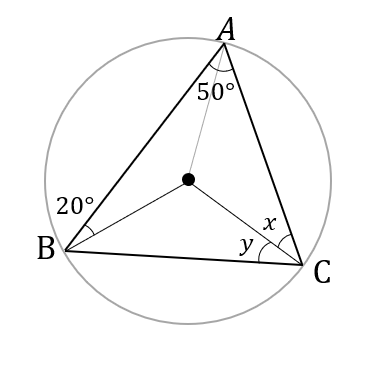
また、図に外接円を書き込んでおくと
どこの辺が等しくなるのかのイメージが湧きやすいです。
すると、二等辺三角形ができますね。
そこから角度をたどっていきます。
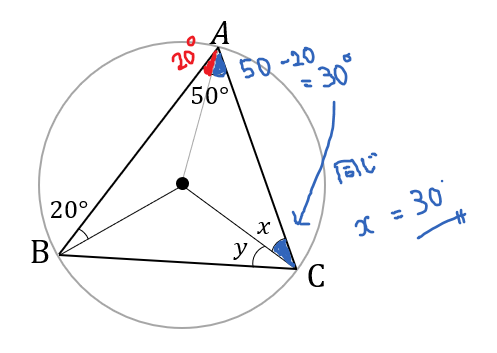
まずは二等辺三角形の底角をたどることで、\(x\)の大きさを求めることができました。
次は円周角の定理に着目して、\(y\)の大きさを求めてみましょう。
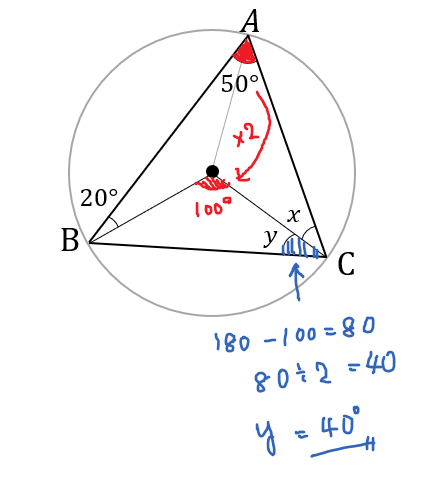
内心の特徴、問題の解き方
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
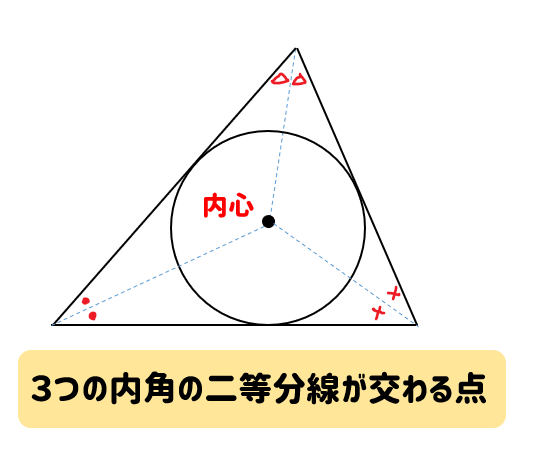
内心とは、内接円の中心のことをいいます。
内接の円の中心、略して内心だね。
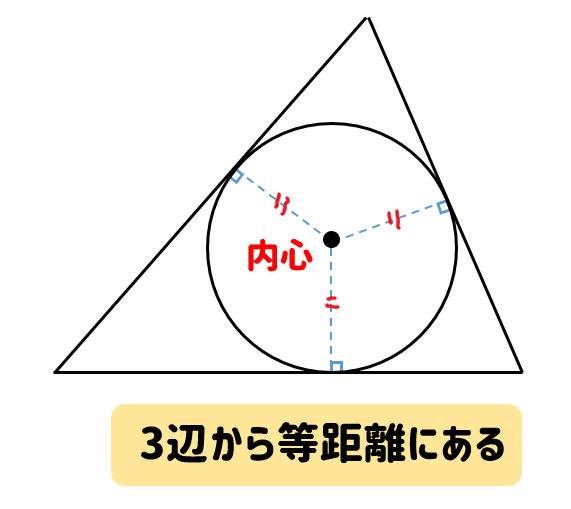
では、内心の特徴についてまとめておきましょう。
では、こられの特徴を使って問題を解いてみましょう。
【問題】
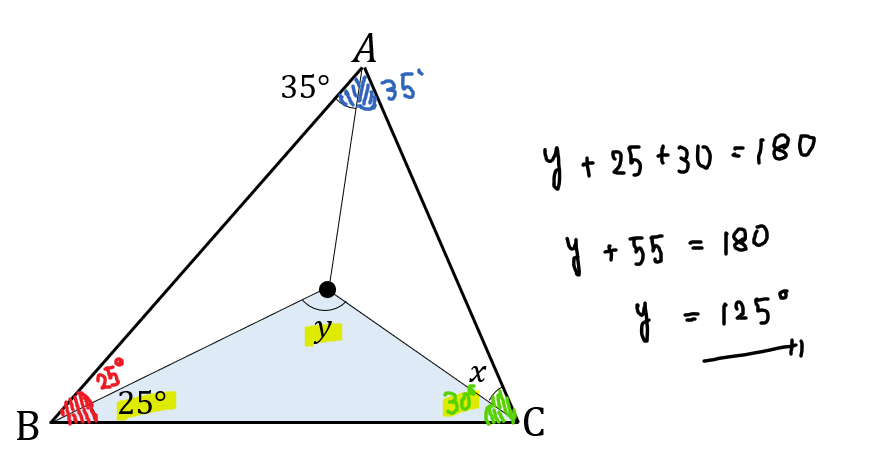
点Oは△ABCの内心である。このとき、\(x,y\)の大きさを求めなさい。
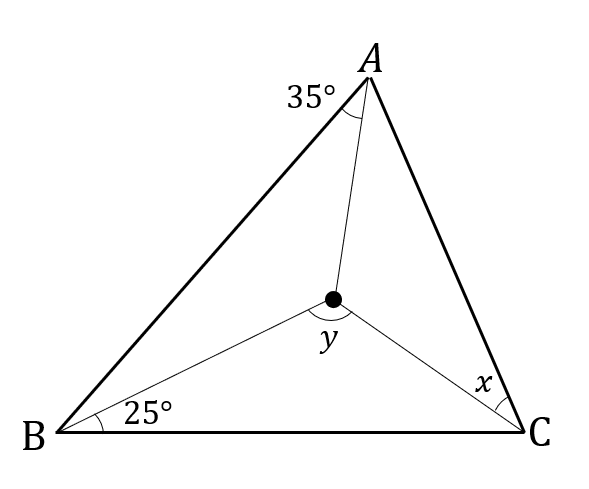
内心は角の二等分線がポイントです。
同じ角度になるところをたどりながら、\(x,y\)の大きさを求めましょう。
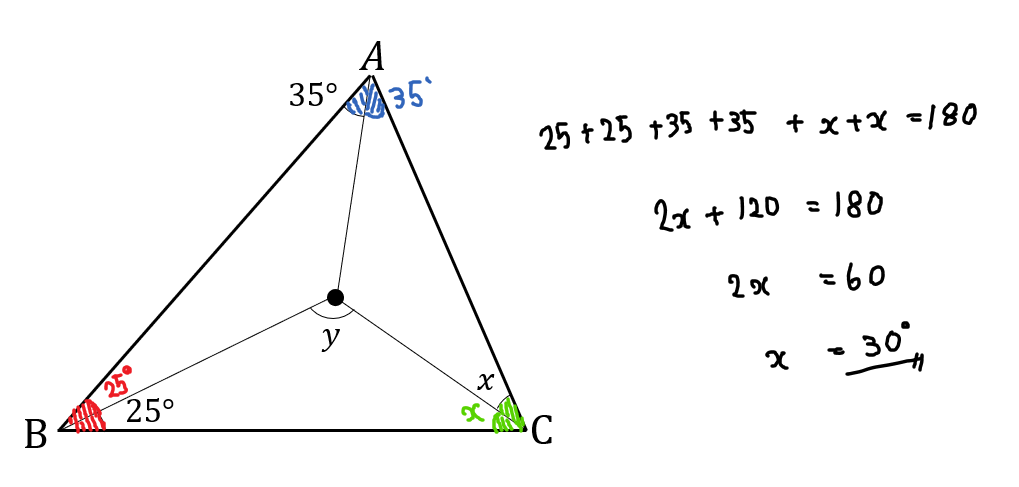
\(x\)の大きさが分かったら、\(y\)は簡単に求まりますね!
内心から線分の比を問われる問題もありますので、こちらの動画でやり方をチェックしておいてください!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
重心の特徴、問題の解き方
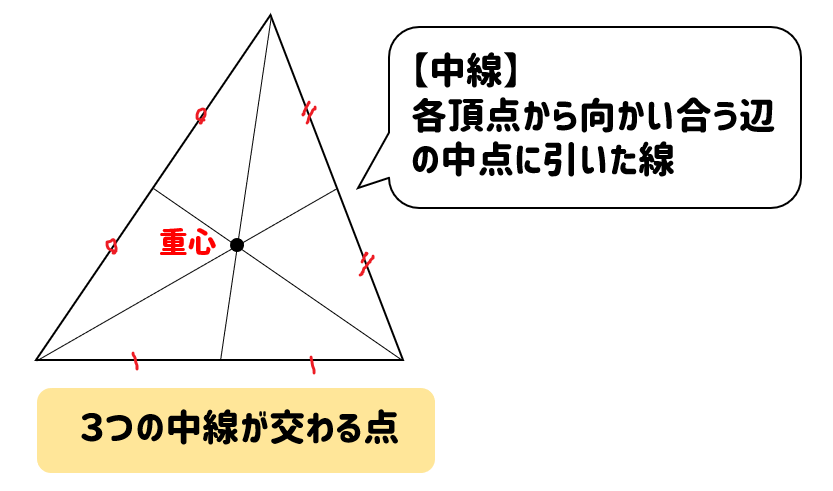
重心とは、3つの中線が交わる点のことをいいます。
※中線とは各頂点から向かい合う辺の中点に向かって引いた線のこと
では、重心の特徴についてまとめておきましょう。
では、こられの特徴を使って問題を解いてみましょう。
【問題】
△ABCの重心をGとする。このとき、△ABCと△ABGの面積比を求めなさい。
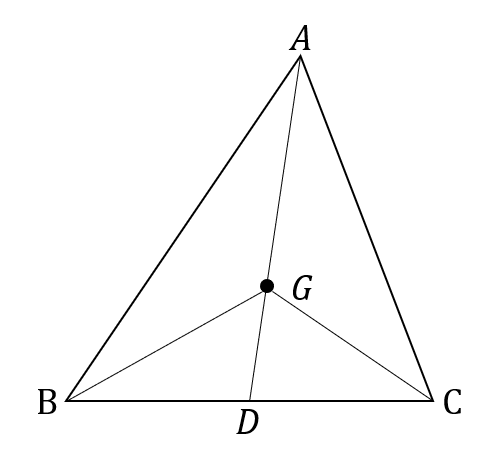
重心はその特徴から、面積比を考える問題が多いです。
どこが同じ長さか、どこが\(2:1\)になるのか。
この辺りがポイントとなります。
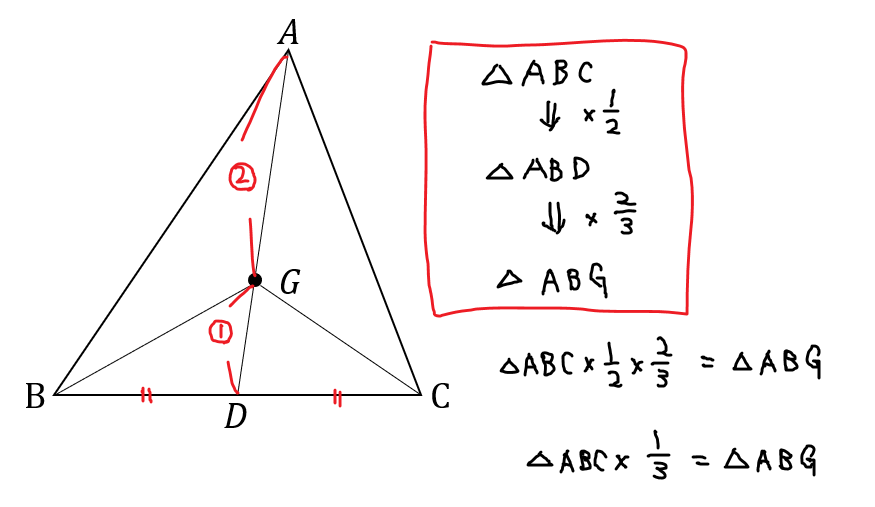
よって、△ABCと△ABGの面積比は\(3:1\)となります。
まとめ!
お疲れ様でした!
最後に外心、内心、重心のポイントをまとめておきましょう。
- 3辺の垂直二等分線が交わる点
- 各頂点から等しい距離にある
- 各頂点から線を結ぶと二等辺三角形ができるので、底角が等しい
- 円周角の定理が使える
【内心】
- 3つの角の二等分線が交わる点
- 3辺から等しい距離にある
【重心】
- 3つの中線が交わる点
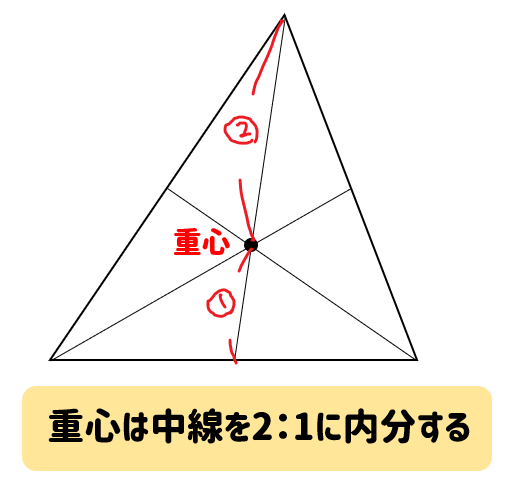
- 重心は中線を2:1に内分する















すっごい分かりやすくて助かります
よかったです^^
それぞれの特徴をおさえておくと
いろんな問題が解けるようになるから大事だね!
丁寧でわかりやすいです!YouTubeチャンネル登録させていただきました。
チャンネル登録めっちゃありがたいです!!
ありがとう‼︎
わかりやすい!
あざます
わかりやす!
とってもわかりやすい!!
大好き
さんくす
学校の授業よりわかりやすいです!
ありがとうございます!
う、嬉しいです!!
内心外心の基礎は克服出来ました!
へーーー^_^^_^^_^
このサイトが一冊にまとまった本が欲しいです。
紙の方が色々書き込めるし、覚えやすいから…
いつか本が出せたらいいなぁ
ここに内心の面積のことをたしてもらえたら、、、、最強です
ありがとうございます。数学過去最低点取っちゃって、立ち直れないかなって思ってたけど、やっぱり手を動かして証明してるのが一番楽しいです。
行動力が素晴らしい^^