【数学A】内分、外分の点はどこにある？場所の見つけ方をサクッと解説！

今回は高校数学Aで学習する

「内分、外分の点はどこ？」

というテーマについて解説していきます。

 

何となくは分かるけど

実際に点を書けと言われたら困るな…

という方も多いようなので、この記事ではイチから丁寧に解説していきますね(^^)

 

今回の内容はこちらの動画でも解説しています！

内分とは？点の書き方について

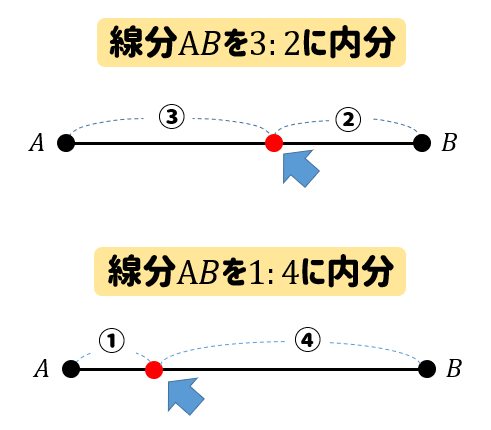
内分というのは簡単！

線分の内側を〇：△になるように分けたところを内分点といいます。

 

では、次のような問題ではどのように内分点を取ればよいのか確認してみましょう。

 

\(2:1\)に内分するということは

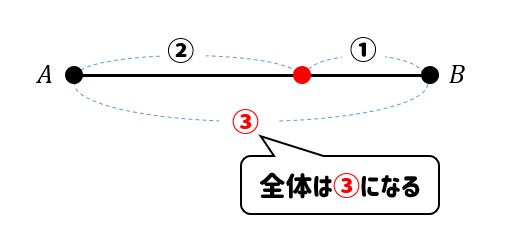
このように全体を\(3\)だと考えてることになるね。

 

ここから、\(2:1\)の比は何目盛り分を\(1\)と考えてるのかな？

というのを読み取りましょう。

すると、全部で6目盛りあって、それを\(3\)と考えているので

$$6\div 3=2$$

つまり2目盛りで\(1\)と考えてるってことになるね。

 

よって、線分ABを\(2:1\)に内分する点は次のようになります。

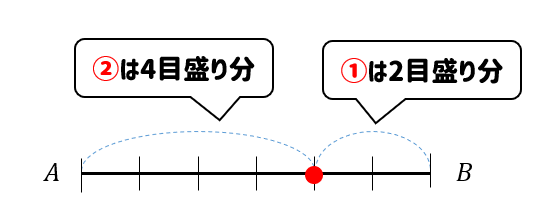
全体の目盛り、比から

1という比がどれくらいの目盛りを表しているのか考えるのがポイントですね！

外分とは？点の書き方について

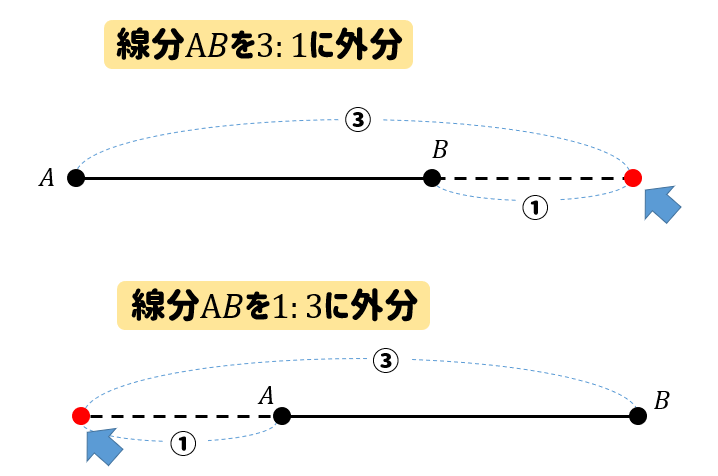
外分の方はすこしだけ注意が必要です！

 

最初の数が大きいときには

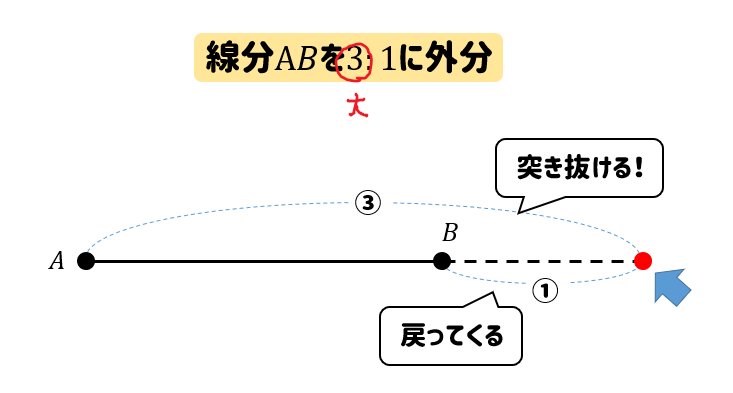
突き抜けてから、戻ってくる。

という点の取り方をします。

 

最初の数が小さいときには

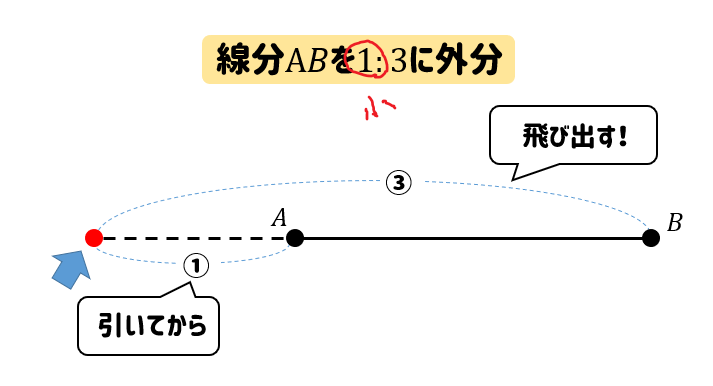
一度引いてから、飛び出す！

という点の取り方をします。

 

このように、外分点には2通りの取り方があるので注意しておきましょう。

また、内分点のときには全体の比がどうなるかを考えましたが

外分点の場合には「差」の比がどうなるかがポイントとなります。

 

では、次のような問題ではどのように外分点を取ればよいのか確認してみましょう。

 

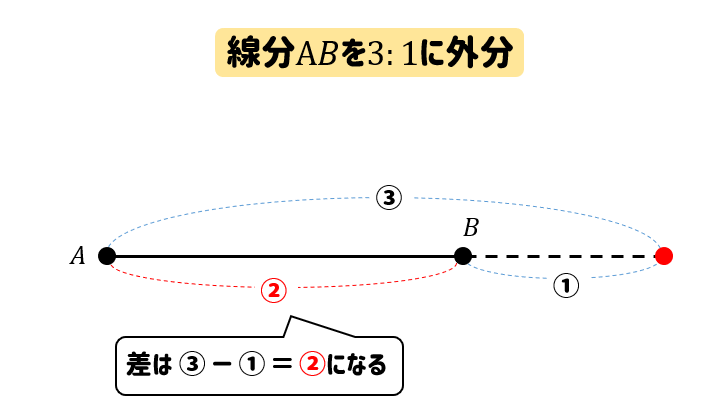
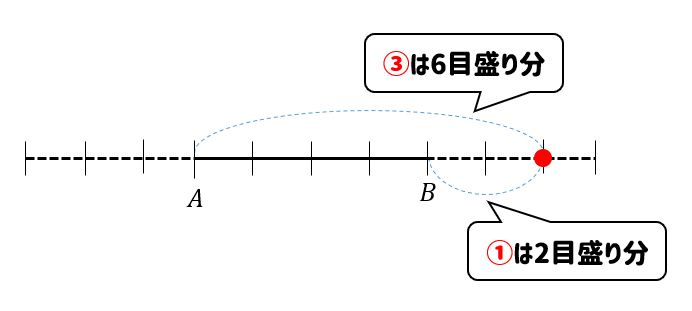
まずは、\(3:1\)に外分する点から考えてみましょう。

最初の数が大きいので、イメージとしてはこんな感じです。

すると、差であるAB部分は②の比になってることが分かりますね。

ってことは、4目盛りで②ということなので

$$4\div2=2$$

ということで、2目盛りで①となります。

 

よって、外分点は次のようになります。

 

 

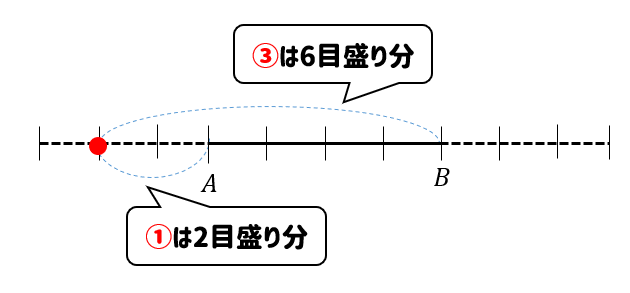
次に、\(1:3\)に外分する点を考えてみましょう。

最初の数が小さいので、一度引いてから飛び出すというパターンですね。

今回も差が②で4目盛りであることから、①で2目盛り分であることが読み取れます。

よって、外分点は次のようになります。

まとめ！

お疲れ様でした(/・ω・)/

内分点は全体の比を考える。

外分点は差の比を考える。

この2点が内分点、外分点を書くためには大事なポイントですね！

 

また、外分点については2パターンの書き方がありましたね。

ここが忘れがちだし、よく質問をいただくところです。

数が大なら突き抜けてから戻る。

数が小なら引いてから飛び出す。

この2パターンをしっかりと覚えておきましょう。