今回は高校数学Ⅱで学習する図形と方程式の単元から「内分点、外分点の座標の求め方」についてイチから解説していきます!
教科書に載ってる公式はこんな感じ…
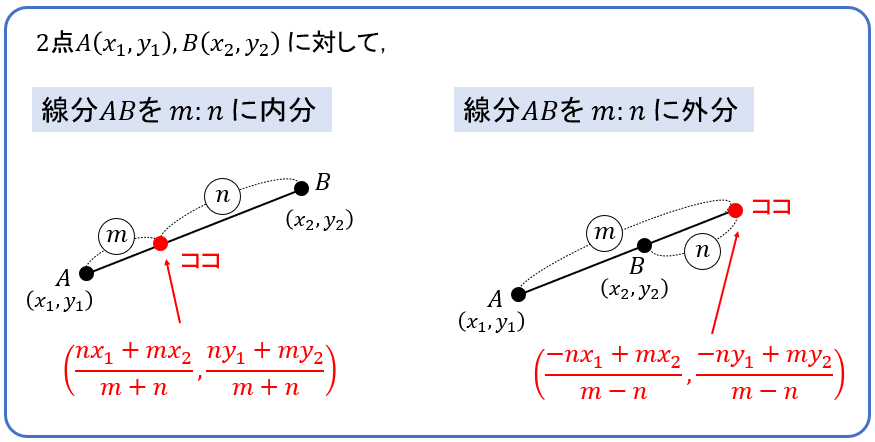
見た目が難しいのでワケわからん!
って思うかもしれませんが、やることはすっごくシンプルで簡単です!
その手順についてイチから見ていきましょう(‘ω’)ノ
今回の内容をサクッと理解したい方はこちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
内分点の座標
【問題】
2点\(A(-3,2), B(4,5)\)を結ぶ線分ABについて、\(2:1\)に内分する点の座標を求めなさい。
上で紹介した公式に当てはめれば求めることができるのですが、公式が覚えにくいので困っちゃいますよね。
なので、次のような流れで求めていきましょう。
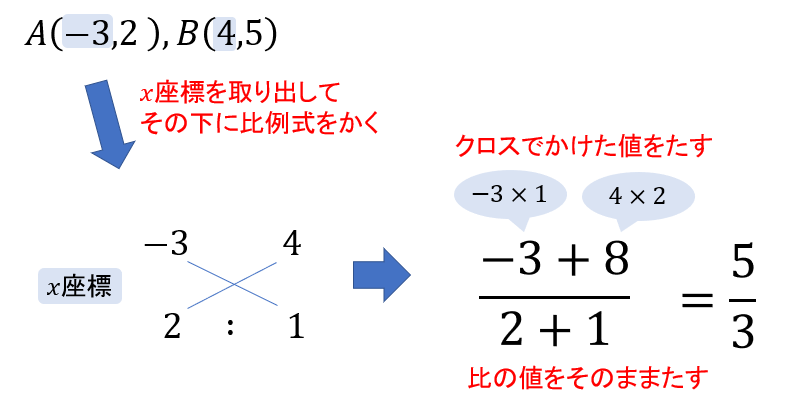
このような手順で計算していけば、勝手に公式が使えちゃいます(‘ω’)ノ
\(x\)座標が求まったら、次は\(y\)座標についても同じようにやっていきましょう。
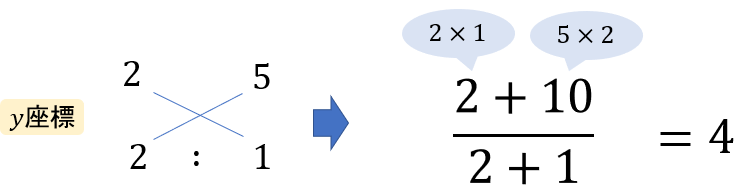

どうかな?手順は理解してもらえましたか?
計算ミスを防ぐためにはていねいに書きながら進めていくのがいいですね!
では、理解を深めるために練習問題にチャレンジしてみましょう。
内分点の練習問題
【問題】次の座標を求めなさい。
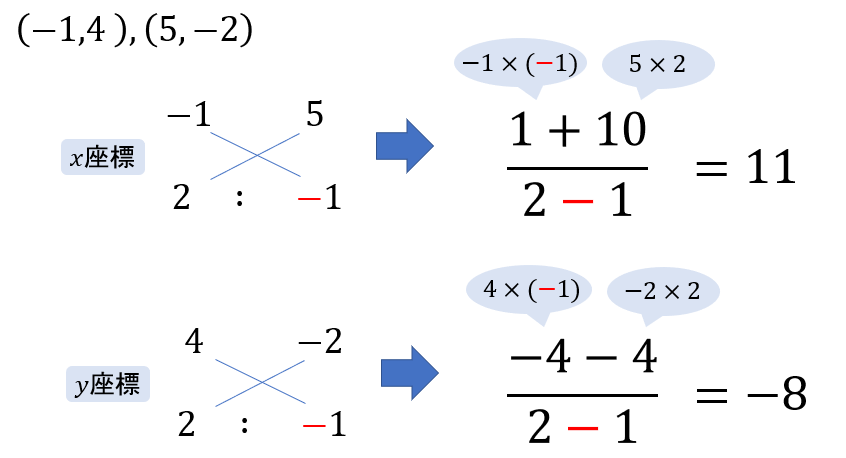
(1) 2点\((-1,4), (5,-2)\) を\(2:1\) に内分する点
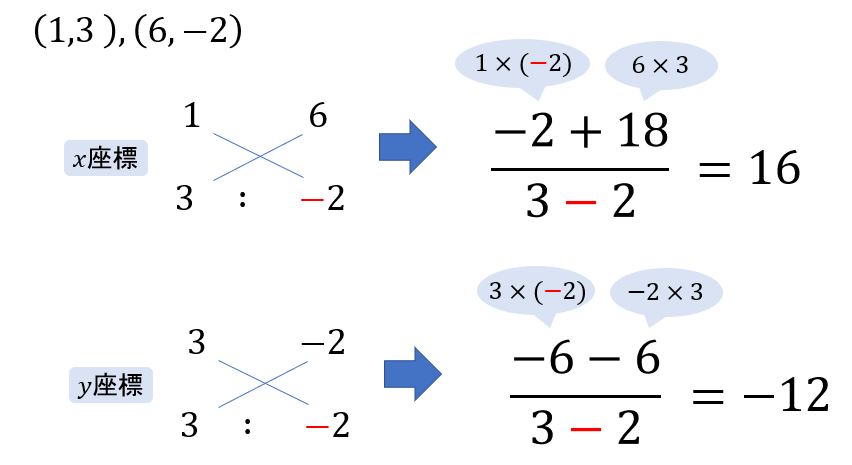
(2) 2点\((1,3), (6,-2)\) を\(3:2\) に内分する点
中点の座標
【問題】
2点\(A(-3,2), B(4,5)\)を結ぶ線分ABについて、中点の座標を求めなさい。
中点とは\(1:1\)に内分する点のことですね。
なので、上で説明した内分のやり方をやってもらえればOKなのですが、もっとシンプルに「中点は足して2で割る」と覚えておけば話が早いです^^

中点は今後いろんな場面で活用することになるのでサクッと求めれるようにしておきましょう!
中点の練習問題
【問題】次の座標を求めなさい。
(1) 2点\((-1,4), (5,-2)\) の中点
(2) 2点\((1,3), (6,-2)\) の中点
外分点の座標
【問題】
2点\(A(-3,2), B(4,5)\)を結ぶ線分ABについて、\(2:1\)に内分する点の座標を求めなさい。
外分の座標を求めるときには、後ろの比の値にマイナスをつけてから内分点と同じやり方で求めていきます。
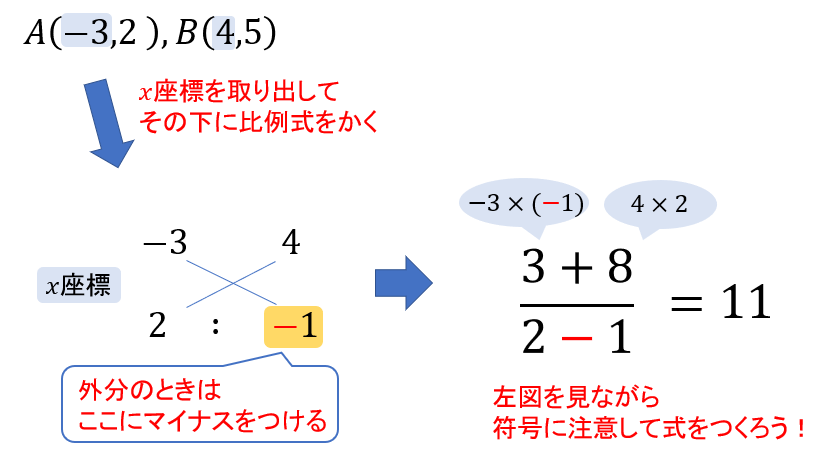
比の値にマイナスがつくことで、分数の式でも符号ミスが起こりやすくなるので注意してくださいね!
\(x\)座標ができたら、次は\(y\)座標についても同じようにやっていきましょう。
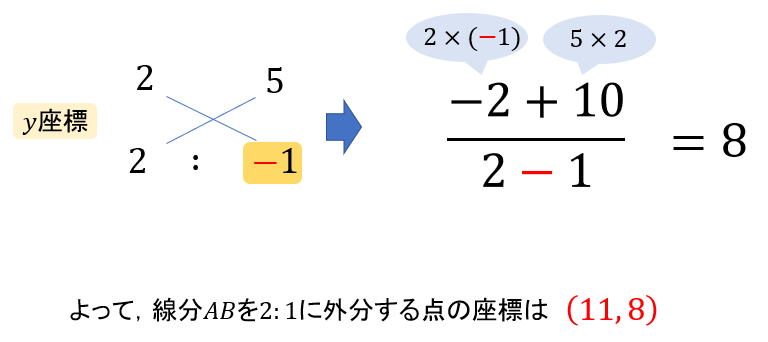
「後ろの比の値にマイナスをつける」
これをしっかりと覚えておけば、やり方は内分のときと同じなのでラクに対処できますね!
では、こちらも練習問題で理解を深めておきましょう。
外分点の練習問題
【問題】次の座標を求めなさい。
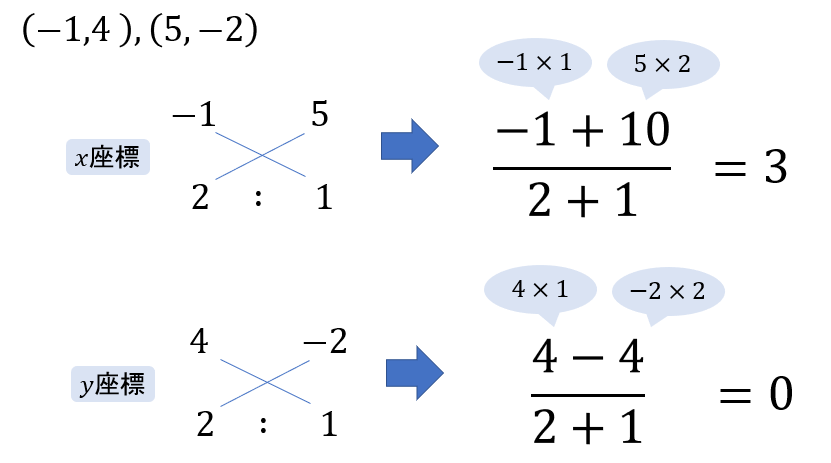
(1) 2点\((-1,4), (5,-2)\) を\(2:1\) に外分する点
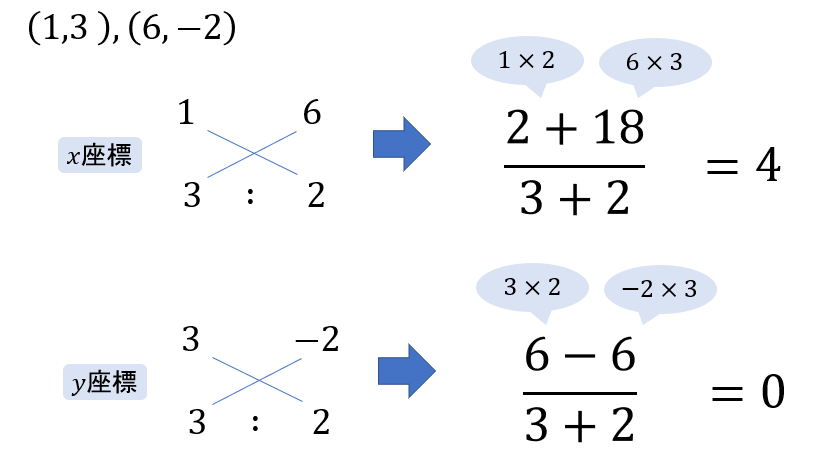
(2) 2点\((1,3), (6,-2)\) を\(3:2\) に外分する点
ちょっとひねったパターン
【問題】
2点\(A(-3,2), B(4,5)\)ついて、点Aが線分EBを2:1に内分するときの点Eの座標を求めなさい。
最後にちょっとひねったタイプの問題にチャレンジ!
ちょっと意味が分かりにくいですが…イメージとしてはこんな感じです。

線分EBを2:1に内分した点がAとなっています。
そのAの座標がわかっているので、それをヒントにしながらEの座標を求めていくようになりますね。
点Eの座標を\((x,y)\)として線分EBを2:1に内分する点の座標を表してみましょう。

この座標が点Aと一致することから、次のように方程式をつくって解いていきます。
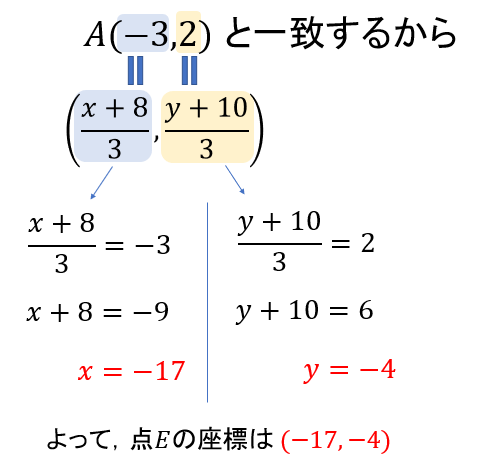
ちょっとややこしい問題でしたが、与えられた情報からていねいに図をかいてみると分かりやすくなりますね^^
まとめ
内分、外分の公式はパッと見ではややこしく感じますが、これまでに紹介してきたような手順をたどってやると、簡単に求めることができますね!
外分のときには「後ろの比の値にマイナスをつける」。
これがすごく重要なのでしっかりと覚えておいてくださいね^^
やり方どうやるんだっけ?と忘れてしまうことがあれば、こちらの動画でサクッと復習するようにしてくださいね(‘ω’)ノ
では、今回も最後までお疲れ様でした(‘ω’)ノ




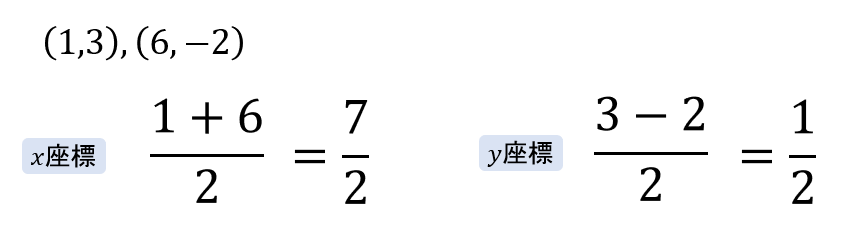














コメントを残す