こんにちは!数スタの小田です。
今回は数学Aの確率の単元からこちらの問題について解説します。
【問題】
ある製品を製造する工場A、Bがあり、Aの製品には5%、Bの製品には3%の不良品が含まれている。A工場の製品200個とB工場の製品300個をよく混ぜ、その中から1個取り出すとき、次の確率を求めなさい。
(1)A工場の不良品である確率
(2)不良品である確率
(3)不良品であったとき、A工場の不良品である確率
【類題】
集団Aでは4%の人が病気Xにかかっている。病気Xを診断する検査で、病気Xにかかっている人が正しく陽性と判定される確率は80%、病気Xにかかっていない人が誤って陽性と判定される確率は10%である。集団Aのある人がこの検査を受けたとき、次の確率を求めなさい。
(1)その人が陽性と判定される確率
(2)陽性と判定されたとき、その人が病気Xにかかっている確率
難しそうな問題ですが、考え方がわかってしまえばサクッと完答できるようになります^^
今回の記事を通して、工場の条件付き確率を一緒にマスターしていきましょう(‘ω’)ノ
サクッと理解したい方は、こちらの動画も参考にしてください!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
工場の不良品についての条件付き確率 考え方
ある製品を製造する工場A、Bがあり、Aの製品には5%、Bの製品には3%の不良品が含まれている。A工場の製品200個とB工場の製品300個をよく混ぜ、その中から1個取り出すとき、次の確率を求めなさい。
(1)A工場の不良品である確率
(2)不良品である確率
(3)不良品であったとき、A工場の不良品である確率
問題を解くにあたって、簡単でOKなのでまずは以下のような図を書いておくといいですよ^^
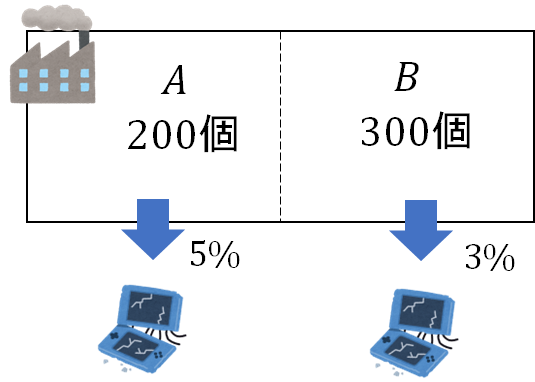
工場A、Bの個数、それぞれに対する不良品の割合をパッと判断できるように書いてくださいね。
(1)A工場の不良品である確率
A工場の不良品を取り出すためには、2つの壁をクリアする必要があります。
1つ目の壁「A工場の製品をとる」
全部で500個、その中でA工場は200個だから、確率は\(\frac{200}{500}\)ですね。
2つ目の壁「それが不良品である」
A工場の製品には5%だけ不良品が含まれているので、不良品をひく確率は5%、つまりは\(\frac{5}{100}\)ですね。
そういうわけで、次のように式を作ればOKです。
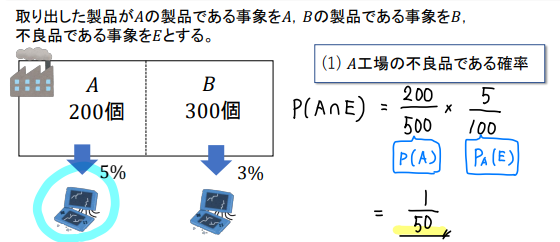
A工場の不良品を取り出すためには…
「A工場の製品をとる必要があって、さらにそれが不良品だから」
という流れで考えてもらえれば、式が作りやすくなりますよね!
答え
$$\frac{1}{50}$$
(2)不良品である確率
取り出した製品が不良品となるのは以下の2パターンが考えられます。
「Aの不良品を取り出す」「Bの不良品を取り出す」
なので、以下のように考えていきましょう。

Bの不良品を取り出す確率については(1)と同じように求めることができるので、
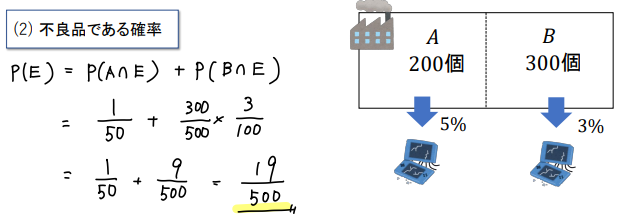
このように求めることができますね!
「不良品を取り出す」といっても、その中にはどんなパターンが含まれているのかを考えるようにしてください。
答え
$$\frac{1}{50}$$
(3)不良品であったとき、A工場である確率
(1)(2)が解けていれば、(3)は楽勝で解けます!
問題文から、このように式を作ります。
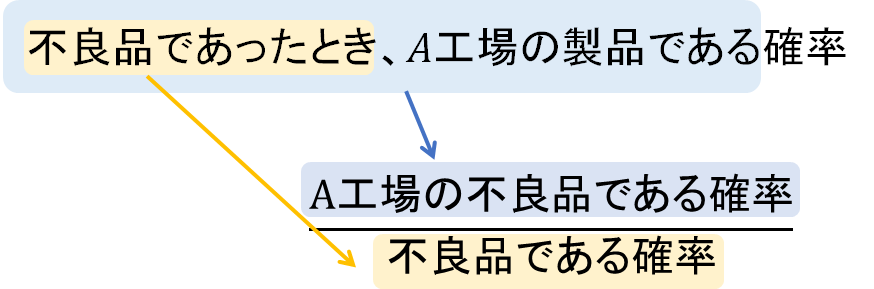
そして、(1)(2)で求めたものをそのまま当てはめればOKです。

答え
$$\frac{10}{19}$$
どうでしょうか。
見た目は難しそうな問題でしたが、やっていることはものすごくシンプルですよね^^
それでは、ちゃんと理解できているかを確かめるために類題を用意しました。
こちらが完答できればバッチリです。では、チャレンジしてみましょう(‘ω’)ノ
【類題】病原菌についての条件付き確率
集団Aでは4%の人が病気Xにかかっている。病気Xを診断する検査で、病気Xにかかっている人が正しく陽性と判定される確率は80%、病気Xにかかっていない人が誤って陽性と判定される確率は10%である。集団Aのある人がこの検査を受けたとき、次の確率を求めなさい。
(1)その人が陽性と判定される確率
(2)陽性と判定されたとき、その人が病気Xにかかっている確率
お疲れ様でした!
類題もしっかりと完答できましたか^^
テストに出やすい問題だと思うので、今回の記事をキッカケに得点UPを達成してもらえると嬉しいです!
あとは学校の問題集などを使って、たくさん練習しといてくださいね。
では、今回は以上!



















コメントを残す