こんにちは!数スタの小田です。
今回は高校数学Ⅰで学習するデータの分析の単元から「中央値のとり得る範囲」についてイチから解説します。
これはちょっとややこしい問題です(^^;)
いろんな場合を考えながら答えを見つけていくのですが、その場合分けが難しい!
なので、どういった手順で進めていけばサクッと答えが出せるのか解説していきますね(‘ω’)ノ
取り上げる問題はこちらです。
【問題】
次のデータにおいて、\(x\)の値がわからないとき、中央値として何通りの値があるうるか求めなさい。ただし、\(x\)の値は正の整数である。

今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
中央値のとりうる値の範囲を求めるやり方
(1)の手順
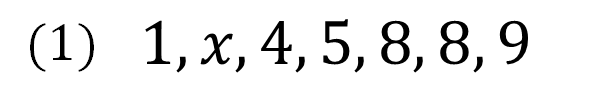
まず、今回は4番目が中央値になることを頭に入れておいてください!
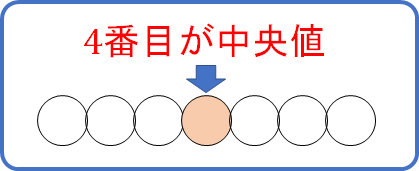
次に\(x\)を除いた数を取り出し、中央値がどのあたりになるのかをチェックします。
すると、5と8の真ん中が中央値のラインとなりますね。

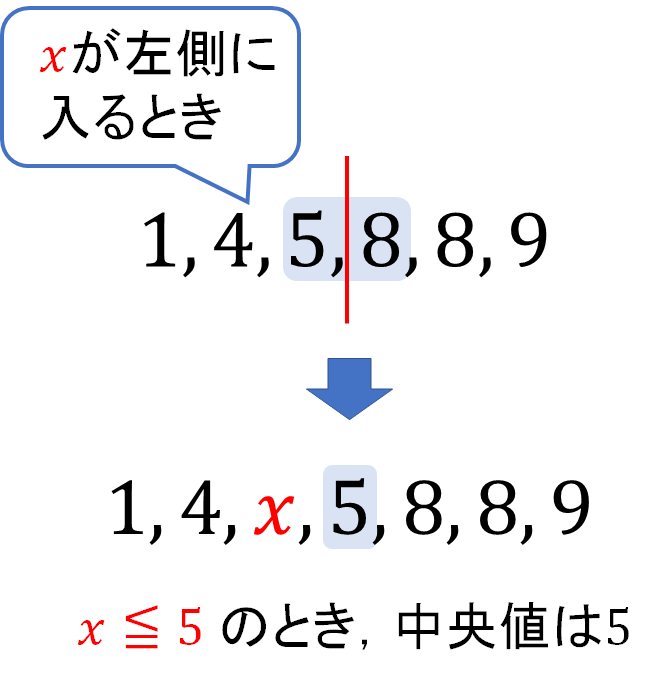
この状態から\(x\)を入れたとき、次のような3パターンの中央値がつくれます。
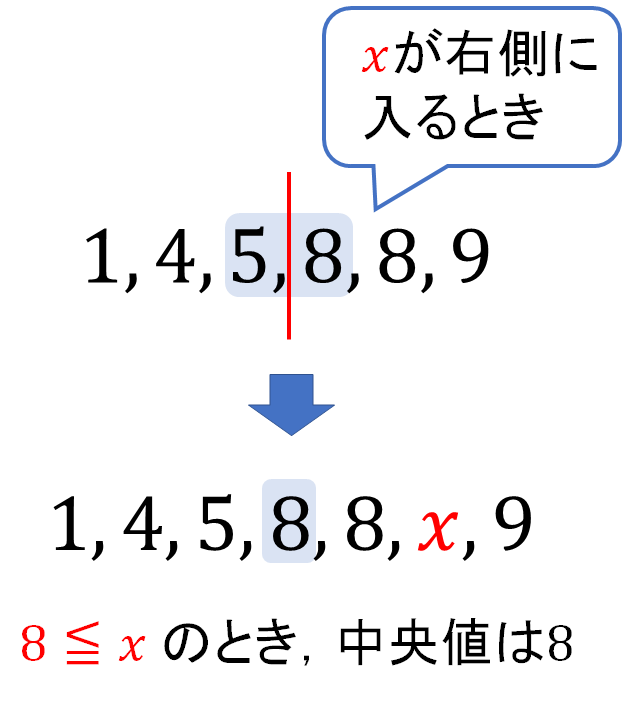

最後の真ん中に入るパターンがちょっとイメージしにくいかもしれませんが、このときは\(x\)の値がそのまま中央値になります。
なので、\(x\)が真ん中に入るときは \(x=6,7\) の2パターンなので、中央値もそのまま6,7の2通りとなります。
よって、中央値は5、6、7、8の合計4通りとなります。
答え
$$4通り$$
このように、\(x\)を取り除いた状態で中央値のラインを決めて、そこから\(x\)を入れていきながら中央値のパターンを探っていくのがおススメです!
(2)の手順
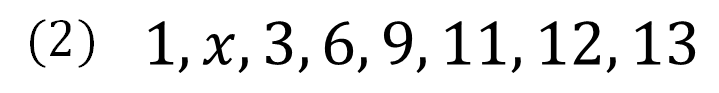
まず、今回は4番目、5番目の平均が中央値になることを頭に入れておいてください!
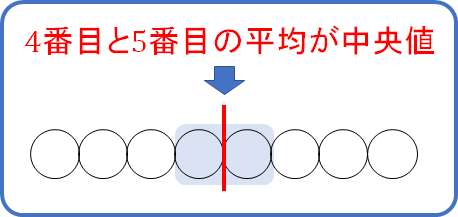
次に\(x\)を除いた数を取り出し、中央値がどのあたりになるのかをチェックします。
すると、9が中央値のラインとなりますね。

この9を基準に考えると、\(x\)を入れたときの中央値のとり方は、
「6と9」「\(x\)と9」「9と11」の平均を考える3パターンであると見つかります!

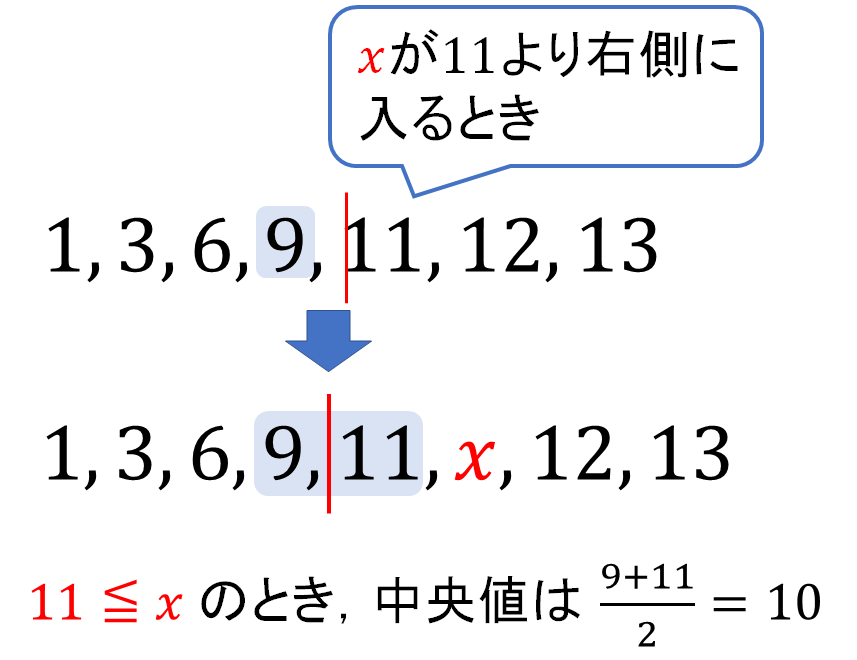
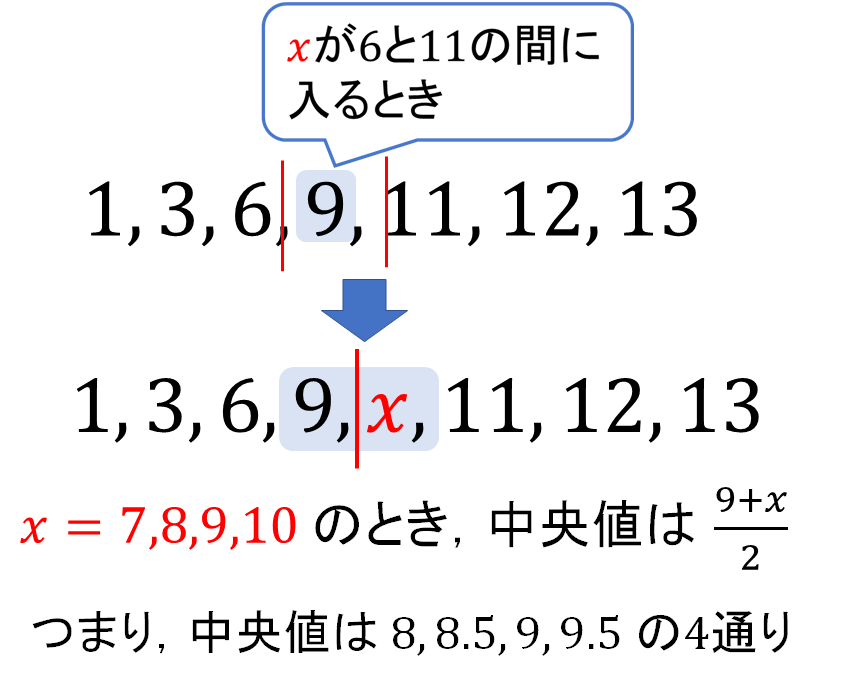
よって、中央値は合計6通りとなります。
答え
$$6通り$$
(3)の手順
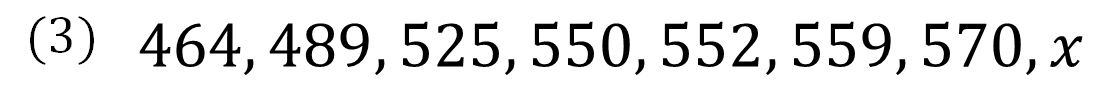
こちらは数が大きくなっていますが、基本的な考え方は(2)と同じです。
4番目と5番目の平均が中央値になることを意識した上で、

\(x\)を取り除いた状態の中央値ラインを探します。

すると、550が中央値のラインとなることがわかります。
この550を基準に考えると、\(x\)を入れたときの中央値のとり方は、
「525と550」「\(x\)と550」「550と552」の平均を考える3パターンであると見つかります!

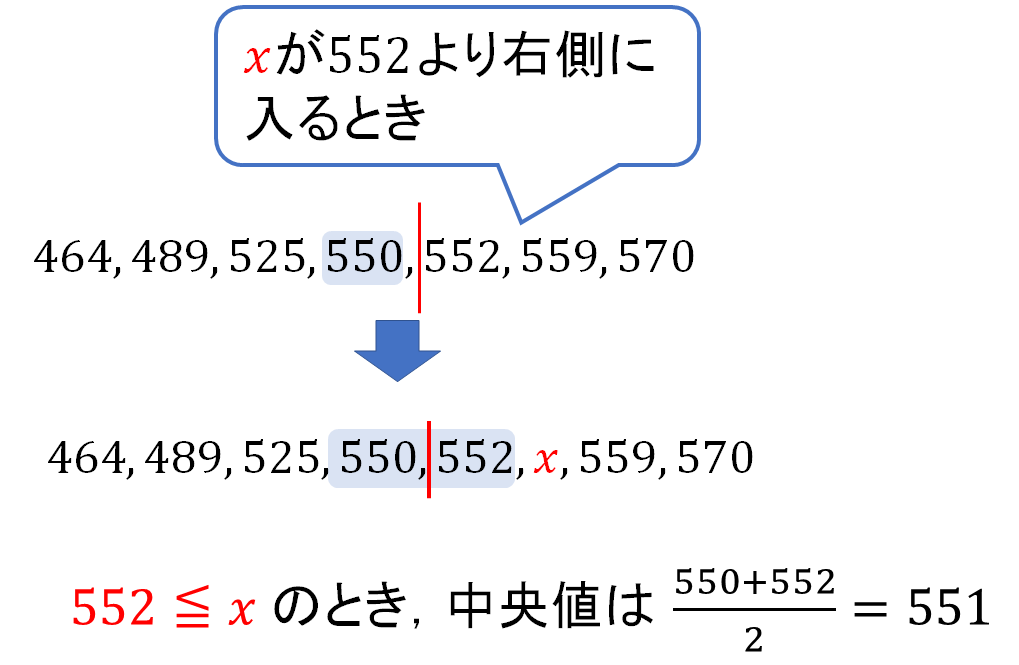
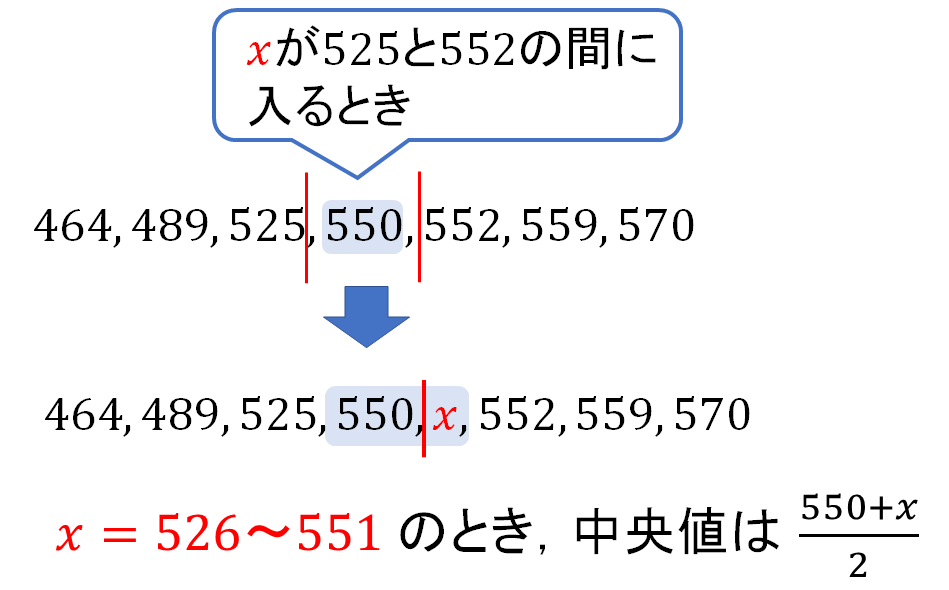
このとき注意することは、526から551の間にいくつの数が入っているかということです。
計算すると、次のような式になります。
$$551-526\color{red}{+1}=26$$
それぞれの数をそのまま引くだけでは1少ない値になってしまうので、最後に「+1」することを忘れないように!
\(x\)の値が26個あるということなので、それにともなって中央値の値も26通り出てくることになります。
よって、中央値は全部で\(1+1+26=28\)ですね!
答え
$$28通り$$
まとめ
お疲れ様でした!
中央値の場合分けについて理解してもらえましたか?
この内容は僕も教えるのに苦労していたのですが、今回紹介したステップで教えるようになってからは生徒さんの理解度もグッと高まってきた印象です!
- xを除いた数で中央値のラインを見つける
- ①の基準をもとに\(x\)を「左、真ん中・右」に入れた3パターンで中央値を考える
では、今回は以上!















コメントを残す