余弦定理とは、三角比の単元で学習するとっても大切な定理の1つです。
余弦定理
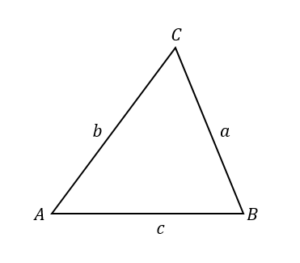
$$a^2=b^2+c^2-2bc\cos A$$
$$b^2=c^2+a^2-2ca\cos B$$
$$c^2=a^2+b^2-2ab\cos C$$
だけど、こんな式がなぜ成り立つの?
ということを正確に理解している人は少ない…
余弦定理の証明は、とっても簡単で5分もあれば理解できちゃうようなものなので、サクッと頭に入れておきましょう。
昨今の入試では、定理の証明なども出題されることがあるので、そういったところで役に立つかもしれませんからね(^^)
余弦定理の証明
三角形の形によって、証明の過程が異なってくるので3つのパターンに分けて考えてみましょう。
【証明】鋭角三角形の場合
次のような鋭角三角形の場合

$$a^2=b^2+c^2-2bc\cos A$$
が成立することを証明します。
まず、頂点Cから辺ABに垂線CHを下すと
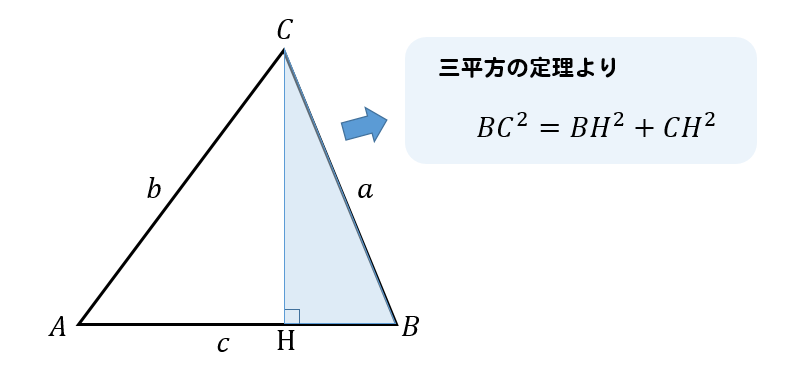
△BCHは直角三角形になるので、三平方の定理より
$$BC^2=BH^2+CH^2$$
という式がつくれます。
次に、角Aを基準に△ACHの直角三角形に注目すると
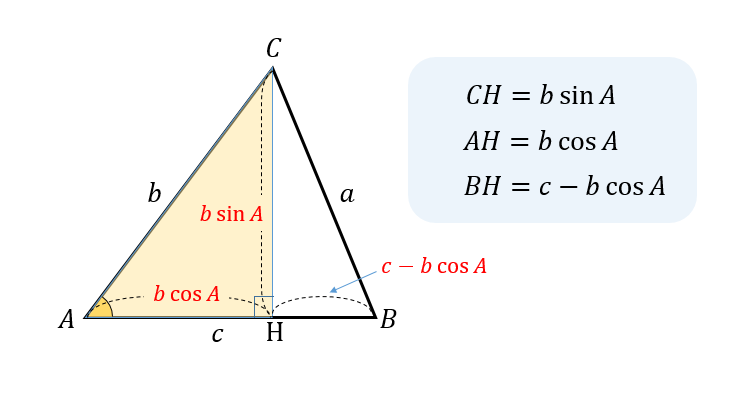
$$AH=b\cos A$$
$$CH=b\sin A$$
$$BH=AB-AH=c-b\cos A$$
と表すことができます。
すると、\(BC, BH, CH\) の大きさがそれぞれ表せたので
三平方の定理で作った\( BC^2=BH^2+CH^2\) の式に代入すると
$$\begin{eqnarray} a^2&=&(c-b\cos A)^2+(b\sin A)^2\\[5pt]a^2&=&c^2-2bc\cos A+b^2\cos^2 A+b^2\sin^2 A\\[5pt]a^2&=&c^2-2bc\cos A+b^2(\cos^2 A+\sin^2 A)\\[5pt]&\color{white}{=}&\sin^2 A+\cos^2 A=1だから\\[5pt]\color{red}{a^2}&\color{red}{=}&\color{red}{ c^2+b^2-2bc\cos A}\end{eqnarray}$$
このようにして、余弦定理の式を証明することができました。
【証明】直角、鈍角三角形の場合①
次のような鋭角三角形の場合(直角の場合も含む)
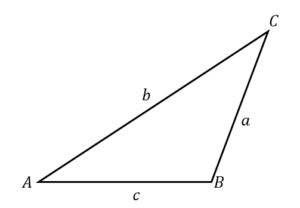
$$a^2=b^2+c^2-2bc\cos A$$
が成立することを証明します。
証明の手順は先ほどと同じです。
頂点Cから垂線CHを下ろし、三平方の定理から式を作ります。
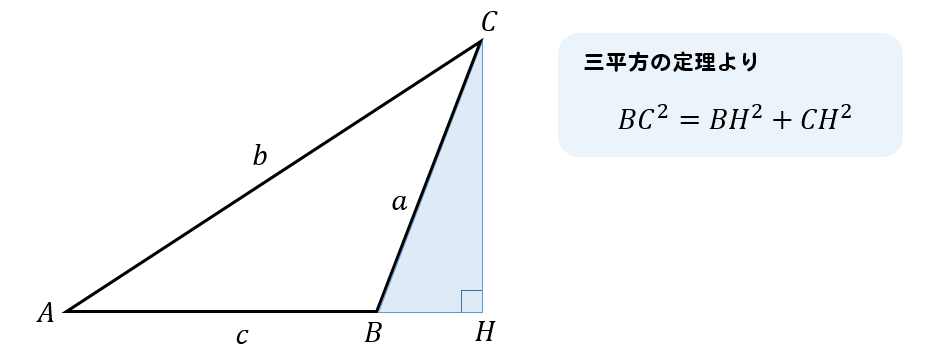
次に△AHCの直角三角形に注目すると
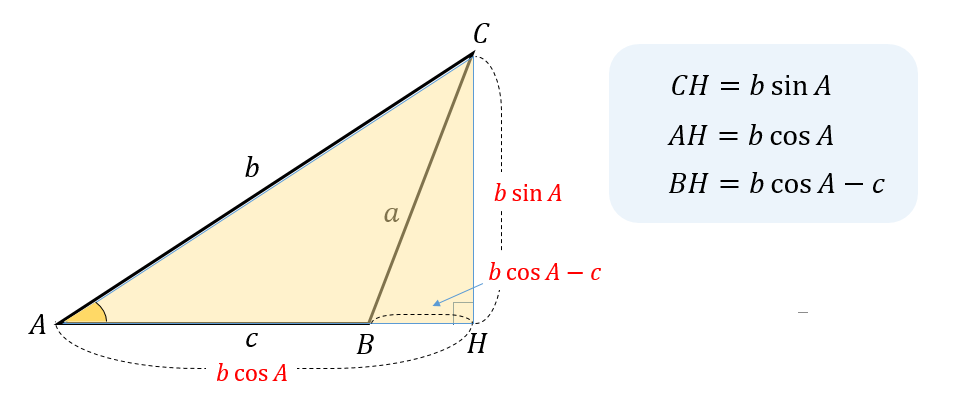
$$AH=b\cos A$$
$$CH=b\sin A$$
$$BH=AH-AB=b\cos A-c$$
と表すことができます。
以上より
$$\begin{eqnarray} a^2&=&(b\cos A-c)^2+(b\sin A)^2\\[5pt]a^2&=&b^2\cos^2 A-2bc\cos A+c^2+b^2\sin^2 A\\[5pt]a^2&=&c^2-2bc\cos A+b^2(\cos^2 A+\sin^2 A)\\[5pt]&\color{white}{=}&\sin^2 A+\cos^2 A=1だから\\[5pt]\color{red}{a^2}&\color{red}{=}&\color{red}{ c^2+b^2-2bc\cos A}\end{eqnarray}$$
このようにして、余弦定理の式を証明することができました。
【証明】直角、鈍角三角形の場合②
次のような鋭角三角形の場合(直角の場合も含む)
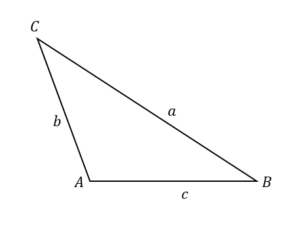
$$a^2=b^2+c^2-2bc\cos A$$
が成立することを証明します。
頂点Cから垂線CHを下ろし、三平方の定理から式を作ります。
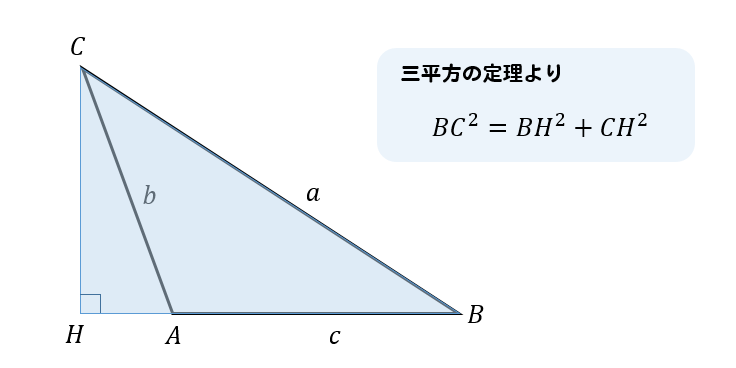
\(\cos ∠CAH=\cos (180-A)=-\cos A\) 、\(\sin ∠CAH=\sin (180-A)=\sin A\) という点に気を付けて
△ACHの直角三角形に注目していきます。
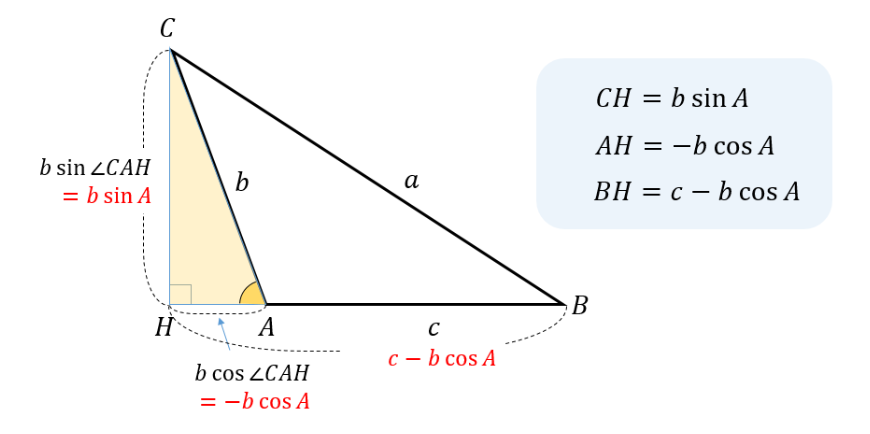
$$AH=-b\cos A$$
$$CH=b\sin A$$
$$BH=AH-AB=c-b\cos A$$
と表すことができます。
以上より
$$\begin{eqnarray} a^2&=&(c-b\cos A)^2+(b\sin A)^2\\[5pt]a^2&=&c^2-2bc\cos A+b^2\cos^2 A+b^2\sin^2 A\\[5pt]a^2&=&c^2-2bc\cos A+b^2(\cos^2 A+\sin^2 A)\\[5pt]&\color{white}{=}&\sin^2 A+\cos^2 A=1だから\\[5pt]\color{red}{a^2}&\color{red}{=}&\color{red}{ c^2+b^2-2bc\cos A}\end{eqnarray}$$
このようにして、余弦定理の式を証明することができました。
よって、どんな形の三角形であっても余弦定理の式が成立することが言えましたね(^^)
直角三角形の辺の大きさは、三角比を使って表し、三平方の定理に当てはめる。
それだけのことでした。
余弦定理から角の大きさを判断
余弦定理の式を深堀することで、その角の大きさを判断することもできるのです。
余弦定理の式を変形すると
$$\begin{eqnarray}a^2&=&b^2+c^2-2bc\cos A \\[5pt]2bc\cos A&=&b^2+c^2-a^2\\[5pt]\cos A&=&\frac{b^2+c^2-a^2}{2bc}\end{eqnarray}$$
このように、\(\cos A=\cdots\) の形にすることができます。
この式を利用することでAの角の大きさについて判断することができます。
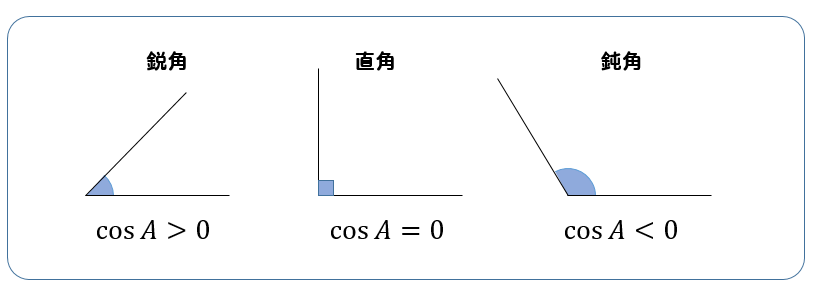
角Aが鋭角の場合、\(\cos A\) の値は正なるはずだから
$$\begin{eqnarray} \cos A &>&0\\[5pt] \frac{b^2+c^2-a^2}{2bc}&>&0\\[5pt]b^2+c^2-a^2&>&0\\[5pt]\color{red}{b^2+c^2}&\color{red}{>}&\color{red}{a^2}\end{eqnarray}$$
という式を作ることができます。
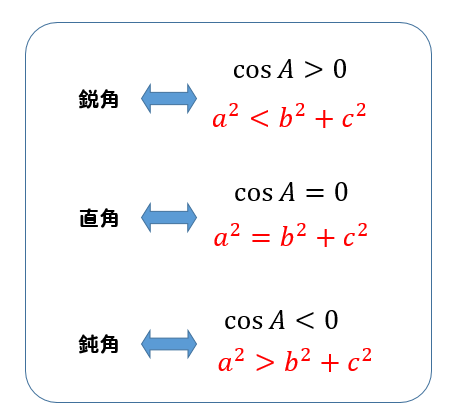
直角、鈍角の場合も同じように式を作ると以下のようになります。
余弦定理の問題を計算
実際に、余弦定理を使ってどのように計算すればよいのかを見ておきましょう。
△ABCにおいて、次のものを求めよ。
$$a=4, b=\sqrt{2}, C=45° のとき、c$$
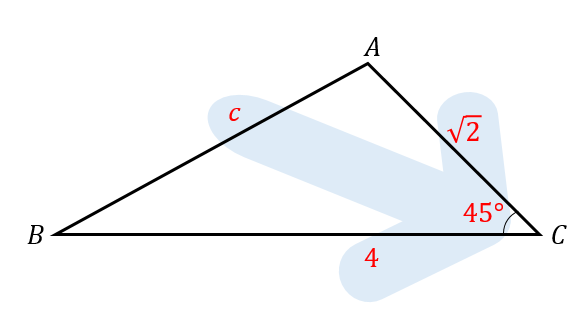
余弦定理は、上の図のように矢印の位置にある辺や角の大きさを使います。
$$\begin{eqnarray}c^2&=&4^2+(\sqrt{2})^2-2\cdot 4\cdot \sqrt{2}\cos 45°\\[5pt]c^2&=&16+2-8\sqrt{2}\cdot \frac{1}{\sqrt{2}}\\[5pt]c^2&=&10\\[5pt]c>0&\color{white}{=}&だから\\[5pt]c&=&\sqrt{10} \end{eqnarray}$$
他にも余弦定理を使った演習をしたい場合は
>【余弦定理の公式】覚え方はどうする?角度の求め方などを解説!
こちらの記事をご参考ください。
【余弦定理の証明】まとめ!
以上!
余弦定理の証明についてでした。
定理の証明などは、問題を解く上では必要ないことが多いですが、知っておくだけで知識が深まりいろいろな場面で活用できることが多いです。
今回の記事がみなさんのお役に立てることを願っています(^^)
余弦定理

$$a^2=b^2+c^2-2bc\cos A$$
$$b^2=c^2+a^2-2ca\cos B$$
$$c^2=a^2+b^2-2ab\cos C$$
















コメントを残す