こんにちは!数スタの小田です。
今回は中3で学習する式の展開の単元から「置き換えを利用した展開」について取り上げます。
ここは式の展開のラスボスですね!置き換えの基本からマイナスでくくる応用パターンなど、テストに出そうなものを全部まとめて解説していきますので、この記事を通して置き換えマスターになっちゃいましょう(‘ω’)ノ
最後には演習プリントも用意しているので、ぜひ活用してくださいね。
では、今回取り上げる問題はこちら!
【練習問題】次の式を展開しなさい。
(1)\((a+b-2)(a+b+2)\)
(2)\((a+b+c)^2\)
(3)\((3a+b-3)(3a-b+3)\)
順に解き方を確認していきましょう。
サクッと理解した方はこちらの動画も参考にしてください^^
(1)置き換えの基本パターン

まずはかっこ内にある同じパーツを探しましょう。
今回であればパッと見て「\(a+b\)」が共通していることに気が付きますね。そして、そこをまとめて文字で置き換えちゃいます。このとき、文字は何を使ってもよいのですが\(A、M、X\)といった文字で置き換えることが多いですね!

置き換えを利用すると、かっこ内がスッキリとして展開の計算がラクになります。

\(X^2-4\) まで計算できたら、置き換えをもとに戻していきましょう。このとき必ず「かっこをつけて戻す」ということを意識してください。ここは符号のミスが起こりやすいので、かっこを忘れないように!
そして、元に戻した部分を計算すれば完成です^^
では、置き換えの基本パターンがしっかりと身についているか練習してみましょう。
【練習問題】次の式を展開しなさい。
$$(x-y-2)(x-y-9)$$
(2)かっこの中に3つあるパターン

かっこ内にある2つの項をひとかたまりとして置き換えます。(今回は\(a+b\)で置き換えていますが、\(b+c\)や\(a+c\)を置き換えてもOK)

そうすることで、かっこ内の項が2つになり、これまでに学習してきた乗法公式が利用できますね!

今回も置き換えを戻すときには、かっこをつけるように!
では、かっこの中に3つあるパターンがしっかりと身についているか練習してみましょう。
【練習問題】次の式を展開しなさい。
$$(x+y-5)^2$$
(3)マイナスでくくって符号を変えるパターン

かっこ内に同じ項を探すと…\(3a\)の1つだけしかありません。このままでは置き換えができず困ってしまいますね。
ですが、よーく見てみると \(b\)と\(-b\)、\(-3\)と\(3\)はそれぞれ符号が違っているだけです。
ここに注目することで

このように同じパーツを作ってあげることができるんです!
今回のように「同じものが見つからないなぁ…だけど、符号違いになってるものが2つあるぞ!」というときにはマイナスでくくって同じパーツを見つけるという流れを活用してください。
あとは置き換えを利用してこれまでと同じ流れで計算していきましょう。
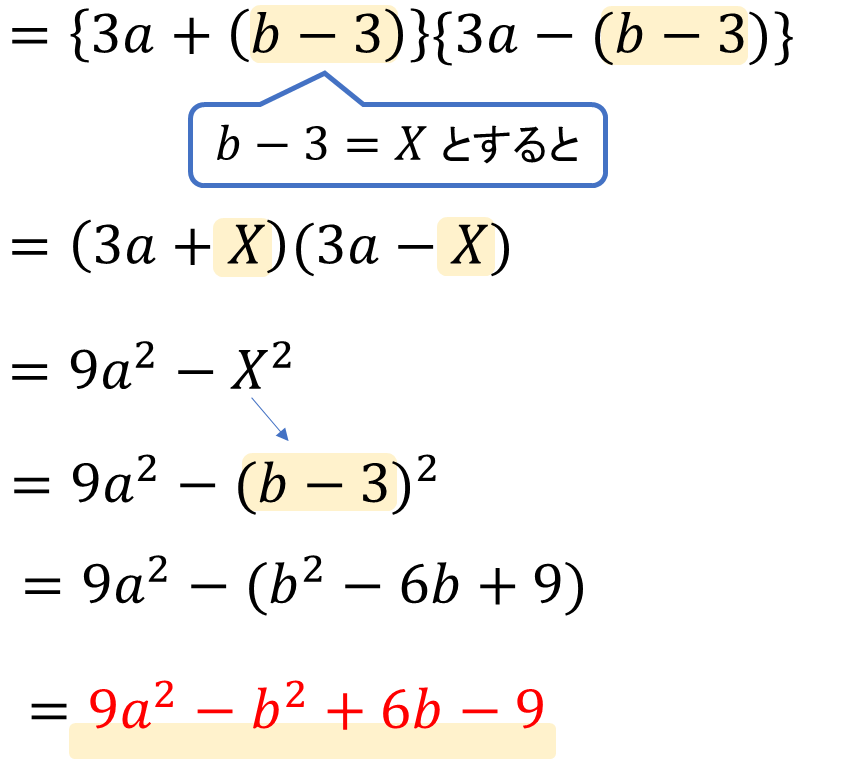
では、マイナスでくくって符号を変えるパターンがしっかりと身についているか練習してみましょう。
【練習問題】次の式を展開しなさい。
$$(a+2b+3c)(a-2b-3c)$$
練習問題(学習プリントつき)
これまではパターン別に練習したので解きやすかった思いますが、ここからはランダム演習です。自分でパターンを判別しながら解いていきましょう。これが完璧になれば置き換えの展開はバッチリです!
学習プリントも用意しました。このページをご覧になっている保護者の方は、このプリントを印刷してお子さんの自宅学習の課題として活用してください。
【練習問題】次の式を展開しなさい。
(1)\((4a+7b-3)(4a-3)\)
(2)\((a+b-1)^2\)
(3)\((x-4y-2)(x+4y+2)\)
(4)\((x-7y+5)^2\)
(5)\((x-3y+2)(x+3y+2)\)
(6)\((x+2y-3)(x-2y+3)\)
【中3向け】入試基礎アップ講座
お疲れさまでした!置き換えの展開はバッチリになりましたか?
定期テストだけでなく、高校入試でもよく出てくる計算なので今のうちにしっかりと仕上げておきましょうね^^
さて、今回の内容は定期テスト対策として取り組んでいる方が多いと思いますが、中3生は早めの受験対策が必須です!
数スタでは高校入試対策の課題をたくさん用意しており、メルマガ講座という形で課題を順次お届けしています。毎年2000名ほどの受験生にご活用いただき、たくさんの合格報告をいただいています^^
無料で活用いただける講座なので気軽にご登録くださいね!




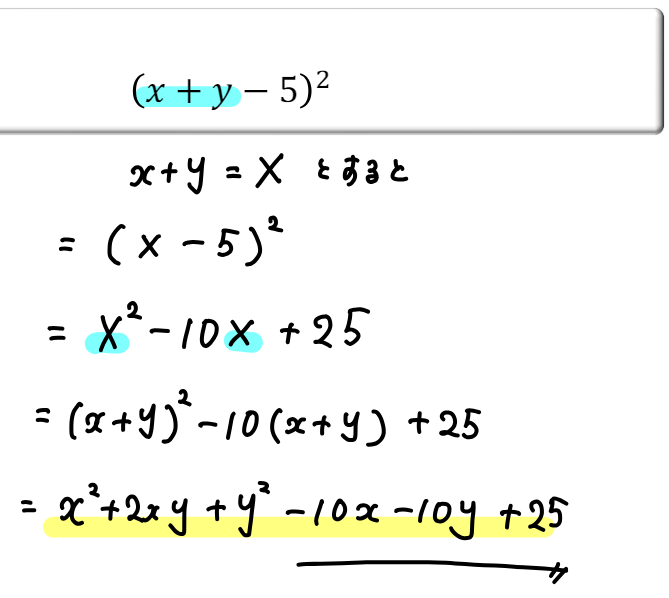



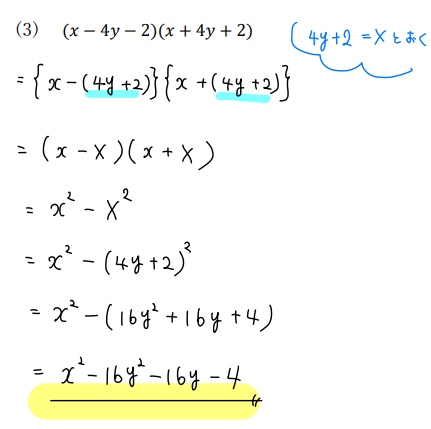

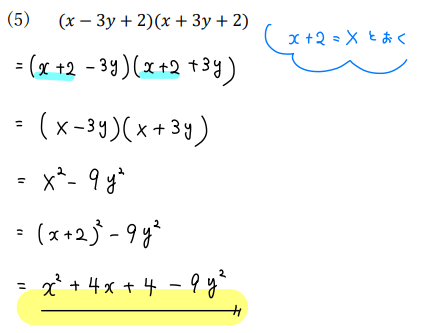
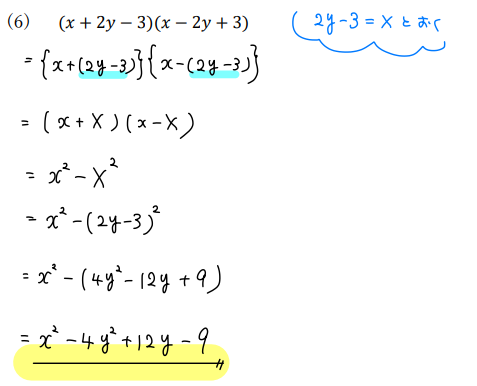













コメントを残す