数スタの小田です!
今回は高校数学Ⅱで学習する図形と方程式の単元から「対称な点の座標」についてイチから解説していきます!
取り上げる問題はこちらです。
【問題①】
点\(P(-2,3)\)に大した次のような点の座標を求めなさい。
(1) \(x\)軸に関して対称な点
(2) \(y\)軸に関して対称な点
(3) 原点に関して対称な点
【問題②】
点\(A(-3,2)\)に関して、点\(P(0,-4)\)と対称な点の座標
今回の内容をサクッと理解したい方はこちらの動画もおススメです^^
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
x軸に関して対称な点の座標
【問題①】
点\(P(-2,3)\)に大した次のような点の座標を求めなさい。
(1) \(x\)軸に関して対称な点
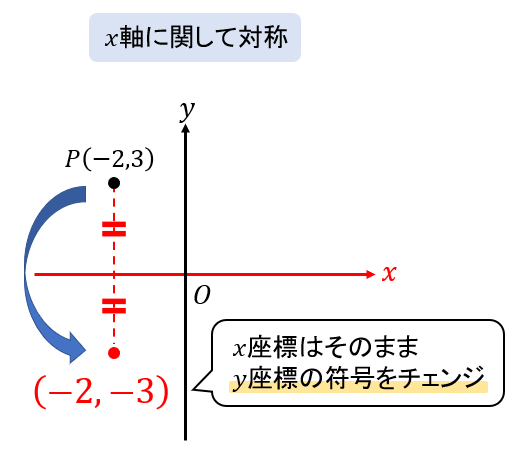
\(x\)軸に関して対称というのは、\(x\)軸(ヨコ)を折り目としてパタンと折り返した場所になります。
つまり、横の位置には変化がなく、縦がパタンと軸の反対側になるってことなので、このように覚えておきましょう!

y軸に関して対称な点の座標
【問題①】
点\(P(-2,3)\)に大した次のような点の座標を求めなさい。
(2) \(y\)軸に関して対称な点
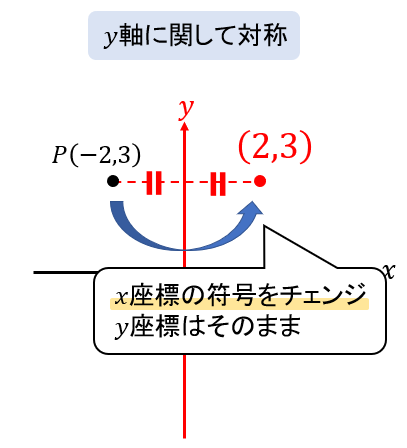
\(y\)軸に関して対称というのは、\(y\)軸(タテ)を折り目としてパタンと折り返した場所になります。
つまり、縦の位置には変化がなく、横がパタンと軸の反対側になるってことなので、このように覚えておきましょう!

原点に関して対称な点の座標
【問題①】
点\(P(-2,3)\)に大した次のような点の座標を求めなさい。
(3) 原点に関して対称な点
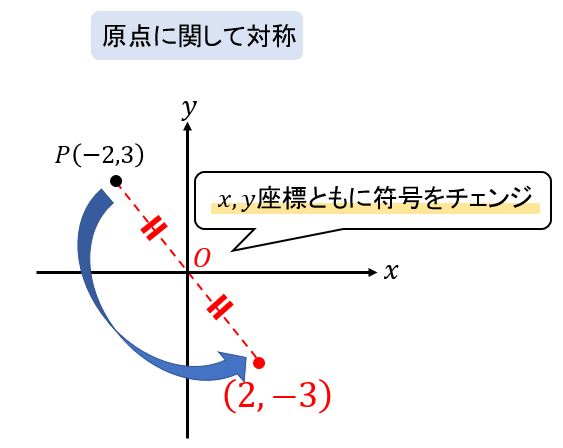
原点に関して対称というのは、パタンと斜めに折り返した位置になります。
つまり、縦、横ともに軸の反対側になるってことなので、このように覚えておきましょう!

ある点に関して対称な点の座標
【問題②】
点\(A(-3,2)\)に関して、点\(P(0,-4)\)と対称な点の座標
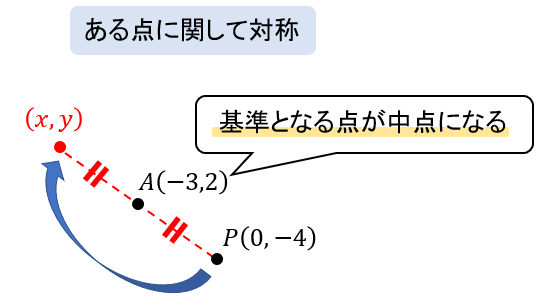
軸ではなく、ある点に関して対称な…ときたときには一発で座標を求めることができません。
なので、求めたい座標を\((x,y)\)として、方程式をつくって解いていきましょう。
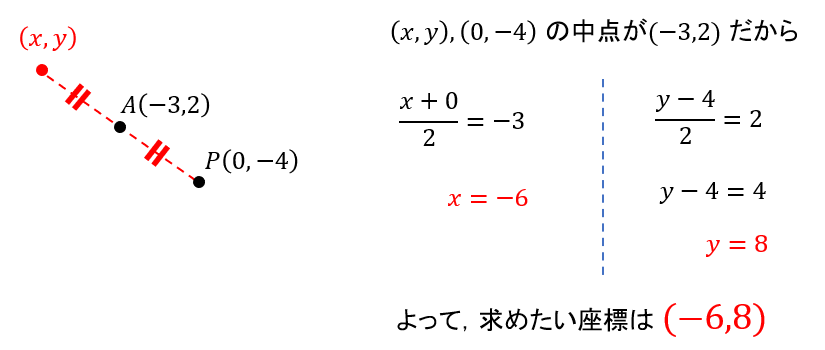
まとめ
では最後に対称な点のポイントをまとめておきますね!
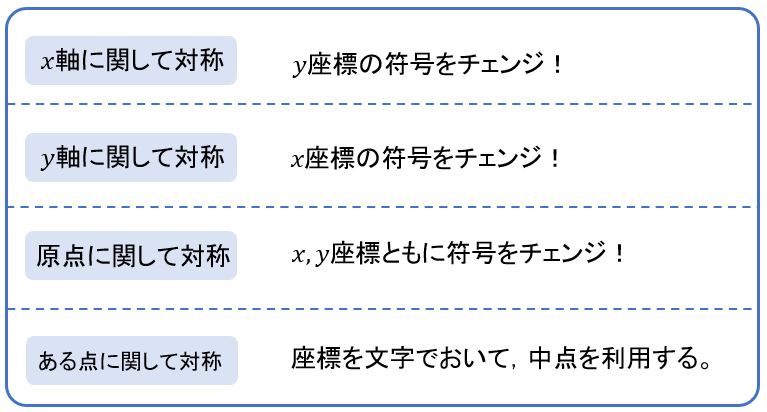
どっちの符号をチェンジするんだっけ…?と忘れてしまったら、グラフをかいて確かめてみるとすぐに思い出せますよね!
簡単な問題なので落ち着いて対処していきましょう(‘ω’)ノ
では、今回は以上!


















コメントを残す