高校数学で学習する「必要十分条件」ってなんなの？
あんまり意味が分かっていないかも…という方が多いです。
この記事にたどり着いた方もそんな悩みを抱いた1人なのでしょう。
というわけで、今回の記事では難しい話は抜きで
必要十分条件についてサクッと理解してもらいます。
十分条件とは
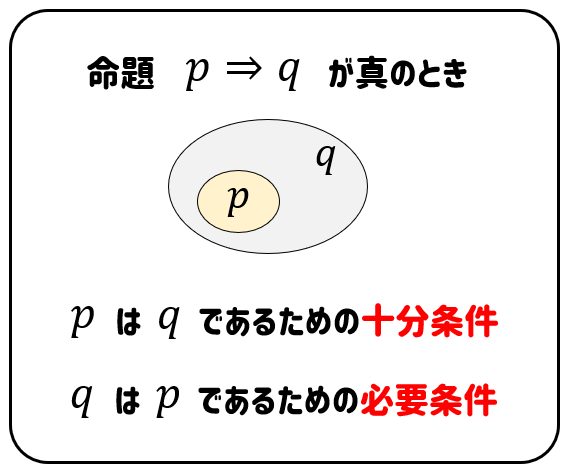
命題「\(p \rightarrow q\)」が真のとき
\(p\)は\(q\)であるための十分条件という。
では、十分条件とはどういうイメージなのか具体例で考えてみましょう。
「\(p\)」大阪に住んでいる。
「\(q\)」日本に住んでいる。
という2つの条件で考えると、このような関係性になっています。
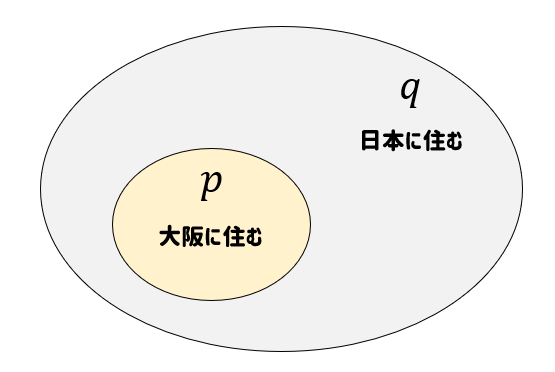
つまり、条件\(p\)（大阪に住む）は条件\(q\)（日本に住む）の中にすっぽり入っていることになります。
だって大阪に住んでいるってことは、日本にも住んでることになるもんね。
このとき、すっぽり入り込んでいる\(p\)（大阪に住む）という条件に注目すると
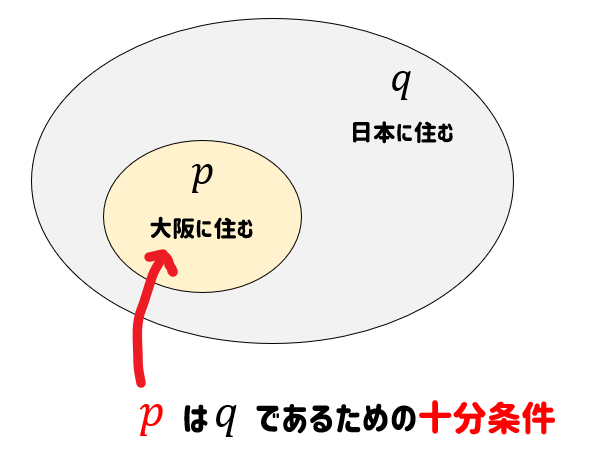
これを十分条件といいます。
大阪に住む（\(p\)）ってことは、十分に日本にも住んでる（\(q\)）ことになるよね。
って考えてみると分かりやすいかもしれませんね。
注目している条件が、もう一方の条件にすっぽりと入れることができるかどうか。
これが十分条件だね。
【例】
\(a=1\)は、\(a>0\)であるための十分条件である。
\(a=1\)という条件は、すっぽりと\(a>0\)の中に入れることができるよね。
入れることができるんだから十分条件だってことだよ。
必要条件とは
命題「\(p \rightarrow q\)」が真のとき
\(q\)は\(p\)であるための必要条件という。
先ほどと同じ条件で考えてみましょう。
「\(p\)」大阪に住んでいる。
「\(q\)」日本に住んでいる。
このとき、\(p\)を包み込んでいる\(q\)（日本に住む）という条件に注目すると
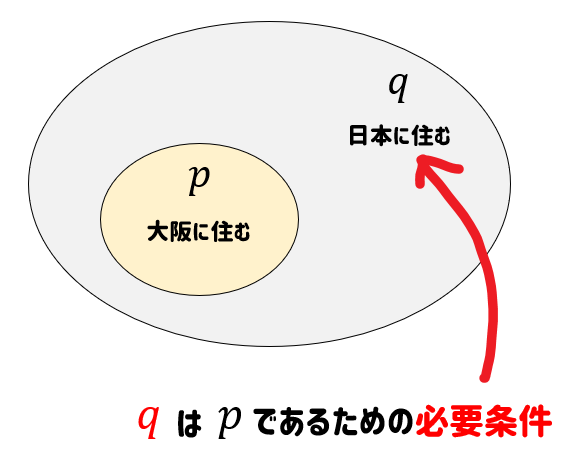
これを必要条件といいます。
日本に住む（\(q\)）ってことは、大阪に住む（\(p\)）ためには必要なこと。
ってイメージしておくといいね！
注目している条件が、もう一方の条件をすべて受け止めることができるかどうか。
これが必要条件だね。
【例】
\(a>0\)は、\(a=1\)であるための必要条件である。
\(a>0\)という条件は、\(a=1\)を受け止めることができます。
すべて受け止めることができるなら必要条件ってことだね。
必要十分条件とは
命題「\(p \rightarrow q\)」「\(q \rightarrow p\)」がそれぞれ真のとき
\(p\)は\(q\)であるための必要十分条件という。
必要条件、十分条件それぞれを満たす場合には
あわせて必要十分条件といいますよーって話だね。
ここからは数学の問題を例にしながら確認していきましょう。
次の☐内に「必要」「十分」「必要十分」のうち適するものを入れよ。
\(x=3\)は、\(x^2=9\)であるための☐条件
\(x=3\)という条件を\(x^2=9\)の中に入れることができれば十分条件。
\(x=3\)という条件が\(x^2=9\)をすべて受け止めることができれば必要条件。
どちらも満たせば必要十分条件ということになります。
まず、\(x^2=9\)が\(x=3,-3\)を表しているということを明らかにしておくと考えやすくなりますね。
するとこんな感じです。
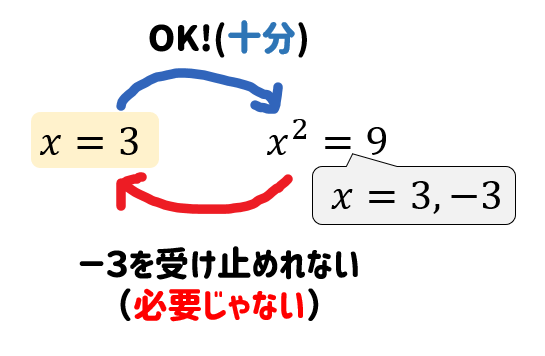
つまり、答えは十分条件ということになります。
このように、「入れれるか（十分）」「受け止めれるか（必要）」をそれぞれ調べることによって、どんな条件になるのかを求めることができます。
次のことをイメージして覚えておくと良いでしょう。
まとめ！
必要十分条件の仕組みは理解してもらえましたでしょうか？
仕組みが分かったら、あとは練習問題を解きながら
出題パターンを知り、知識をつけていきましょう。
出題される問題には一定の傾向があるので
それを掴んでしまえば簡単に解けるようになりますよ(^^)
まぁ、それを掴むためにはひたすら練習あるのみなんだけどね。
ファイトだぞ(/・ω・)/
ありがとうございます。とてもわかりやすかったです。