こんにちは!数スタの小田です。
今回は高校数学Aで学習する図形の単元から「接線の長さ」について取り上げます。
出題されるのは「三角形に内接する円」「共通接線」の2パターンですね!
それぞれの考え方をマスターしていきましょう(‘ω’)ノ
【問題①】三角形に内接する円
△ABCにおいて、この三角形の内接円と各辺との接点をP、Q、Rとするとき、次の問いに答えなさい。
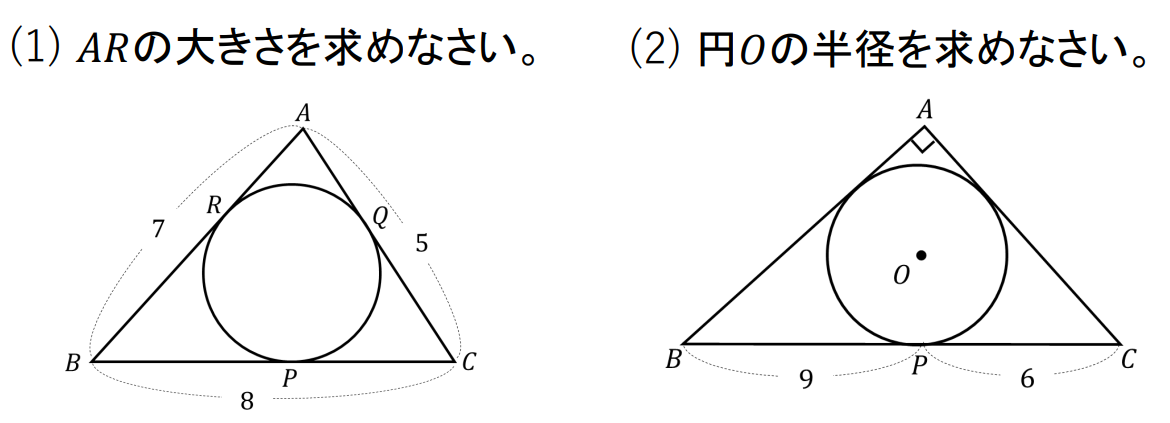
【問題②】共通接線
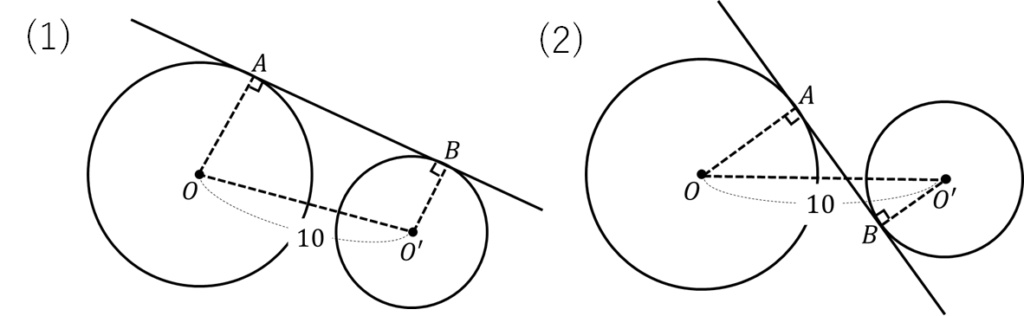
直線ABは2円O、O’にそれぞれ点A、Bで接している。円O、O’の半径が5、3で\(OO’=10\)であるとき、線分ABの長さを求めなさい。
サクッと理解したい方は、こちらの動画も参考にしてください!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
【問題①】接線の長さの求め方
△ABCにおいて、この三角形の内接円と各辺との接点をP、Q、Rとするとき、次の問いに答えなさい。

この問題を解くためのポイントをおさえておきましょう!
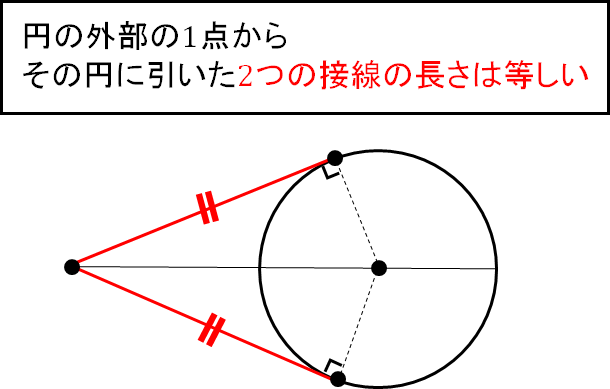
つまり、今回のような三角形と内接円においては次の部分が等しくなります。
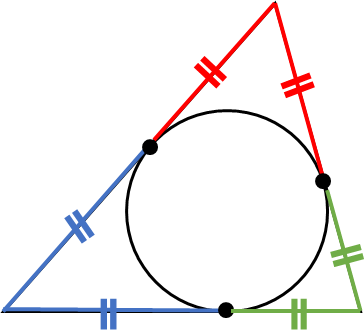
(1)の解説 等しい長さに注目
このことを用いて考えると、(1)は次のように解くことができます。
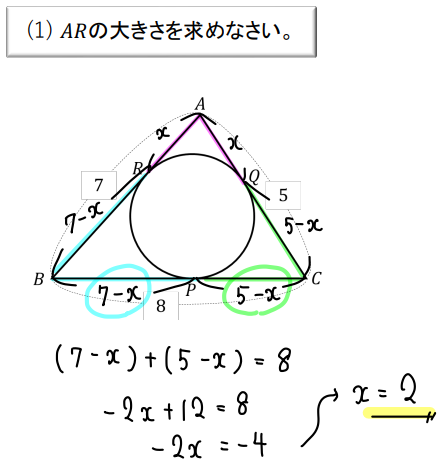
求めたい\(AR\)の長さを\(x\)とする。
すると、\(RB=7-AR=7-x\) と表せますね。
次に接線の性質を用いて、\(BP=RB=7-x\) と表せます。
また、\(AQ=AR=x\) より、先ほどと同じように長さを辿っていくと、\(CP=5-x\) と表せます。
最後に辺\(BC\)に注目すると、
$$\begin{eqnarray}BC&=&8\\[5pt]BP+PC&=&8\\[5pt](7-x)+(5-x)&=&8\\[5pt]-2x+12&=&8\\[5pt]-2x&=&-4\\[5pt]x&=&2\end{eqnarray}$$
このように\(AR\)の長さを求めることができます。
求めたい長さを\(x\)として、そこから長さを辿っていくって感じですね^^
ちなみに今回は文字は\(x\)のみを使いましたが、\(x,y,z\)を使って次のように解くこともできます。
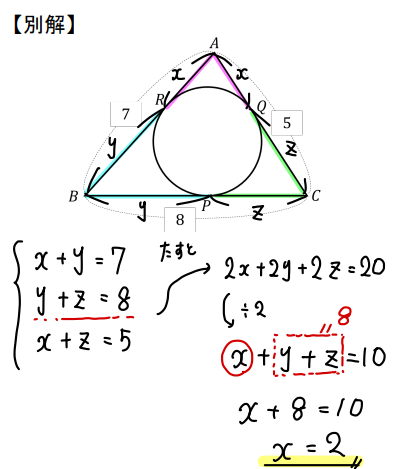
各辺ごとに式をつくって、それらをすべて足して \(2x+2y+2z=20 ⇒ x+y+z=10\) という関係式をつくる。
求めたいのは\(x\)の値なので、ジャマものである\(y,z\)を消すために、\(y+z=8\)を代入して、\(x\)を求めるといった流れです。
どっちのやり方がラクそうですかね?個人的には最初に取り上げた\(x\)だけで解いていく方が好みかな!
だって…文字がたくさん出てくるとなんかややこしいんだもん(^^;)
答え
$$(1)AR=2$$
(2)の解説 補助線を活用
まずは円の中心から接点に向かって補助線を引きます。
半径を\(r\)として、下の図のように半径を三角形の辺上にスライドさせましょう。
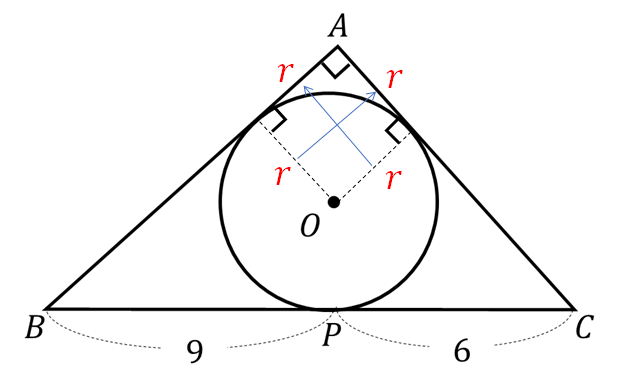
すると、三角形の3辺がそれぞれ\(r+9, r+6, 15 \)と表せます。
そして、直角三角形なので三平方の定理が使えますね!
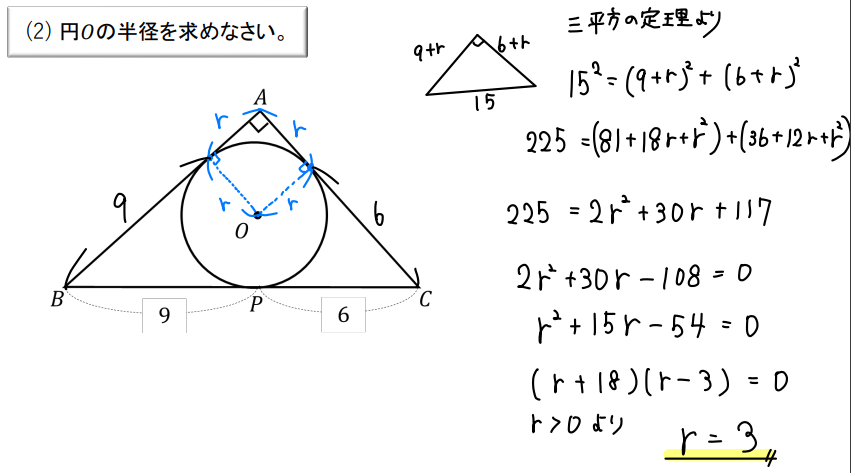
ちょっと計算が大変ですけど…気合いで乗り切ってください!
答え
$$(2) 半径 3$$
【問題②】共通接線の長さの求め方
【問題②】共通接線
直線ABは2円O、O’にそれぞれ点A、Bで接している。円O、O’の半径が5、3で\(OO’=10\)であるとき、線分ABの長さを求めなさい。

ここでは補助線を引いて、直角三角形をつくるのがポイントです!
(1)の解説 補助線を引いて等しい長さを見つける
まずは赤マーカーの部分に補助線をひき、半径3、ABの長さをスライドさせていきます。(補助線をひくことで長方形ができるので、それぞれ対辺の長さが等しい)
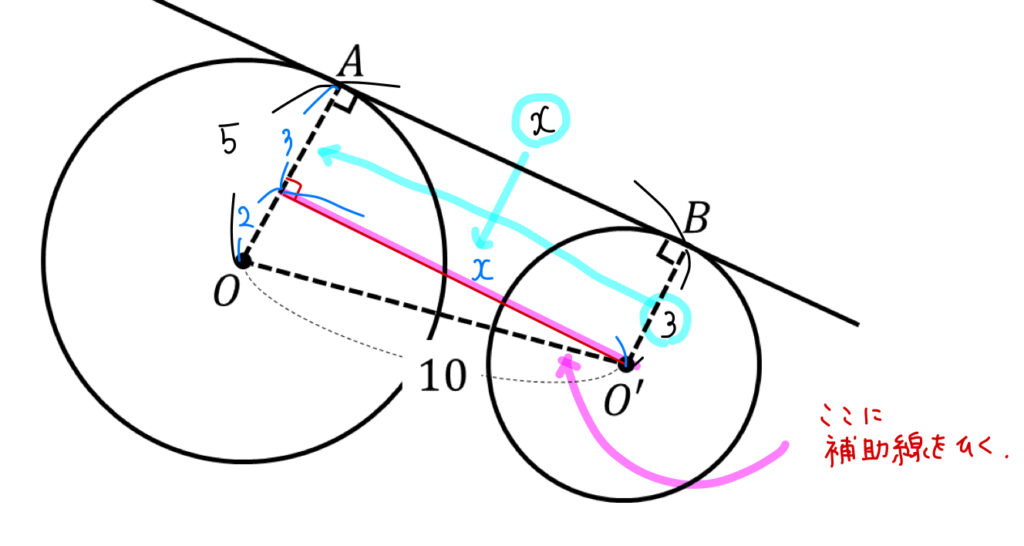
そこから直角三角形に注目して、三平方の定理からABの長さを求めましょう。
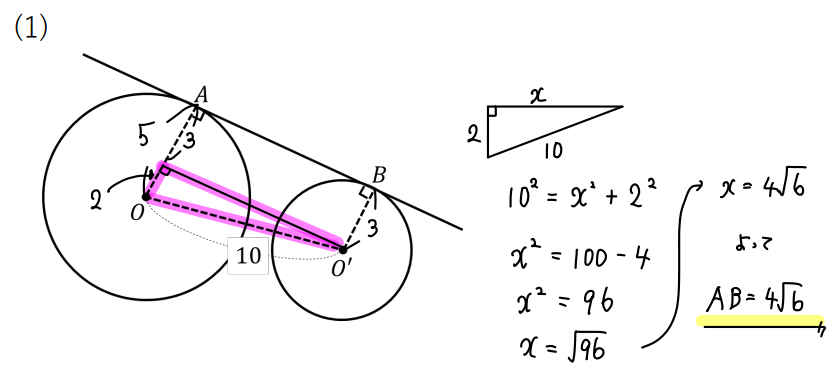
答え
$$(1) 4\sqrt{6}$$
(2)の解説 補助線を引いて等しい長さを見つける
まずは赤マーカーの部分に補助線をひき、半径5、ABの長さをスライドさせていきます。(補助線をひくことで長方形ができるので、それぞれ対辺の長さが等しい)
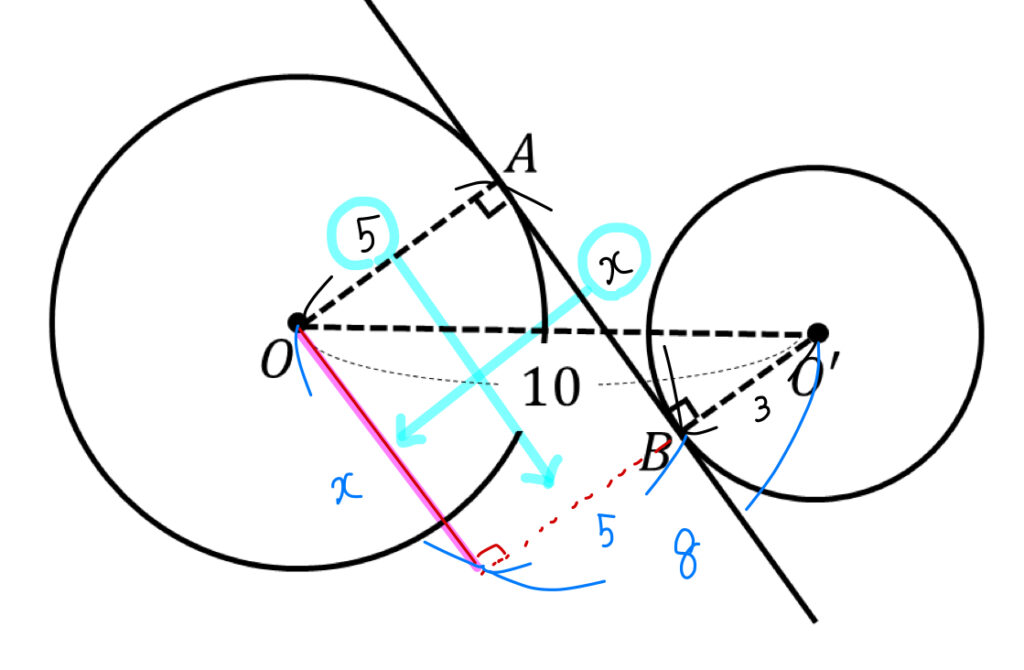
そこから直角三角形に注目して、三平方の定理からABの長さを求めましょう。

答え
$$(2) 6$$
共通接線については補助線がポイントになりますね!
解説を見ているときは「なるほど~」と納得できても、いざ1人で解こうとすると「どこに補助線引くんだっけ(=_=)」となっていまします。
なので、補助線に慣れるための練習問題を用意しました!せっかくなので、このタイミングで完璧に理解しておきましょう^^
共通接線の練習問題
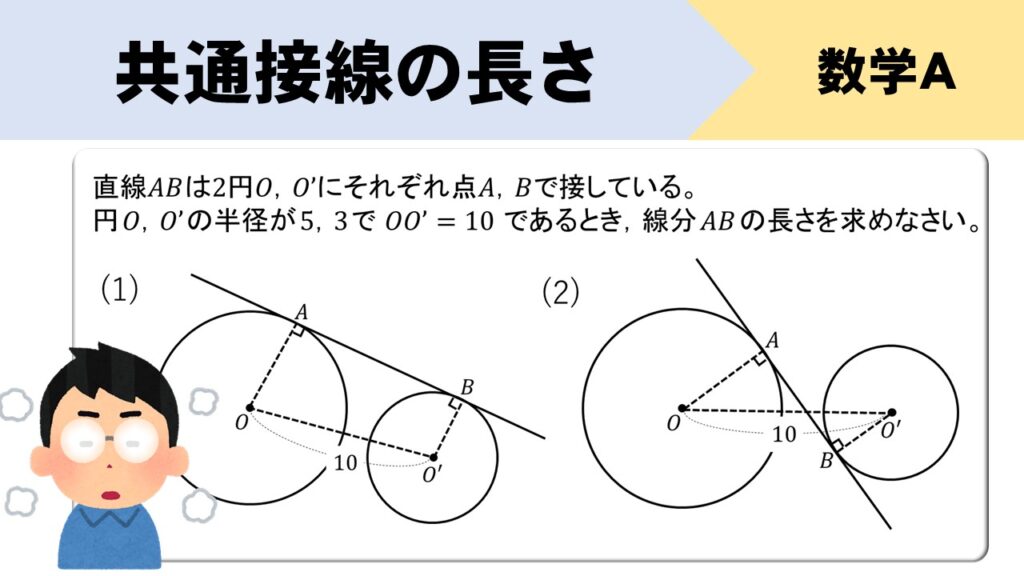
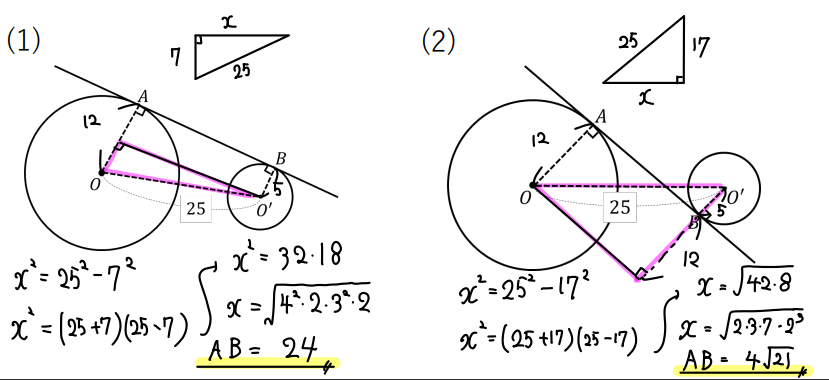
【練習問題】共通接線
直線ABは2円O、O’にそれぞれ点A、Bで接している。円O、O’の半径が12、5で\(OO’=25\)であるとき、線分ABの長さを求めなさい。
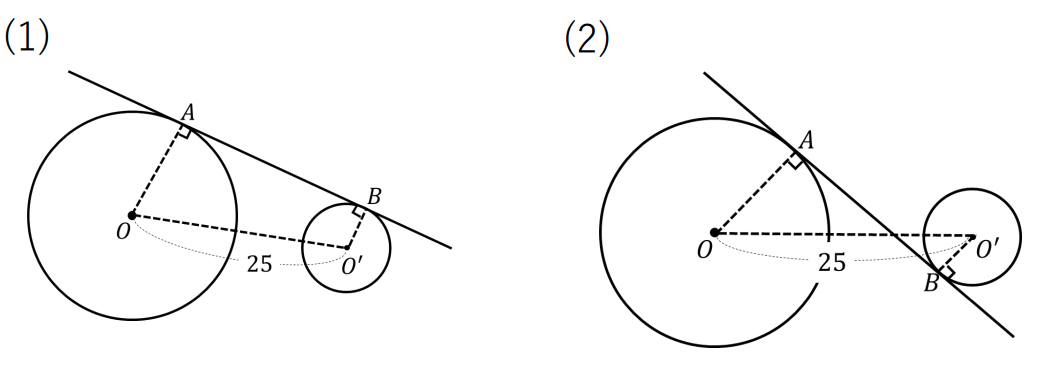
お疲れ様でした!
練習問題はバッチリでしたか?テストに出やすい問題なので、学校ワークなどを通してしっかりと理解を深めておいてくださいね。
では、今回は以上!












コメントを残す