こんにちは!数スタの小田です。
今回は高校数学Ⅱで学習する図形と方程式の単元から「放物線が直線から切り取る線分の長さ」についてイチから解説します。
取り上げる問題はこちら!
【問題①】
放物線 \(y=x^2\) と直線 \(y=x+1\) の交点をA,Bとするとき、線分ABの長さを求めなさい。
【問題②】
直線 \(y=x+k\) が放物線 \(y=x^2\) によって切りとられる線分の長さが3であるとき、定数 \(k\) の値を求めなさい。
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
問題①の解説
【問題①】
放物線 \(y=x^2\) と直線 \(y=x+1\) の交点をA,Bとするとき、線分ABの長さを求めなさい。
線分の長さを求めるためには、
2点A、Bの座標を求めてやろう!
というのがシンプルな流れだと思います。
ですが…実際に座標を求めようとすると…
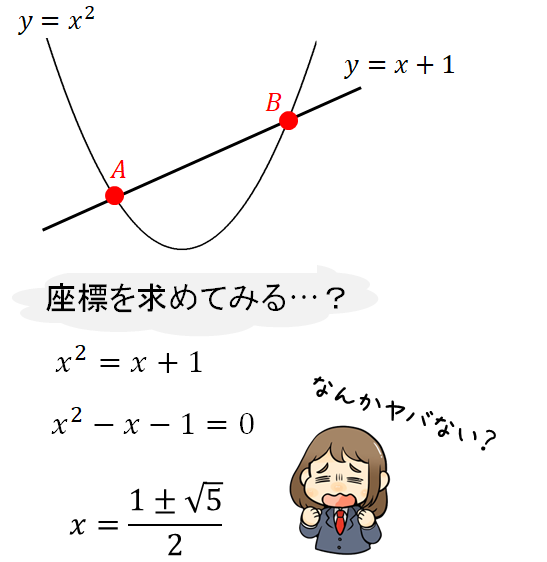
このように複雑な値が出てきてしまい、ここから長さを求めるには計算がハードモードになってしまいます(^^;)
そこで!
いったん、交点のx座標をそれぞれ \(α, β\) と文字でおいて考えることにします。
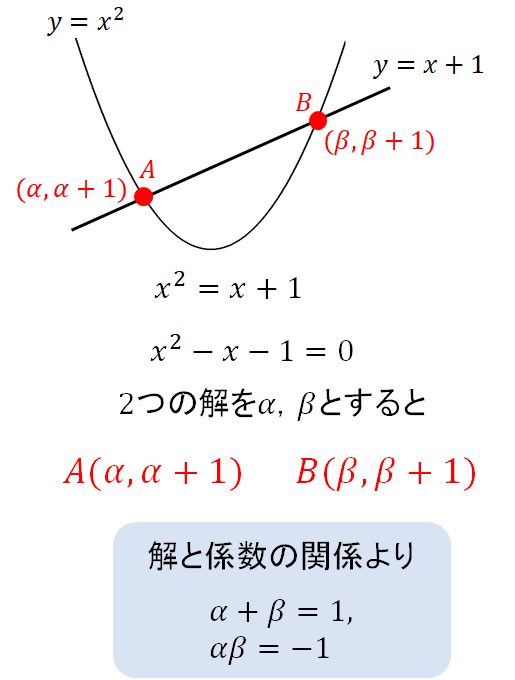
そうすることで、A、Bの座標をシンプルな形で表することができました。
(同時に解と係数の関係から\(α、β\)に関する式をつくっておいてください。あとで使います!)
では、こららの座標を使ってABの長さを表してみましょう。

2乗がでてくると展開したくなりますが、ここはグッと我慢して上のようにまとめていきましょう。
次に \((β-α)^2\) の値を求めます。
ここで使われるのが先ほど準備しておいた「解と係数の関係」の式ですね!
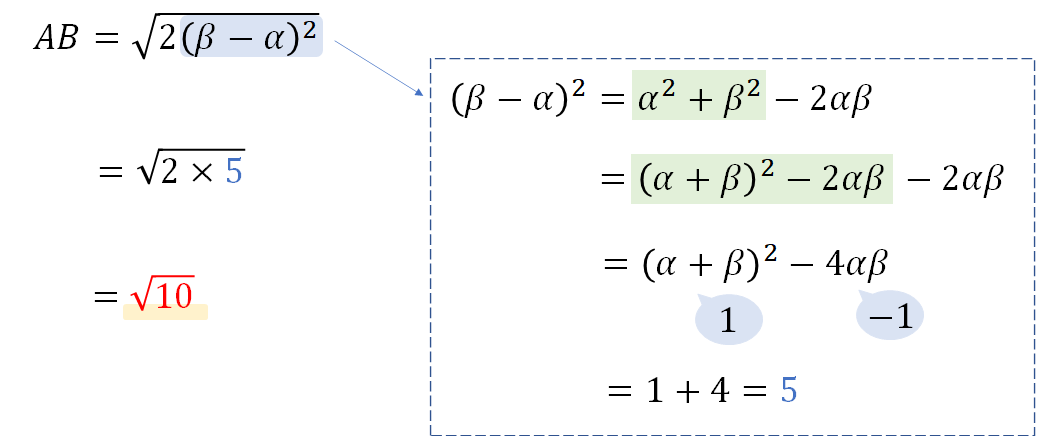
答え
$$AB=\sqrt{10}$$
解き方の流れは理解していただけましたか??
途中で分からなくなった方は、動画解説を見ていただければスムーズに理解できると思います^^
問題②の解説
【問題②】
直線 \(y=x+k\) が放物線 \(y=x^2\) によって切りとられる線分の長さが3であるとき、定数 \(k\) の値を求めなさい。
線分の長さが3になるためには、そもそも直線と放物線との共有点が2個存在していないといけません!
といわけで、まずは前提条件となる\(k\)の範囲を次のように求めておきましょう。
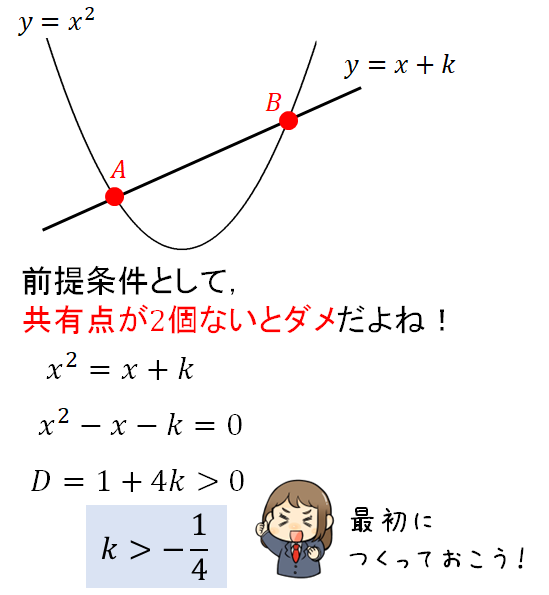
その上で、問題①でもやったように交点の\(x\)座標を文字でおいて長さを表していきましょう。
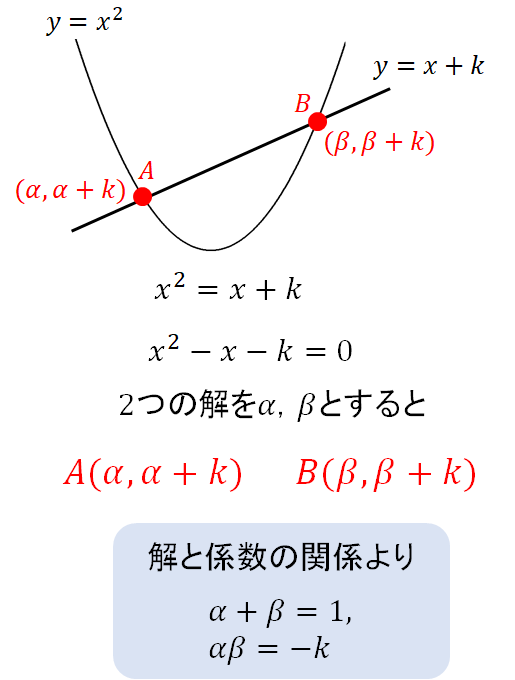
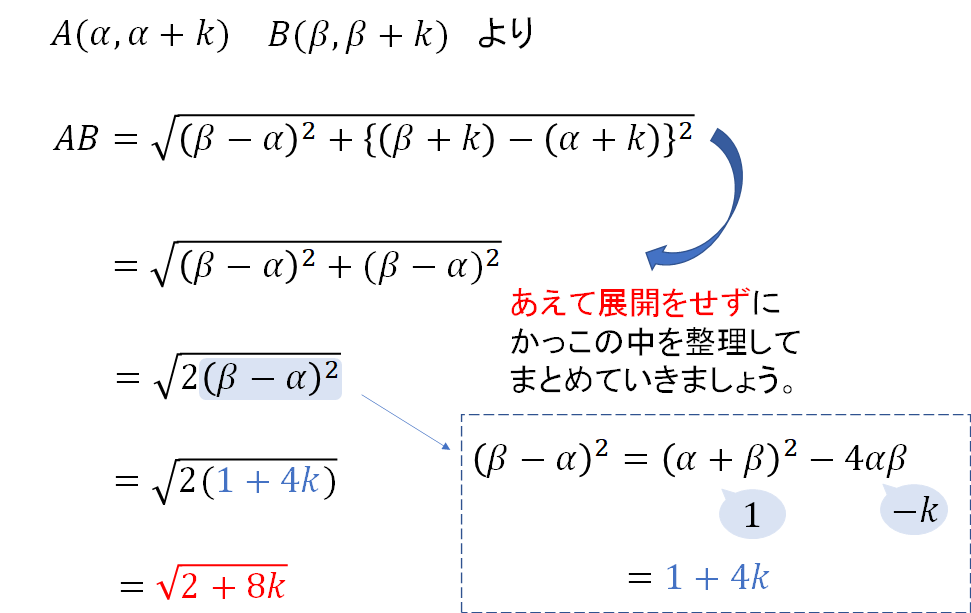
これでABの長さが \(\sqrt{2+8k}\) と表せましたね!
今回の問題ではABの長さが3になると与えられているので、ここから方程式をつくって\(k\)の値を求めます。
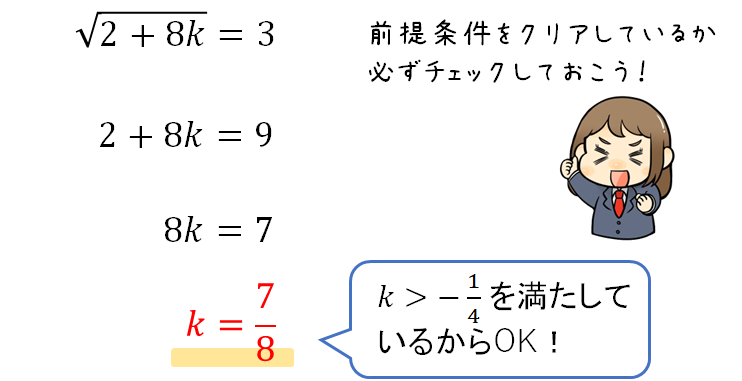
答え
$$k=\frac{7}{8}$$
まとめ
お疲れ様でした!
今回の問題はちょっと難易度が高かったので、最後まで理解するのは大変だった思います。
だけど、よくがんばりましたね^^
「座標を文字で置く ⇒ 解と係数の関係」
この流れは応用問題でよく使われるパターンになってくるので、ぜひ覚えておいてくださいね!
では、今回は以上!

















コメントを残す