こんにちは！数スタの小田です。
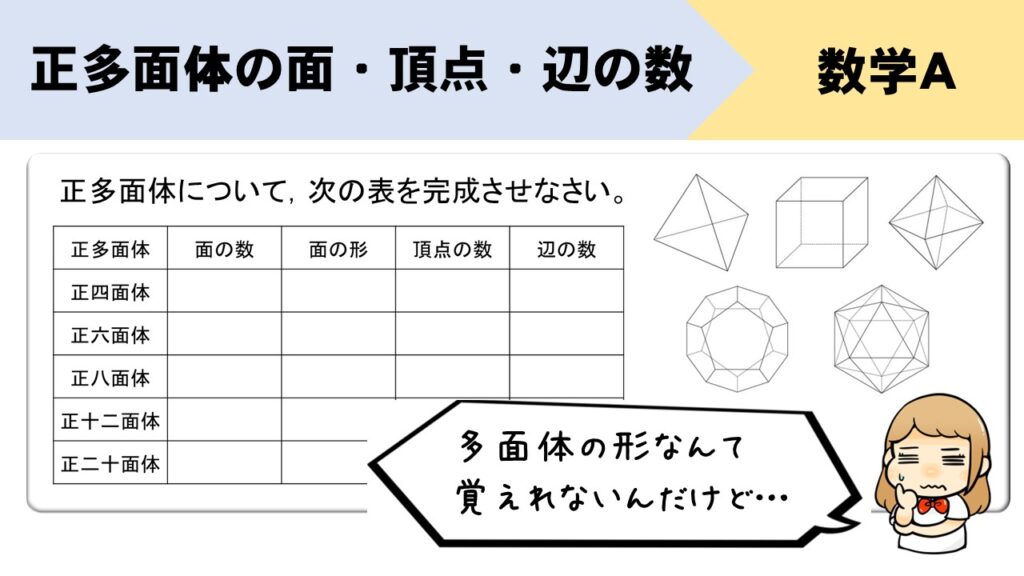
今回は高校数学Aで学習する図形の単元から「正多面体の表の埋め方」について取り上げます。
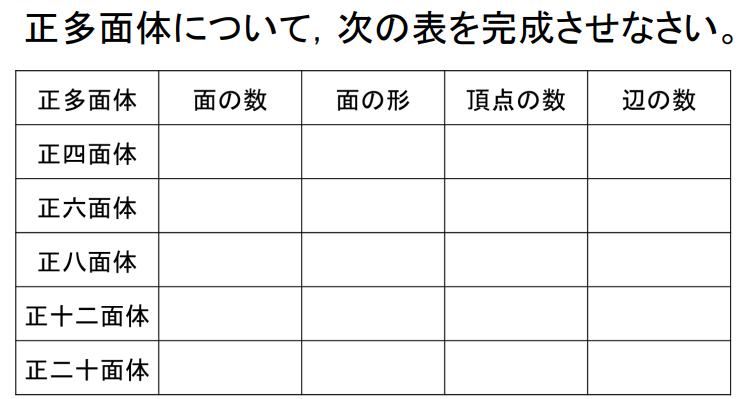
え、これを全部丸暗記しないとダメなの…！？めっちゃキツイんだけど…(-_-)
と、感じている方に向けて、今回の記事では最低限の暗記だけで表をサクッと完成させる方法を紹介します！
サクッと理解したい方は、こちらの動画も参考にしてください！
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします＾＾
正多面体の表を埋めるためのポイント
表を埋めるために最低限、覚えておかないといけない知識があります。
それが「面の形」「オイラーの多面体定理」です。
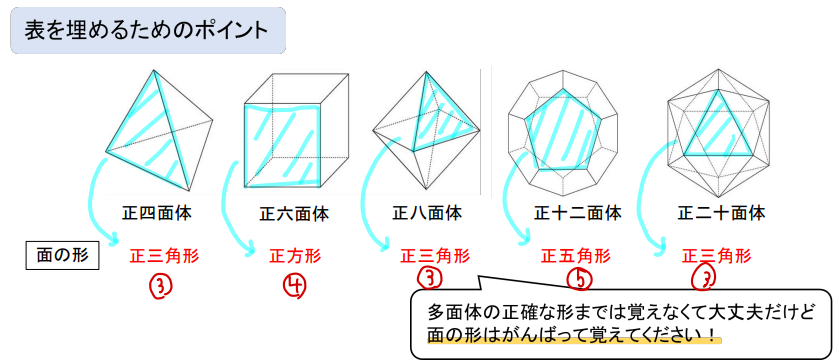
まずはそれぞれの正多面体の面の形を覚えましょう！
順に「正三角形③」「正方形④」「正三角形③」「正五角形⑤」「正三角形③」と変化しています。
3⇒4⇒3⇒5⇒3 と数字の並びで覚えておけば、かんたんに暗記できると思います＾＾
それぞれの正多面体の形を覚えるのは大変ですが、面の形がどうなっているかだけ覚えておけば大丈夫です。
次にオイラーの多面体定理を覚えておきましょう！
これは「頂点の数」「辺の数」「面の数」の関係性を表したものですが、他の問題でも活用することがあるので、これをキッカケにしっかりと覚えるように。
正多面体の表の埋め方
正多面体の表は以下の順に埋めていくとスムーズです！
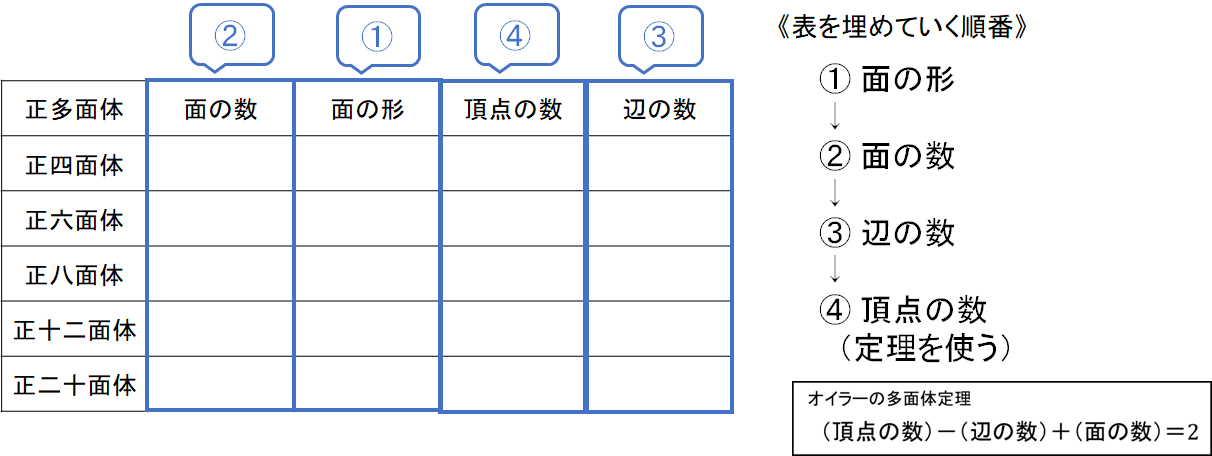
STEP1 面の形
まずは面の形を埋めましょう。
ここは先ほどのポイントでお伝えしたように「暗記」で対処する部分になります。
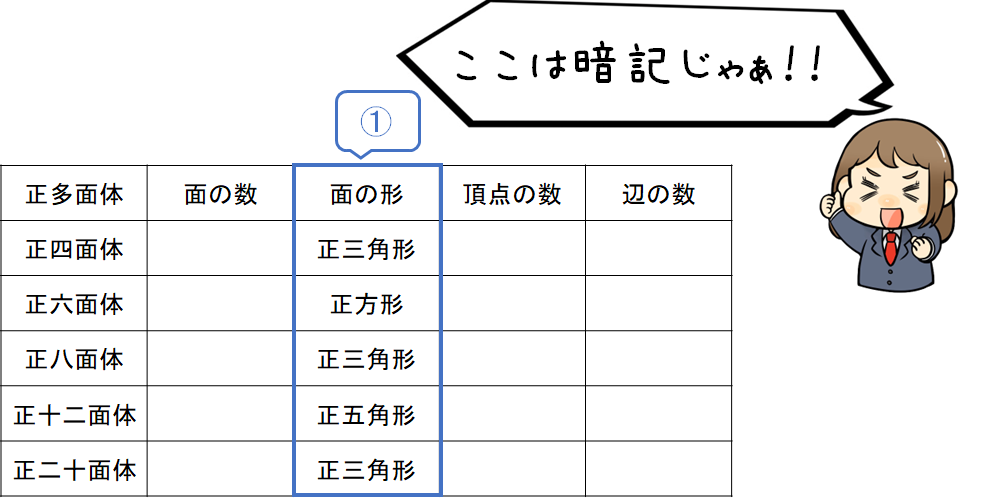
上から順に 3⇒4⇒3⇒5⇒3 ですね！
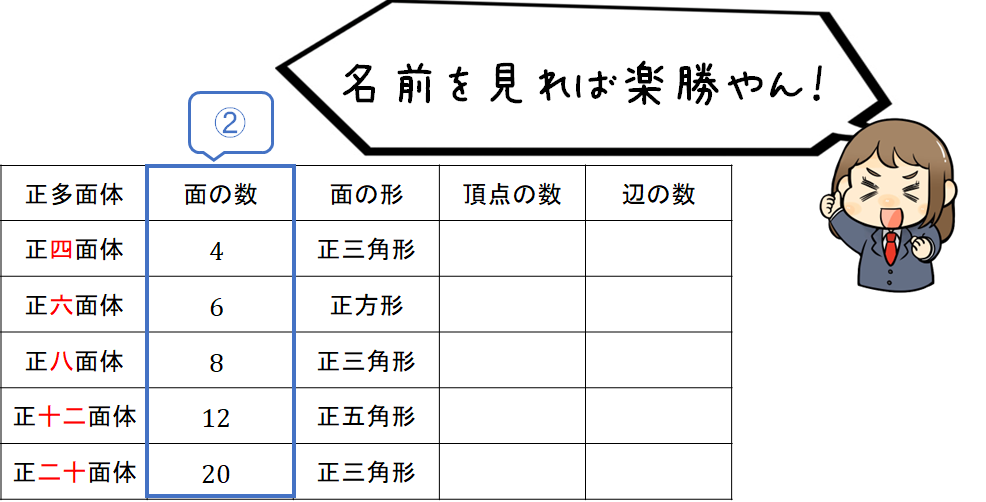
STEP2 面の数
続いて面の数を埋めましょう。
これは正多面体の名前を見れば楽勝です！
正四面体 ⇒ 4つの面がある
正六面体 ⇒ 6つの面がある
このように名前に面の数が書いてあるので、すぐに表を埋めることができますね＾＾
STEP3 辺の数
次は辺の数を求めます。ここから少しだけ計算を活用していきます。
正四面体を例にして辺の数え方を確認してみましょう。
正四面体は「正三角形 4面」によってつくられています。
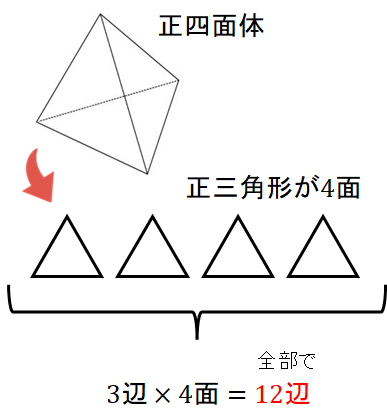
パーツを並べてみると、正三角形には3辺、それらが4面。
つまり、組み立てる前のパーツ時点では全部で3×4＝12辺あります。
これらを組み合わせて正四面体を作ると、2つの辺がくっついて1つの辺になっていることがわかりますね。
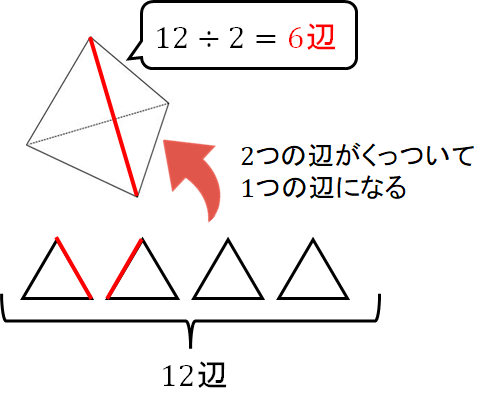
ということは、パーツ時点では12辺あったものが、組み合わせて正四面体を作ったところ、辺の数が半分の6辺になります。
このように「パーツの辺の合計を求めて、それを半分にする」という手順で求めていきます。
長々と説明を書いたので、ちょっと難しく思われたかもしれませんが、表のこの部分を見ながら計算していけばラクにできますよ＾＾
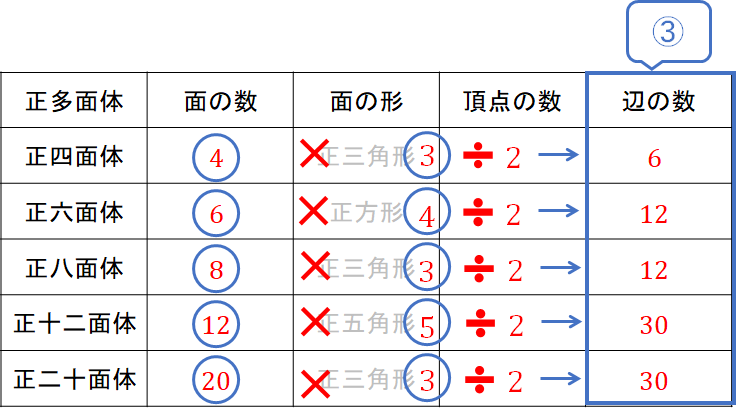
※ 表にある×はかけ算を表しています。
STEP4 頂点の数（定理を使う）
最後に頂点の数を埋めます。
ここではすでに埋めている「面の数」「辺の数」をオイラーの多面体定理に当てはめて計算します。
例えば、正四面体の頂点の数は次のように求めることができます。
他も同様にして求めると、次のように表を完成させることができますね！
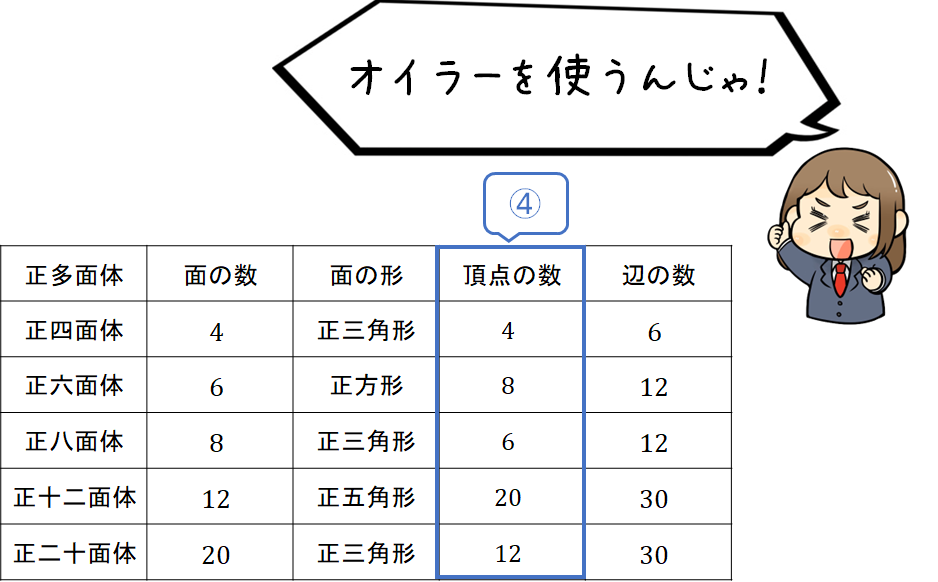
というわけで、これで表は完成です！
「面の形」「オイラーの多面体定理」
この2つについては覚えてもらう必要がありますが、わざわざ丸暗記しなくても、たったコレだけでサクッと表が埋められるようになるので、だいぶ気がラクになりますよね＾＾
慣れるまでに練習は必要だと思いますが、今回の記事を参考にしながら表の埋め方を覚えてもらえると嬉しいです！
それでは、今回は以上！
最後までお疲れ様でした＾＾
コメントを残す