高校数学Aで学習する整数の性質の単元から
「最大公約数、最小公倍数の求め方、性質」
についてまとめていきます。
この記事を通して、
- 最大公約数、最小公倍数、互いに素とは何か
- 素因数分解を使った最大公約数、最小公倍数の求め方
- 逆割り算を用いた求め方
- 最大公約数、最小公倍数の性質 \((ab=gl)\) など
今回の内容はこちらの動画でも解説しています!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
最大公約数、最小公倍数、互いに素とは?
最大公約数
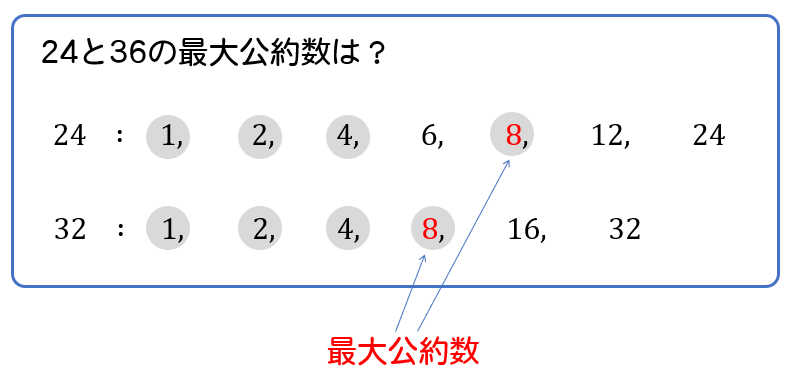
2つ以上の整数について、共通する約数をこれらの公約数といい、公約数のうち最大のものを最大公約数といいます。
公約数は最大公約数の約数になっています。
以下の例では、公約数 \(1,2,34,8\) はすべて最大公約数 \(8\) の約数になっていますね。
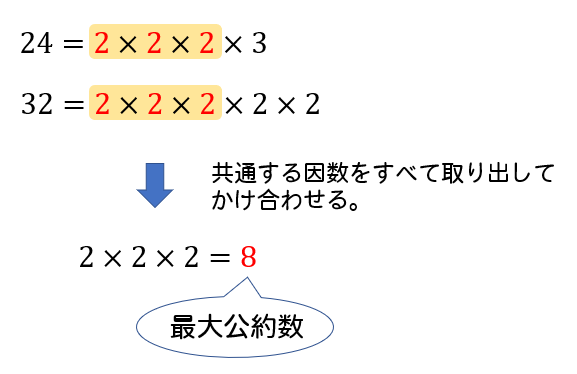
また、最大公約数は、それぞれに共通する因数をすべて取り出して掛け合わせた数になります。
最小公倍数
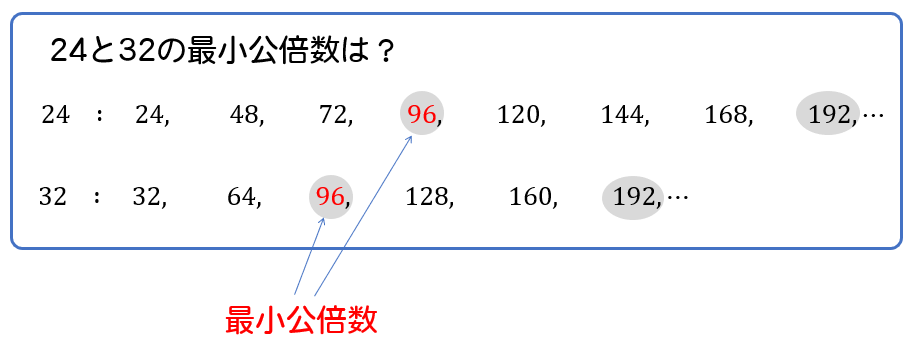
2つ以上の整数について、共通する倍数をこれらの公倍数といい、正の公倍数のうち最小のものを最小公倍数といいます。
公倍数は最小公倍数の倍数になります。
以下の例では、公倍数 \(96,192,288, \cdots \) はすべて最小公倍数 \(96\) の倍数になっていますね。
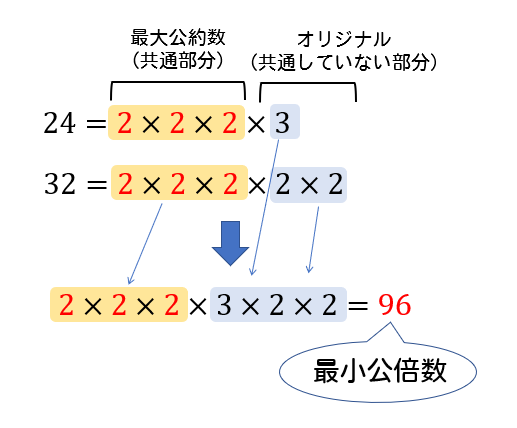
また、最小公倍数は、最大公約数(共通部分)にそれぞれのオリジナル部分(共通していない部分)を掛け合わせた値になっています。
互いに素
2つの整数の最大公約数が1であるとき,これらの整数は互いに素であるといいます。
\(3\) と \(5\) は最大公約数が \(1\) だから、互いに素。
\(13\) と \(20\) は最大公約数が \(1\) だから、互いに素。
これ以上、約分ができない数どうしは「互いに素」っていうイメージだね!
また、互いに素である数には次のような性質があります。
【互いに素の性質】
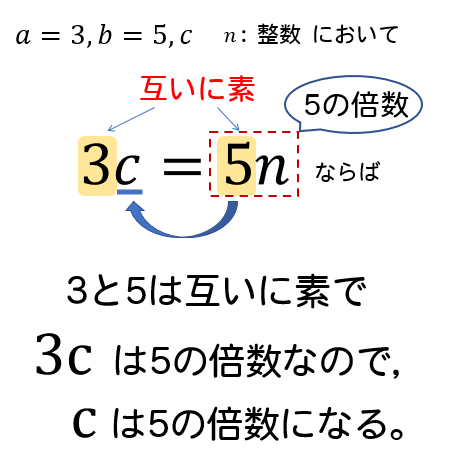
\(a, \ b, \ c\) は整数で、\(a\) と \(b\) が互いに素であるとする。このとき
- \(ac\) が \(b\) の倍数であるとき,\(c\) は \(b\) の倍数
- \(a\) の倍数であり,\(b\) の倍数でもある整数は,\(ab\) の倍数
この性質は、のちに学習する不定方程式のところで活用することになります。
次のようなイメージで覚えておいてくださいね!
素因数分解を使って最大公約数、最小公倍数を求める
【問題】
次の2つの整数の最大公約数と最小公倍数を求めよ。
(1)\(60, \ 72\)
(2)\(360, \ 588, \ 756\)
素因数分解を活用して、これらの最大公約数、最小公倍数を求めてみましょう。
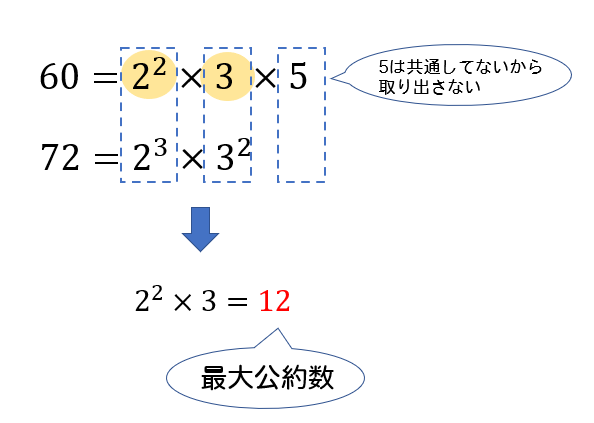
(1)\(60, \ 72\) をそれぞれ素因数分解をします。
最大公約数とは、それぞれの共通する素因数をすべて取り出して掛け合わせた数。
なので、素因数分解した式を書き並べて、共通する素因数の個数が最も小さいものを取り出せばOKです。
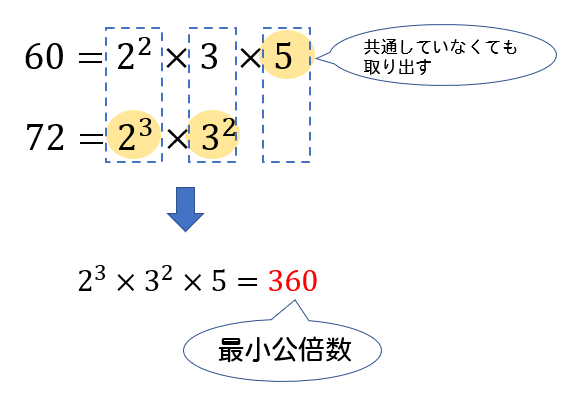
最小公倍数は、最大公約数とそれぞれのオリジナル因数を取り出して掛け合わせた値になります。
なので、素因数分解をした式を書き並べ、それぞれの因数の個数が大きいものを取り出していけばOKです。
答え
(1)最大公約数 \(12\) , 最小公倍数 \(360\)
次に(2)3つの数についても考えてみましょう。
ただ、3つになっていても考え方は同じ事です。
それぞれの数を素因数分解して、ルールに従って因数を取り出していきましょう。

答え
(2)最大公約数 \(12\) , 最小公倍数 \(52920\)
逆割り算を用いて最大公約数、最小公倍数を求める
【問題】
次の2つの整数の最大公約数と最小公倍数を求めよ。
(1)\(60, \ 72\)
(2)\(360, \ 588, \ 756\)
次は逆割り算を用いて、最大公約数、最小公倍数を求める方法を紹介します。
こちらのやり方は、小学校で習ったという方もいるかもしれませんね。
それくらい簡単なやり方なので、サクッと身につけておきましょう。
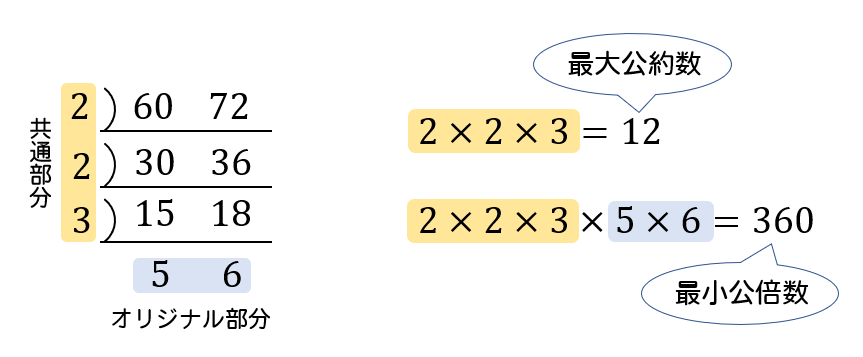
それぞれを割り切ることができる素数で、どんどん割っていきます。
これ以上、割れないところまで計算し、左に出てきた素数を掛け合わせたものが最大公約数。
左に出てきた素数と割ることができずに残った部分をすべて掛け合わせたものが最小公倍数となります。
3つの数について逆割り算を用いる場合
まずは、3つの数を割り切ることができる素数で割っていきます。
これ以上割れないところまできたら、次は2つの数を割り切ることができる素数を見つけ割っていきます。このとき、割り切ることができない数はそのままにしておきます。
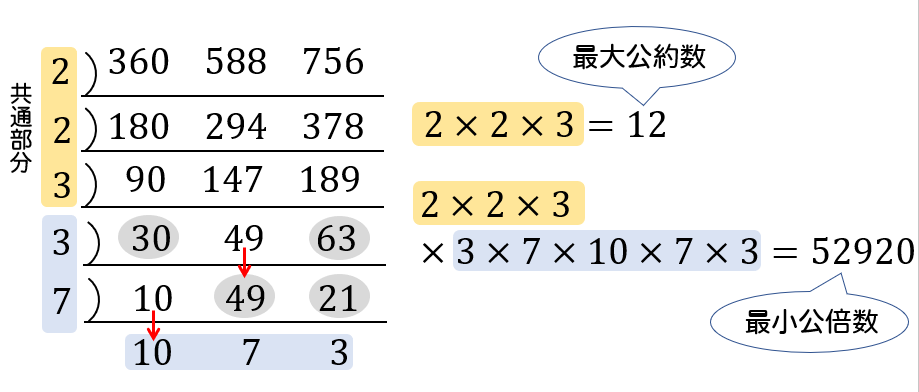
3つの数を割り切ることができた素数をすべて取り出してかけたものが最大公約数。
左に出てきた数と残った数をすべてかけ合わせたものが最小公倍数となります。
最大公約数、最小公倍数の性質
最大公約数と最小公倍数には次のような性質があります。
【最大公約数と最小公倍数の性質】
2つの正の整数 \(a, \ b\) の最大公約数を \(g\), 最小公倍数を \(l\) とする。
- \(a=a’g\), \(b=b’g\) (\(a’\) と \(b’\) は互いに素な自然数)
- \(l=a’b’g\)
- \(gl=ab\)
ただ、これらの性質って式で見てるだけではイメージがつかみにくいよね(^^;)
なので、冒頭で具体例としてあげた \(24\) と \(36\) の最大公約数、最小公倍数で上の性質を確認してみましょう。
まず①の性質について
それぞれの数は最大公約数(共通部分)とオリジナル部分(共通していない部分)に分けることができますよっていう意味ですね。そして、オリジナル部分は必ず互いに素になっています。

次に②の性質について
これは、最小公倍数は最大公約数(共通部分)とそれぞれのオリジナル部分をかけた値になりますよって意味ですね。
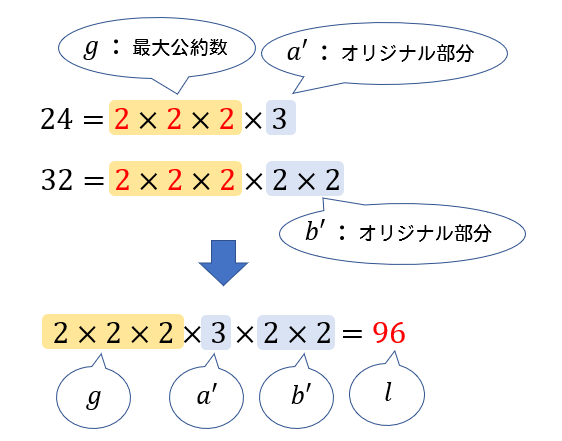
最後に③の性質について
それぞれの数をかけると、最小公倍数と最大公約数をかけた値と等しくなるって意味ですね。
実際にそれぞれの数をかけてみて、パーツを組み替えてみると納得できると思います。
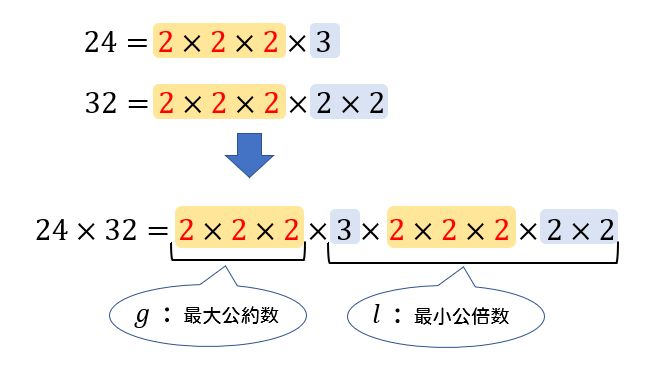
では、これらの性質を用いた例題を紹介しておきます。
【例題】
最大公約数が \(15\),最小公倍数が \(180\) である2つの自然数 \(a, b\) の組をすべて求めよ。ただし,\(a<b\) とする。
最大公約数が \(15\) であることから、互いに素である自然数 \(a’, \ b’ \) を用いて、
\(a=15a’, \ b=15b’\) と表すことができます。
次に、\(l=a’b’g\) を用いると、
$$\begin{eqnarray}180&=&15a’b’\\[5pt]a’b’&=&12 \end{eqnarray}$$
となります。
\(a’, \ b’\) は互いに素である自然数であり、\(a<b\) であることから
その組み合わせは、\((a’,b’)=(1,12), \ (3,4)\) の2組となります。
よって、\((a,b)=(15, \ 180), \ (45,60)\)
答え
$$(a,b)=(15, \ 180), \ (45,60)$$
まとめ
お疲れさまでした!
最大公約数、最小公倍数の求め方、性質については理解してもらえましたか??
記事の最初に説明した通り、
最大公約数は、それぞれに共通した部分をかけ合わせたもの。

最小公倍数は、最大公約数にそれぞれのオリジナル部分をかけ合わせたもの。

このイメージを持っておければ、最後に紹介した最大公約数と最小公倍数の性質についても理解ができるはずです(^^)
まぁ、何度も練習していれば、考えなくてもスラスラと式が作れるようになります。
というわけで、まずは練習あるのみだ!
ファイトだ(/・ω・)/















3c=5は草
ホントだ、草ですね(^^;)
訂正しておきました!
ご丁寧にありがとうございました。
よくわかりました