今回は高校数学Aで学習する整数の性質の単元から「最小公倍数から\(n\)の値を求める」についてイチから解説します。
取り上げる問題はこちら!
【問題】
\(n\)は正の整数とする。
\(n\)と36の最小公倍数が504であるような\(n\)の値をすべて求めなさい。
記事の最後には練習問題も用意してるので、ぜひ取り組んでみてくださいね!
では、解説に進んでいきましょう(‘ω’)ノ
今回の内容をサクッと理解したい方はこちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
最小公倍数のポイント!
今回の問題を理解するためには「素因数分解を使って最小公倍数を求めるやり方」を思い出す必要があります。
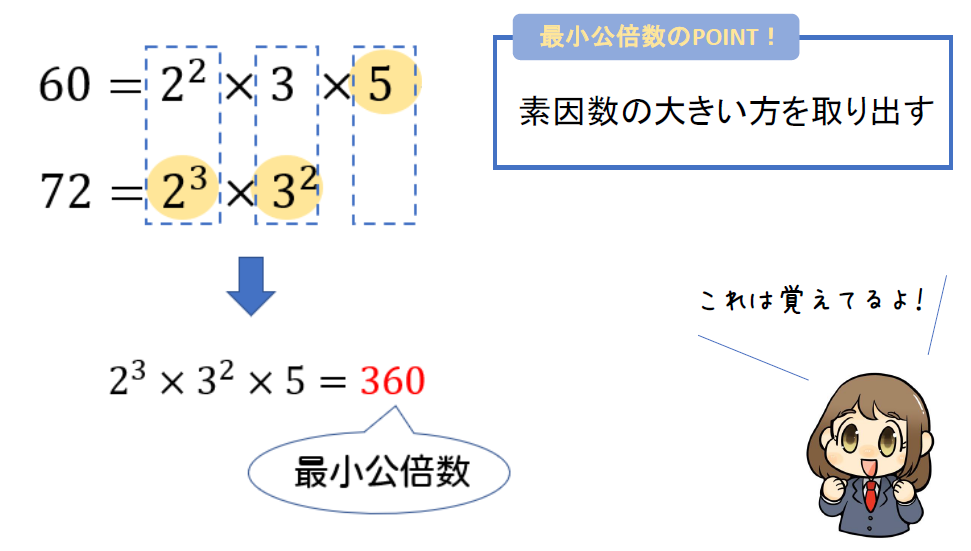
最小公倍数を求めるには、それぞれの数を素因数分解して素因数の大きい方を取り出すというのがやり方でしたね。
これをしっかりと頭に入れた状態で、今回の問題の解説をチェックしていきましょう。
問題の解き方をイチから!
【問題】
\(n\)は正の整数とする。
\(n\)と36の最小公倍数が504であるような\(n\)の値をすべて求めなさい。
この問題を解くためには次のように考えていきます。
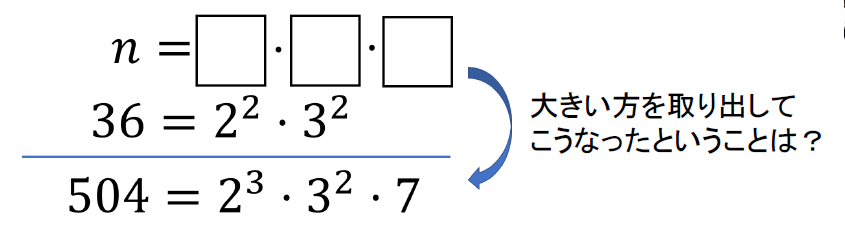
それぞれを素因数分解して、パーツを見比べていきます。
\(n\)と36のパーツを見比べて大きい方を取り出した結果、\(2^3\cdot 3^2\cdot 7\)になったということです。
このことから、\(n\)のパーツを次のように予測することができます。

3のパーツについては、{なし、\(3\)、\(3^2\)}の3パターン考えられますね。
だから、上の画像のように\(n\)の値も3パターン求まります。
どうかな?
仕組みは理解してもらえたかな?
それぞれを素因数分解して、最小公倍数の結果から逆算して\(n\)のパーツを予測するんじゃ!!
ということです(‘ω’)ノ
仕組みが理解できたら、練習問題でチェックしておこう!
演習問題にチャレンジ!
【問題】\(n\)は正の整数とする。
(1)\(n\)と18の最小公倍数が180であるような\(n\)の値をすべて求めなさい。
(2)\(n\)と90の最小公倍数が900であるような\(n\)の値をすべて求めなさい。
まとめ
お疲れ様でした!
今回のポイントは「素因数分解を活用して、逆算して考える」ということでしたね^^
それぞれ数を素因数分解して、同じパーツを並べて書いてみると読み取りやすくなるのでおススメです!



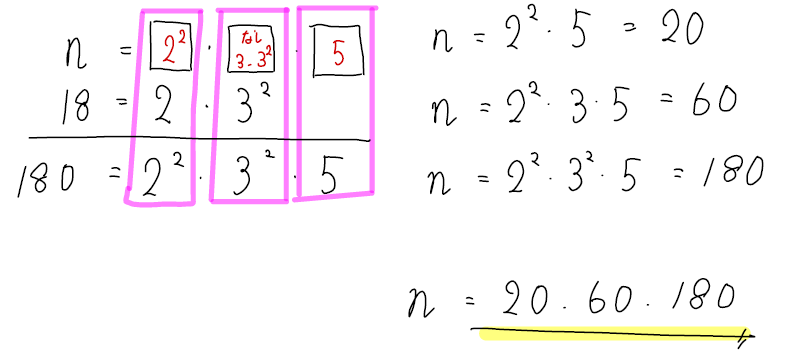
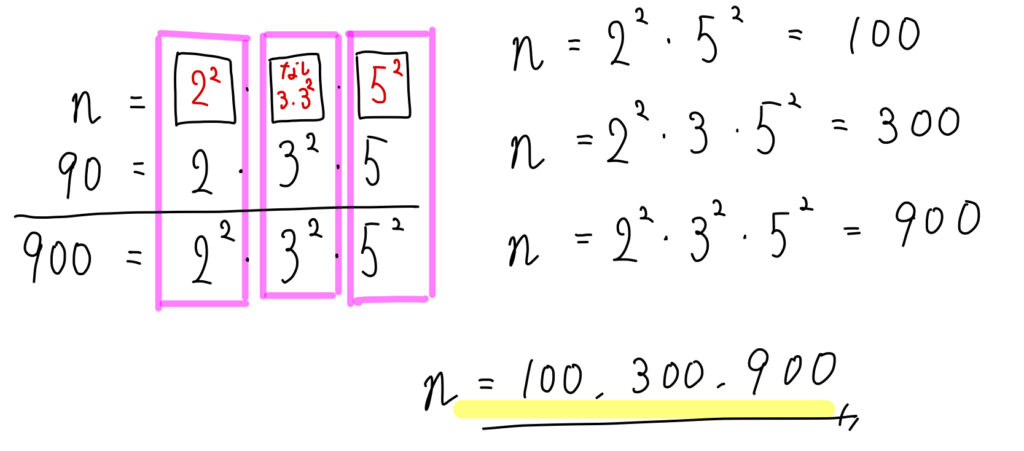











tryでは分からなかったのが、すんなり理解できました。
ありがとう!
お役に立てて嬉しいです!
今後も困ったことがあればぜひ数スタを!
めちゃくちゃわかりやすかったです!ありがとうございます!