こんにちは!数スタの小田です。
今回は高校数学Ⅰで学習する三角比の単元から「円に内接、外接する正\(n\)角形の面積」についてイチから解説します。
取り上げる問題はこちら!
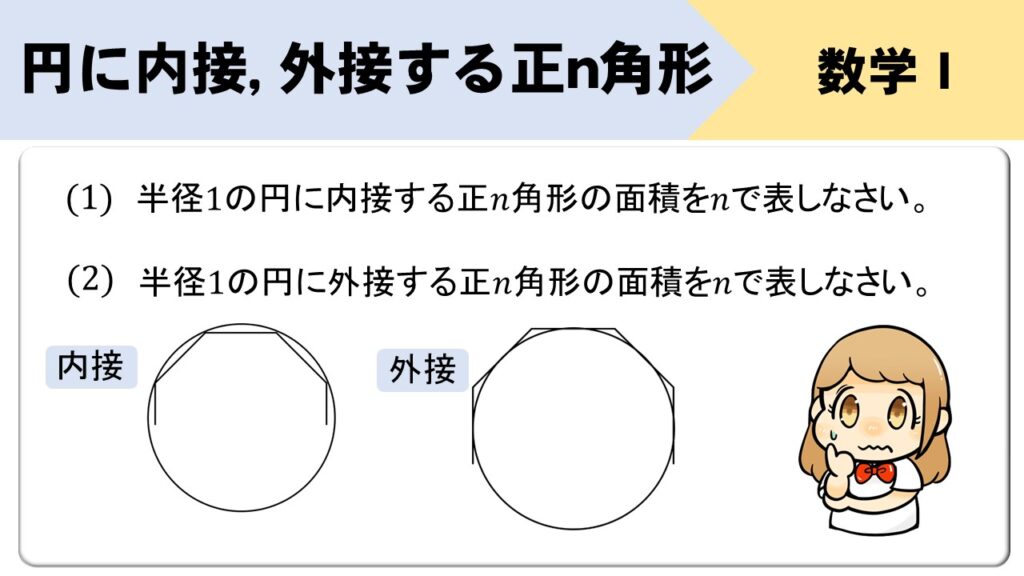
【問題】次の問いに答えなさい。
(1) 半径1の円に内接する正\(n\)角形の面積を\(n\)で表しなさい。
(2) 半径1の円に外接する正\(n\)角形の面積を\(n\)で表しなさい。
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
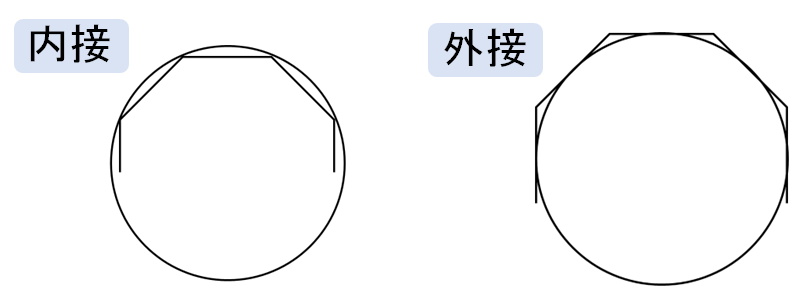
円に内接する正n角形
正\(n\)角形の面積を一発で求めるのは難しいので、\(n\)分割された三角形を考えます。
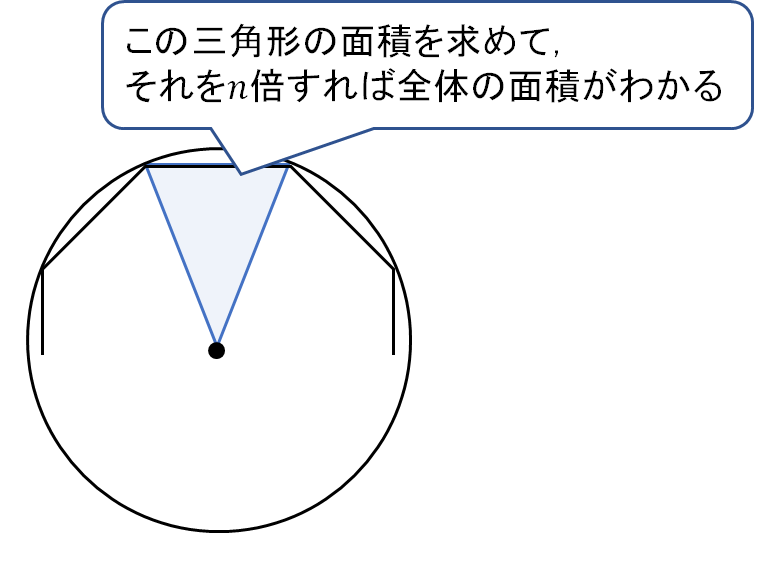
では、この三角形の辺、角の大きさを書き込んでみましょう。
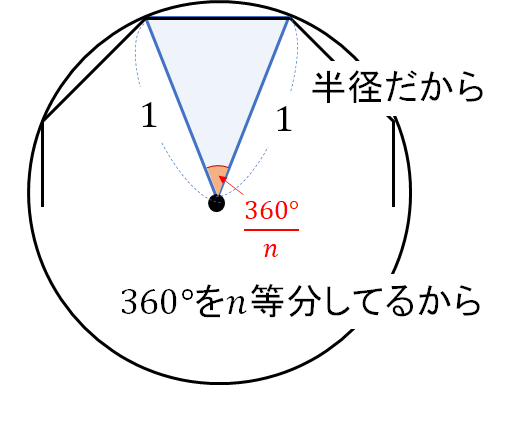
すると、こんな感じですね!
あとは、三角比の面積公式に当てはめてやればOKです。
【面積公式】
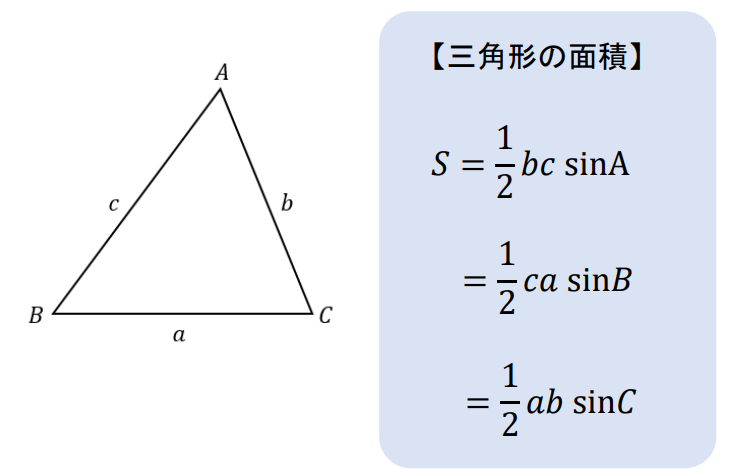
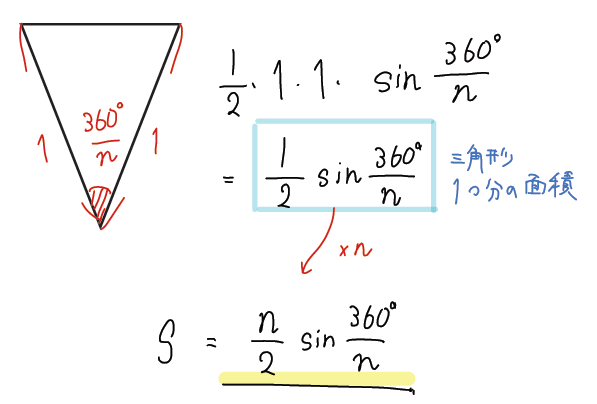
三角形の面積が求まったら、それを\(n\)倍してやれば正\(n\)角形の面積が求まりますね!
円に外接する正n角形
外接する場合も先ほどと同じように、\(n\)等分された三角形を考えていくのですが…
長さに注意が必要です!
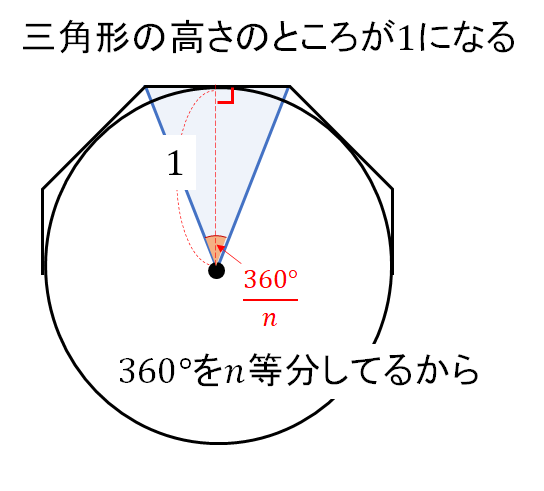
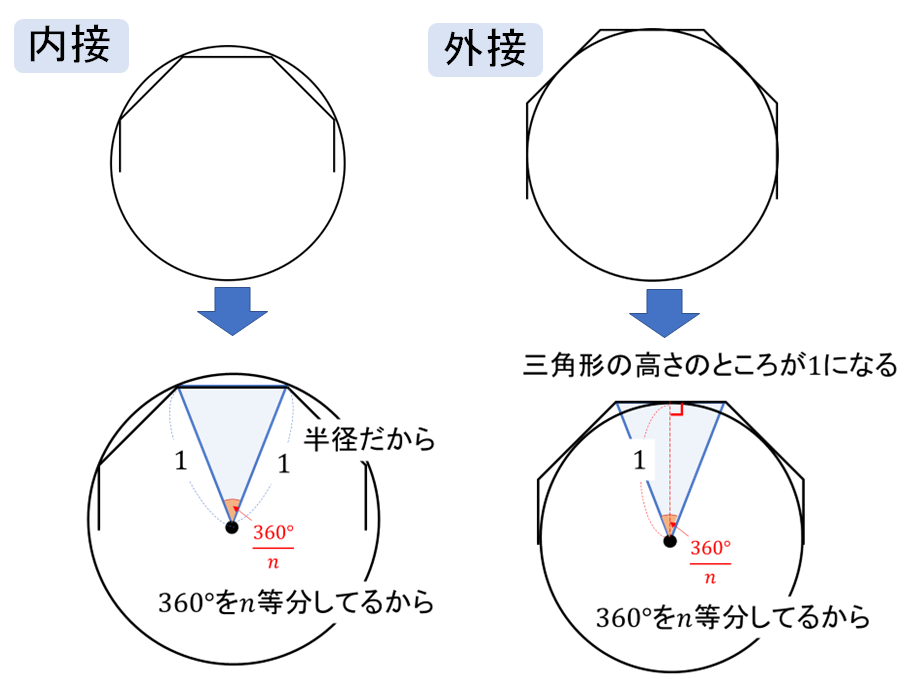
このように、円の半径からは「三角形の高さが1になる」ということしか読み取れません。
斜めの長さがわからない状態では、面積公式が使えないので困ってしまいます…
そこで!次の直角三角形に注目しましょう!
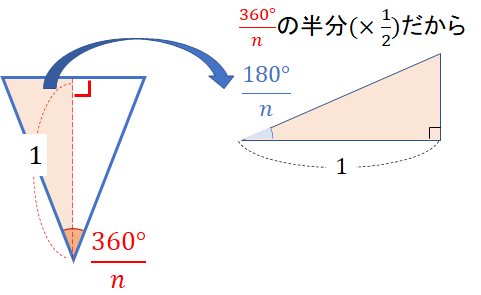
そうすることによって、次のように三角形の底辺を求めることができます。
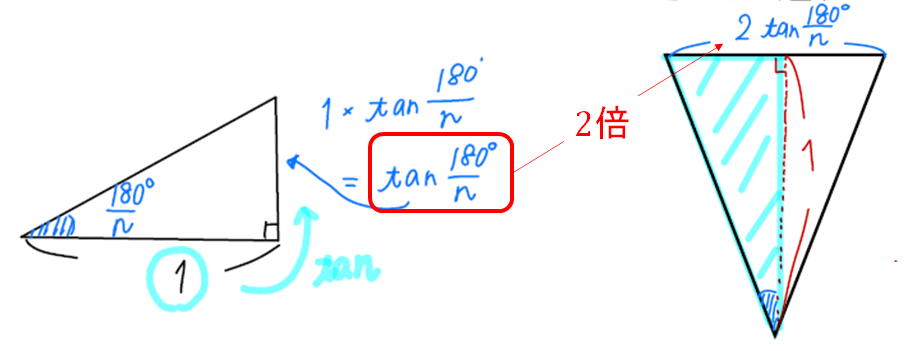
(この辺がわかりづらい場合は、記事の冒頭にある動画を参考にしてください!)
これで三角形の底辺、高さが揃ったので面積を求めることができますね^^

あとはこれを\(n\)倍すれば、正\(n\)角形の面積が求まります!
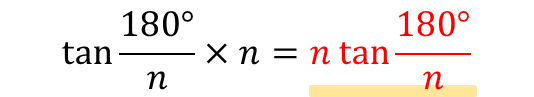
まとめ
お疲れ様でした!!
それぞれ自力で思いつくのは難しいかもしれませんが、一度解いたことがあれば楽勝で対応できるようになると思います^^
ポイントとしては、
「半径が三角形のどの部分になるか」「中心角の表し方はどうか」
この2点をおさえておけばOKです!
しっかりと覚えておいてくださいね^^
では、今回は以上!














すみません!
円に外接する正n角形の所の図が間違って居ます。
でも解説は凄く分かり易かったです。
ご指摘ありがとうございます!!
めっちゃ変なミスしてましたね(^^;)
訂正しておきました!
すごく分かりやすかったです!参考にした本などあれば教えていただきたいです
ありがとうございます!
青チャート、ニューアクション、教科書準拠のワークなどを参考にしています!