今回は高校数学Ⅰで学習する三角比の単元から
「直角三角形の辺の長さを求める方法」についてイチから解説していきます！
今回取り上げるのはこちらの3題です。
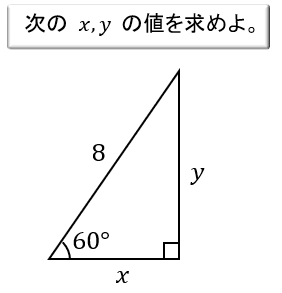
（1）
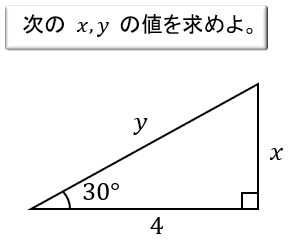
（2）
（3）
動画でサクッと理解したい方は、こちらをどうぞ！
絶対覚える！三角比と辺の長さの関係
三角比と直角三角形の辺の長さにはこのような関係があります。
斜辺に\(\cos\)をかけると底辺
斜辺に\(\sin\)をかけると高さ
底辺に\(\tan\)をかけると高さ
このように、ある1辺の長さと三角比の値を利用して、他の辺の長さを求めることができます。
（この計算は、物理の学習でよく活用します）
なぜこのように求めることができるのか、詳しく学びたい方は冒頭の動画講義をチェックしてみてね！
では、それぞれの問題の解き方について確認してみましょう。
（1）の解説
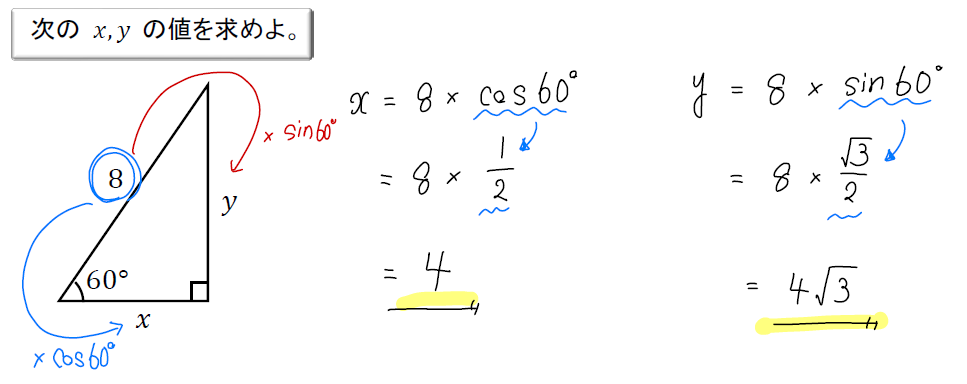
\(x\)（底辺）を求めるには、斜辺に\(\cos\)をかける。
\(y\)（高さ）を求めるには、斜辺に\(\sin\)をかける。
これを計算していけばバッチリ求めることができますね( ｀ー´)ノ
（2）の解説
今回は斜辺の長さが分かっていないので、
\(x\)（高さ）を求めるには、底辺に\(\tan\)をかけて求めましょう！
次に、斜辺の\(y\)を求めるためには、
ちょっとややこしい式になりますが、斜辺と底辺の関係性から式を作りましょう。
斜辺 \(y\) に\(\cos\)をかけると底辺4になるので、
$$y\times \cos{30°}=4 $$
という方程式を作って解いてください。
（3）の解説
角の大きさがキリの悪い値になっていますが、やることは同じです！
問題文に与えられている\(\tan\)の値を活用して計算していけばOKです。
\(x\)（高さ）を求めるには、底辺に\(\tan\)をかける。
これで計算していきましょう！
まとめ！
お疲れさまでした！
これで三角比を利用して、辺の長さを求める問題はバッチリのはず(‘◇’)ゞ
今後もいろんな場面で活用していくようになるので、三角比と辺の長さの関係についてはしっかりと覚えておいてくださいね。
今回の知識を活用した実用的な問題も用意しています！
これができるようになればテストもバッチリ＾＾
ぜひ挑戦してみてくださいね！
コメントを残す