中線定理とは何!?
ということで、まず中線定理を紹介しておきます。
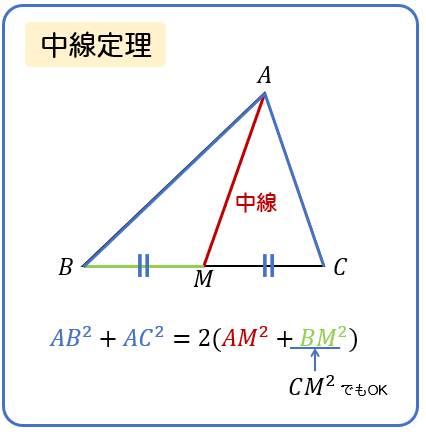
このように、三角形に中線が引かれたときに使える定理です。
中線定理って、どこの辺を見ればいいのか覚えられない…
という方は、次のようなイメージを持っておくといいですよ!
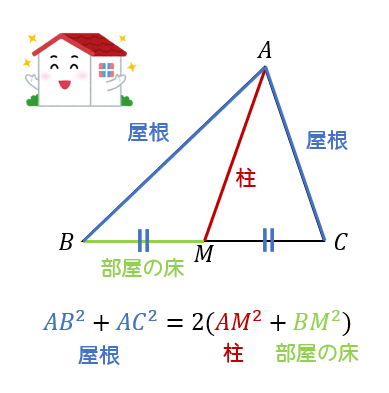
三角形を家に見立てて「屋根」「柱」「部屋の床」として考えてみてください。
そして、「屋根の2乗の和は、柱と部屋の床の2乗の和を2倍したものと等しい。」
とイメージしておくと、
あれ?どこの辺を見ればいいんだっけ?
というド忘れを防ぐことができるようになります(^^)
私は式で覚えるのがニガテなので、このようなイメージで中線定理を覚えています。
そして、この定理は次のように中線の長さを求めるときに用いられます。
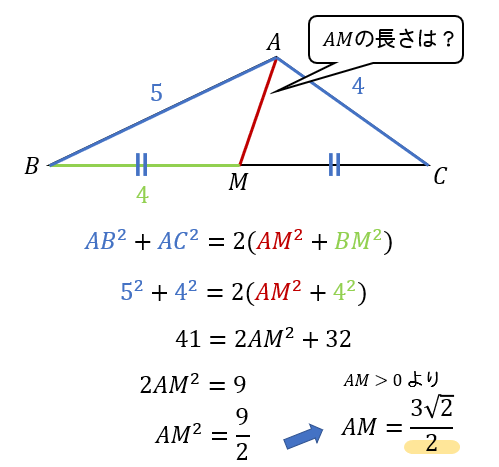
では、そんな中線定理なのですが、
なぜこのような定理が成り立つのでしょうか。
様々な証明方法があるのですが、三角比の単元で紹介される定理だということから「余弦定理」を使った証明方法について紹介しておきます。
証明方法を理解した上で、最後に練習問題を用意しているので、
そこで定理を使いこなせるかどうか確認してみてくださいね!
今回の内容はこちらの動画でも解説しています(‘◇’)ゞ
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
【中線定理】余弦定理を使った証明
\(△ABC\) の辺\(BC\) の中点を \(M\) とし,\(∠AMB=\theta\) とする。
\(AB^2+AC^2=2(AM^2+BM^2)\) が成り立つことを証明せよ。
まずは、左辺の\(AB^2\) ,\(AC^2\) をそれぞれ式で表してみましょう。
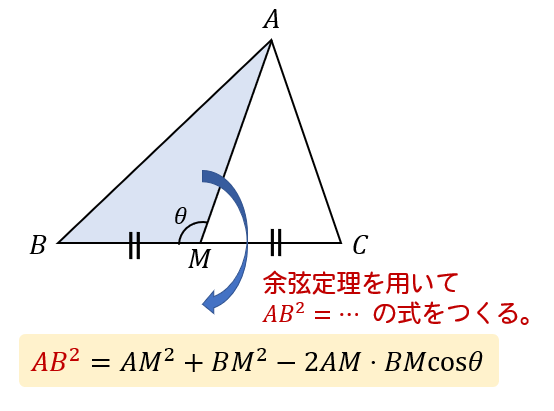
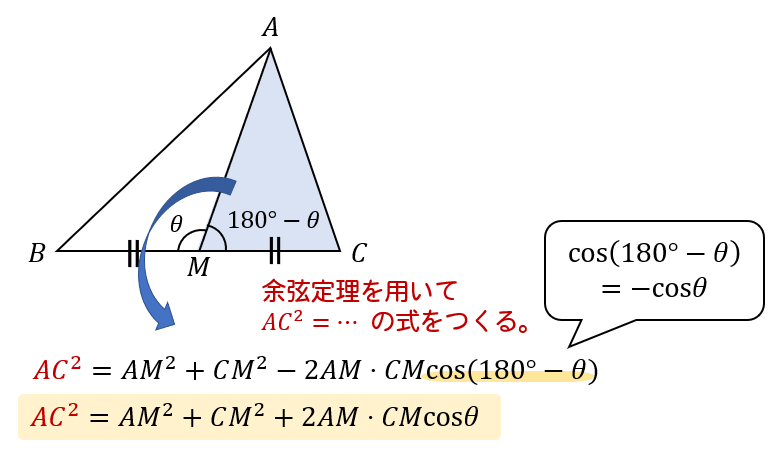
それぞれ式で表すことができたら、
中線定理の左辺、\(AB^2+AC^2\) に代入してみましょう。
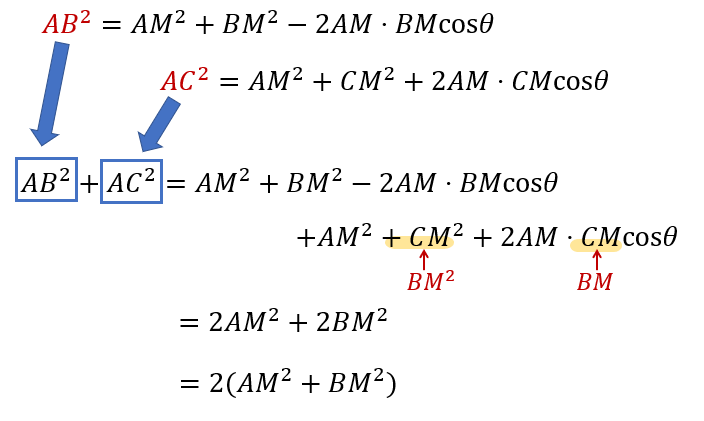
以上より
\(AB^2+AC^2=2(AM^2+BM^2)\) が成り立つことが証明できました!
余弦定理を使ったら簡単に証明ができますね(^^)
【中線定理】練習問題
【問題】
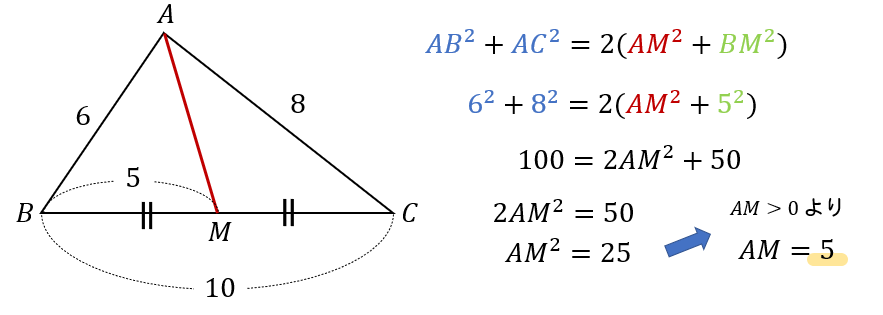
\(△ABC\) の辺\(BC\) の中点 \(M\) とする。
\(AB=6\), \(BC=10\), \(CA=8\) のとき,\(AM\) の長さを求めよ。
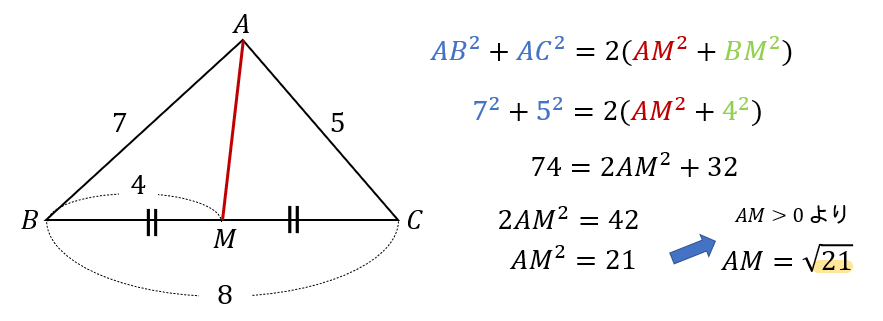
【問題】
\(△ABC\) の辺\(BC\) の中点 \(M\) ,辺 \(BM\) の中点 \(D\) とする。
\(a=8\), \(b=5\), \(c=7\) のとき,\(AM\), \(AD\) の長さを求めよ。
まとめ!
以上!
中線定理の使い方は理解してもらえましたか??
上で解いてもらった問題は、中線定理を使わずに余弦定理などを駆使して解を求めることができます。
しかし、中線定理を覚えておけば、かなり時短で解を求めることができます。
覚えるのが大変な定理でもないので、しっかりと覚えて使いこなせるようにしておきましょうね(/・ω・)/



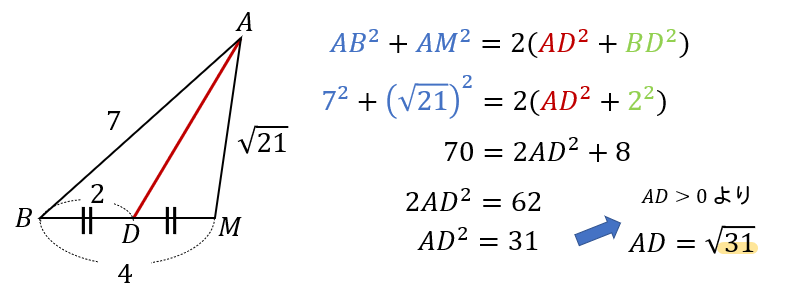














コメントを残す