こんにちは!数スタの小田です。
今回は高校数学Ⅱで学習する式と証明の単元から「不等式の証明、基礎パターン」についてイチから解説していきます。
等式の証明についてはこちらの記事で解説している通り、わりとシンプルな感じでしたね!
ですが、不等式の証明はちょっとクセがあるんですよね(^^;)
等式のときとは違ったやり方になっていくので、まずはその手順を確認していきましょう。
今回取り上げる問題はこちら!
【問題①】\(x>y\) のとき、次の不等式を証明しなさい。
$$3x-4y>x-2y$$
【問題②】次の不等式を証明しなさい。また、等号が成り立つときを調べなさい。
(1)\(x^2+9y^2≧6xy\)
(2)\(x^2-2x+y^2+4y+5≧0\)
(3)\(x^2+y^2≧xy\)
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
不等式の証明手順
不等式は次の手順で証明を進めていきます。
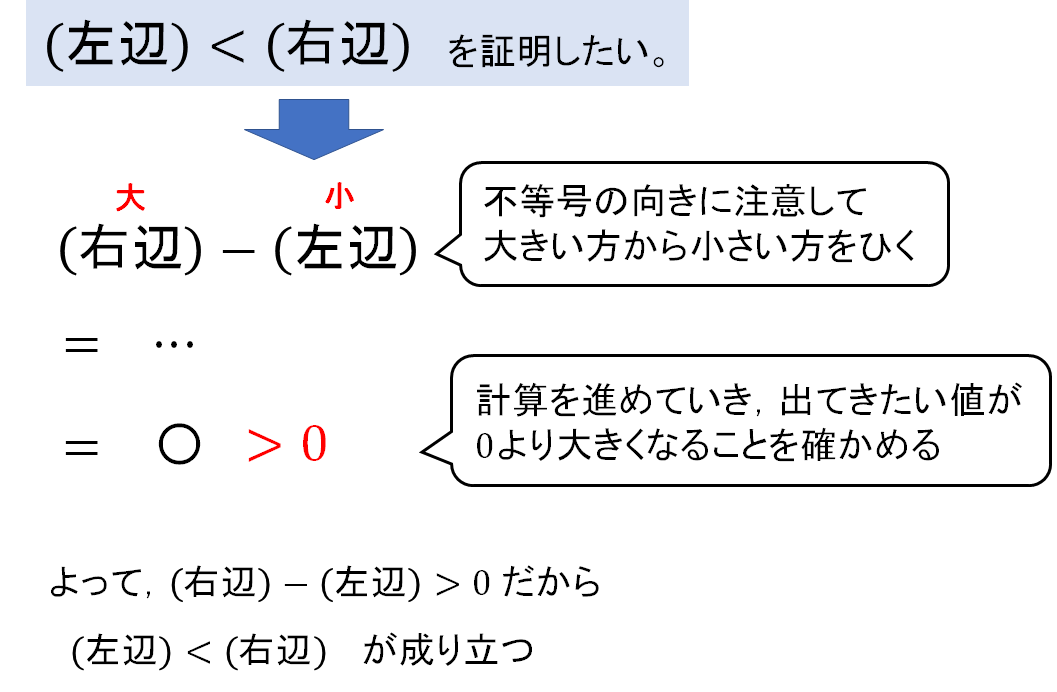
たいていの不等式は「大-小」のひき算からスタートしていくので、まずは差の式をつくること!
0より大きくなることを確かめるステップにおいては、いろんなパターンが存在するので、例題を通してやり方を確認していきましょう。
基礎パターン①(条件から)
【問題①】\(x>y\) のとき、次の不等式を証明しなさい。
$$3x-4y>x-2y$$
まずは (大)-(小) の式をつくってスタートです!

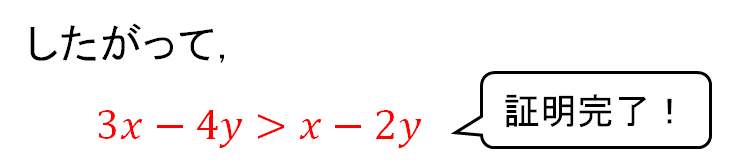
「~のとき」というように条件が与えられているときには、それらを使って「>0」となることを確かめていきましょう!
基礎パターン②(平方の性質から)
次の問題もパターン①と流れは同じ。
まずは(大)-(小)の計算からスタートしていきます。
ただ、「≧0」となるのを確かめる方法、等号が成り立つ条件を考えるという点について、新しい知識が必要となるので確認していきましょう!
(1)の解説
【問題②】次の不等式を証明しなさい。また、等号が成り立つときを調べなさい。
(1)\(x^2+9y^2≧6xy\)

条件式を利用したパターン①とは異なり、この問題では因数分解で2乗の形をつくることで0以上になることを確認しています。
証明が完了したら、次は等号が成り立つ条件を調べていきましょう。
ですが…

って感じている人もいるかもしれませんね(^^;)
等号が成り立つというのは、左辺と右辺が等しくなるときという意味です。

では、どこに注目すれば等号が成り立つ条件を見つけることができるかというと…
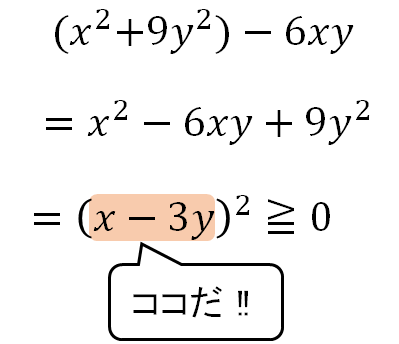
左辺、右辺の差を計算したときに「=0」となっていれば、左辺=右辺となります。
つまり、計算ででてきた2乗の中身に注目して、その部分が0になっていれば等号が成り立つことになります。
というわけで、

(2)の解説
【問題②】次の不等式を証明しなさい。また、等号が成り立つときを調べなさい。
(2)\(x^2-2x+y^2+4y+5≧0\)
右辺が0なので、そのまま左辺を変形して0以上になることを確かめていきます。
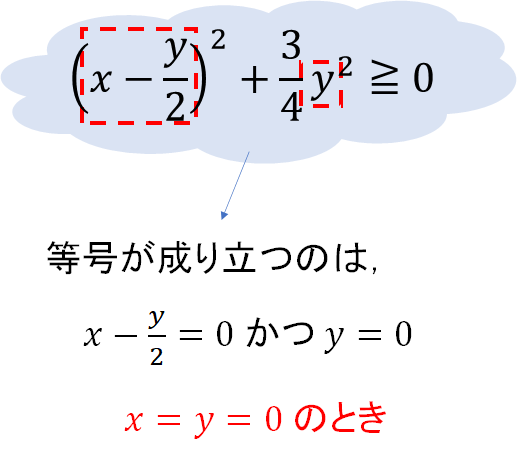
今回は因数分解ができないので、平方完成を利用して2乗の形をつくります。

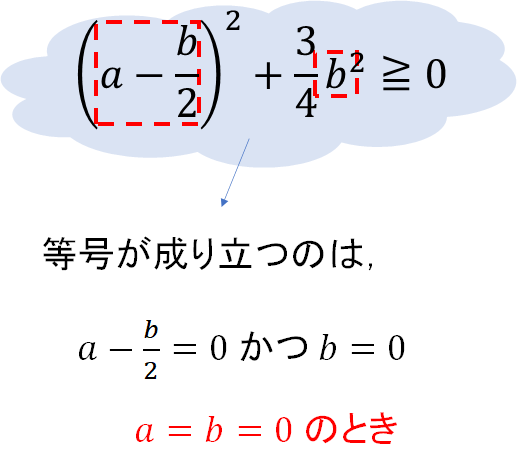
それぞれの2乗の中身が0になるときに等号が成り立つので

(3)の解説
【問題②】次の不等式を証明しなさい。また、等号が成り立つときを調べなさい。
(3)\(x^2+y^2≧xy\)
(大)-(小)の計算からスタートです!

それでは基礎パターンの手順について確認したところで、練習問題にチャレンジして理解を深めていきましょう!
練習問題にチャレンジ!
【問題①】\(a<1, b<1\) のとき、次の不等式を証明しなさい。
$$ab+1>a+b$$
【問題②】次の不等式を証明しなさい。
$$(a+3)^2>2(a+1)$$
【問題③】次の不等式を証明しなさい。また、等号が成り立つのはどんなときか求めなさい。
$$a(a+b)≦2a^2+b^2$$
メルマガ受講者さん向けに追加特訓課題を用意しました!
ここまでのところで不等式の証明(基本パターン)はバッチリになりましたか?
他にもルート、絶対値を含むパターン、相加相乗平均などのパターンもありますので、引き続き不等式の証明を特訓していきましょう!
しかし、不等式の証明にはいろんなパターンの解き方があるのでちょっとややこしいですよね(^^;
テストになると「どの解き方を使えばいいんだっけ?」と困ってしまうこともあるでしょう。
そこで、今回は不等式の証明のテスト対策課題として頻出パターンのランダム演習課題を用意しました。いろんなパターンをランダム形式で解いていくことで、知識の引き出し方を鍛えていこうというものです。

一通りの基礎を学んだあとに、こちらの課題に取り組めば知識をガチッと固めて、テストでも完答できるようになりますよ^^
こちらの課題はメルマガ講座の受講者さんに配布している限定サイトの中で公開しています。
メルマガ講座は無料で受講できますから、気軽にこちらから課題を受け取ってくださいね!
【追加演習】不等式の証明
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用ください^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
まとめ
お疲れ様でした!
練習問題はバッチリでしたか?これらができていれば不等式の証明基礎は大丈夫でしょう^^
次はちょっと発展的なルート、絶対値を含むパターンにチャレンジしていきましょう(‘ω’)ノ



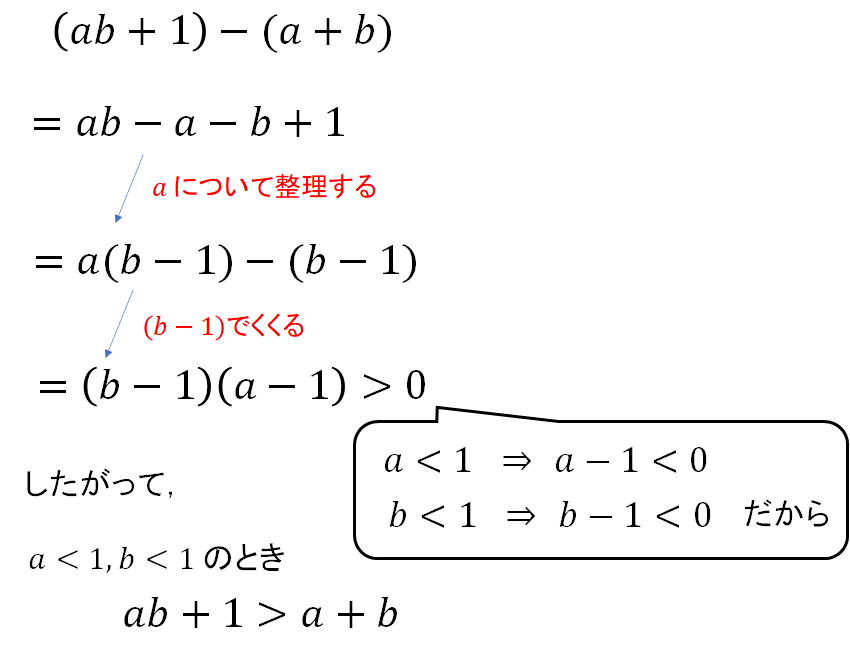














コメントを残す