こんにちは!数スタの小田です。
今回は高校数学Ⅱで学習する式と証明の単元から「ルートを含む不等式の証明」についてイチから解説していきます。
ちょっとしたコツが必要になるので、どのような発想で解いていくのかチェックしていきましょう!
取り上げる問題はこちらです。
【問題】\(x>0\) のとき、次の不等式を証明しなさい。
$$1+x>\sqrt{1+2x}$$
練習のところでいろんなパターンの証明を取り上げているので、そちらもチャレンジしてみてください!
今回の内容をサクッと理解したい方はこちらの動画がおススメです(‘ω’)ノ
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
ルートを含む不等式の証明手順
【問題】\(x>0\) のとき、次の不等式を証明しなさい。
$$1+x>\sqrt{1+2x}$$
ルートを含む不等式では、そのまま差を計算してしまうと途中で詰んでしまいます。

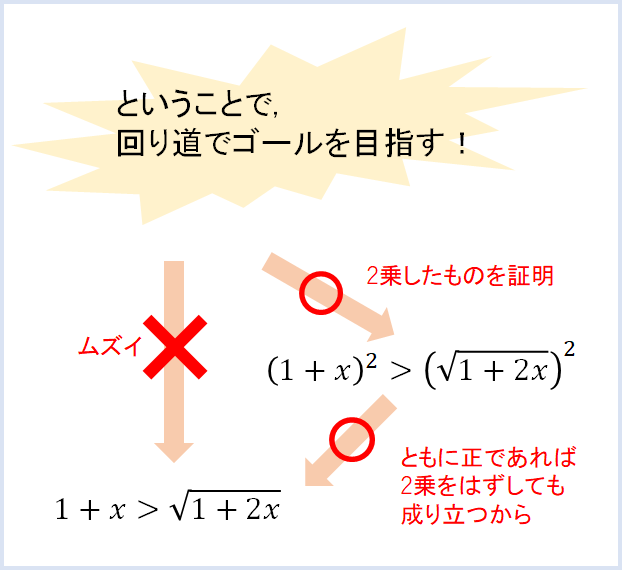
というわけで!
まずは\((1+x)^2>\sqrt{1+2x}^2\) が成り立つことを証明していきましょう。

これで2乗の形が証明できました。
次に2乗の中身がともに0以上になることを確認して、もとの不等式が成り立つことを証明しましょう!
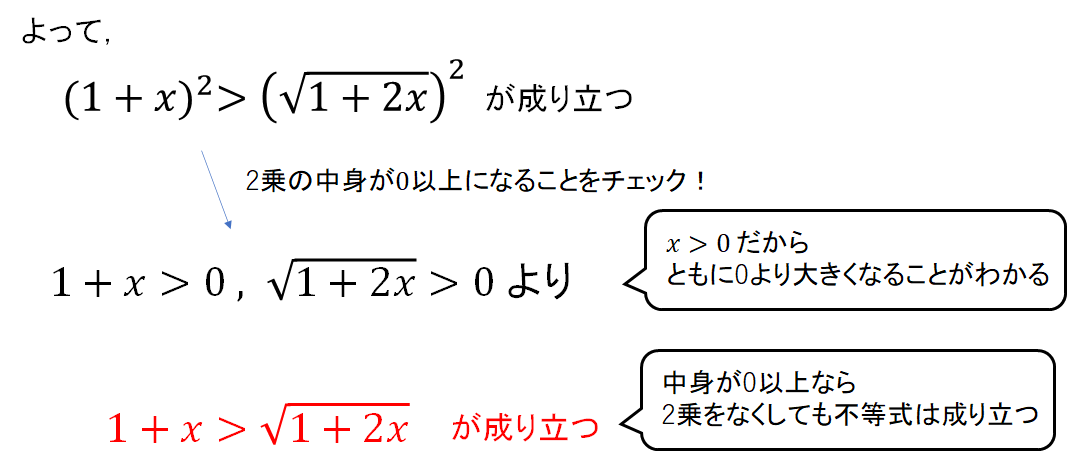
これで証明完成です!
流れは理解してもらえましたか?
- まずは2乗の形を証明
- 2乗の中身が0以上になることをチェックして2乗をとる
- もとの不等式の証明完成!
では、この証明手順に慣れるために次の練習問題にチャレンジしてみましょう。
練習問題にチャレンジ!
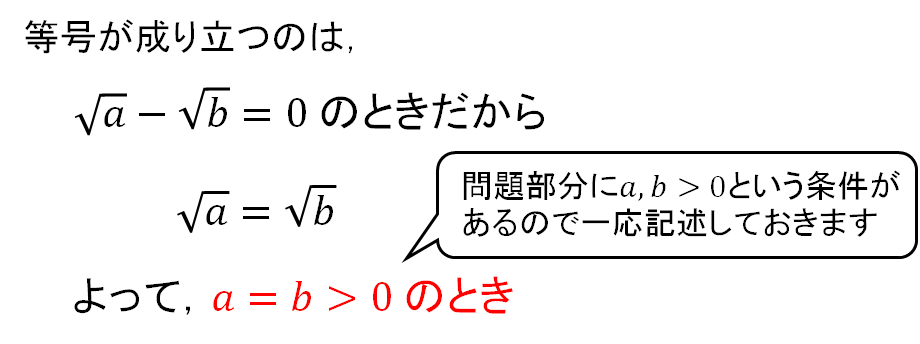
【練習①】\(a>0, b>0\) のとき、次の不等式を証明しなさい。また等号が成り立つのはどのようなときか求めなさい。
$$\sqrt{2(a+b)}≧\sqrt{a}+\sqrt{b}$$
【練習②】\(a>0, b>0\) のとき、次の不等式を証明しなさい。
$$3\sqrt{a}+2\sqrt{b}>\sqrt{9a+4b}$$
メルマガ受講者さん向けに追加特訓課題を用意しました!
ここまでのところで不等式の証明(ルートを含むパターン)はバッチリになりましたか?
他にも絶対値を含むパターン、相加相乗平均などのパターンもありますので、引き続き不等式の証明を特訓していきましょう!
しかし、不等式の証明にはいろんなパターンの解き方があるのでちょっとややこしいですよね(^^;
テストになると「どの解き方を使えばいいんだっけ?」と困ってしまうこともあるでしょう。
そこで、今回は不等式の証明のテスト対策課題として頻出パターンのランダム演習課題を用意しました。いろんなパターンをランダム形式で解いていくことで、知識の引き出し方を鍛えていこうというものです。

一通りの基礎を学んだあとに、こちらの課題に取り組めば知識をガチッと固めて、テストでも完答できるようになりますよ^^
こちらの課題はメルマガ講座の受講者さんに配布している限定サイトの中で公開しています。
メルマガ講座は無料で受講できますから、気軽にこちらから課題を受け取ってくださいね!
【追加演習】不等式の証明
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用ください^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
まとめ
お疲れ様でした!
ルートを含む不等式の証明では難しい計算もほとんどないので、しっかりと手順を覚えておけば大丈夫ですね!
- まずは2乗の形を証明
- 2乗の中身が0以上になることをチェックして2乗をとる
- もとの不等式の証明完成!
ルートがクリア出来たら次は絶対値にもチャレンジしてみてください(‘ω’)ノ
では、今回は以上!




















コメントを残す