【二次方程式】因数分解を利用した解き方を例題解説！

今回は、中3で学習する二次方程式の単元から

因数分解を利用して計算する方法

について解説していくよ！

二次方程式の解き方は、大きく分けて4パターンあります。

この中から

因数分解を利用して計算する方法について

例題を使いながら解説していきます。

この計算方法をマスターできれば、以下のような問題が解けるようになります。

各問題の解説は、記事途中で(^^)/

今回の記事はこちらの動画でも解説しています(/・ω・)/

因数分解を使ったやり方・考え方とは

さて、突然ですが！

上の式のように、掛け算の答えが０になるような計算式って

どんなものがあるかな？？

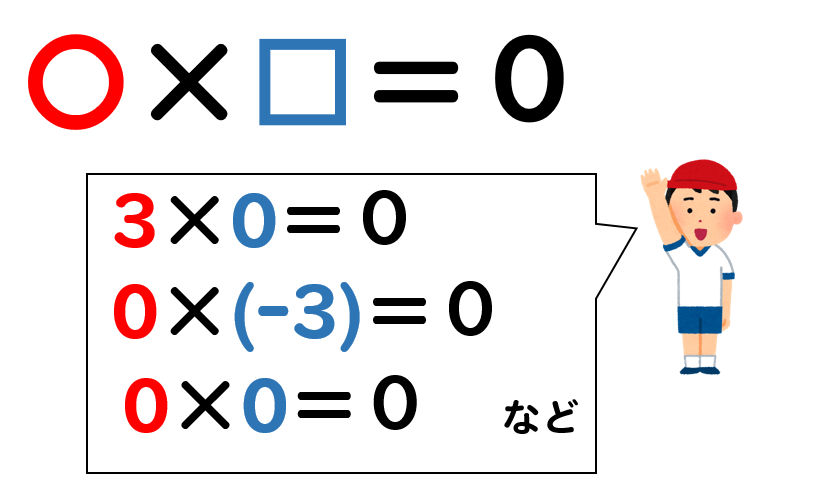
そうですね。

$$3\times 0=0$$

$$0\times (-3)=0$$

$$0 \times 0 =0$$

などなど、たくさんあるよね！

いくつか例を挙げてもらったけど

掛け算の答えが０になる計算式って

どんな共通点があるかわかるかな？

そうですね！！

掛け算の答えが0になるということは

必ず計算式の中に0が含まれているっていうことになるんですね。

二次方程式の因数分解を利用した解き方っていうのは

この性質を使って、解いていくことになるから

しっかりと理解しておきましょう。

掛け算の答えが0　⇒　式の中に0が含まれている

というのを教科書に載っているような表現で書き直すと

ということになります。

それでは、こちらの二次方程式を見てください。

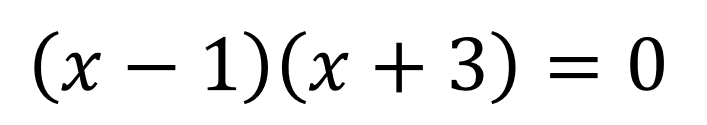
見た目こそちょっと複雑に見えますが

この式って、先ほど見てきた掛け算の式と同じなんですね。

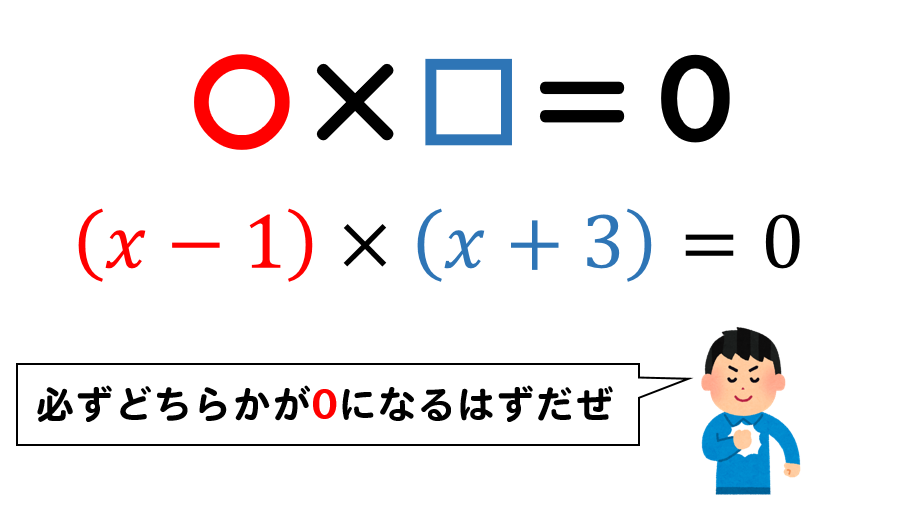
\((x-1)\)と\((x+3)\)を掛けたら0になるということなので

\((x-1)\)と\((x+3)\)のどちらかが0になるはずです。

ということから

$$x-1=0$$

$$x=1$$

$$x+3=0$$

$$x=-3$$

よって、この方程式の答えは\(x=1,-3\)

このように2つの答えを見つけることができました。

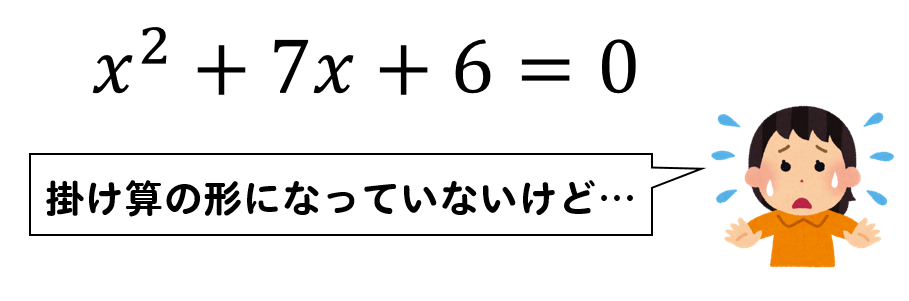
このように、掛け算の形になっていないような二次方程式でも

因数分解を利用することで

掛け算の形に変形することで、上の方程式と同様に解くことができます。

二次方程式で因数分解を利用して解くというのは

式を変形してA×B＝0の形を作り

そこからA=0、B=0という性質を利用して解いていく方法のことです。

それでは、この性質を利用して

上で紹介した例題の解き方を解説していきます。

因数分解を利用した二次方程式の例題解説！

（1）解説＆解答

この方程式は初めからAB=０の形が完成しているので楽勝です！

\((x-2)\)と\((x+3)\)を掛けると0になるということから

\((x-2)\)と\((x+3)\)のどちらかが0になるはずです。

よって

$$x-2=0$$

$$x=2$$

$$x+3=0$$

$$x=-3$$

（2）解説＆解答

こちらもAB=0の形が出来上がっているので

それぞれの掛けられている式を見ていくと

$$3x-2=0$$

$$3x=2$$

$$x=\frac{2}{3}$$

$$x+5=0$$

$$x=-5$$

（3）解説＆解答

この方程式はAB=0の形ができあがっていないので式変形が必要になります。

まずは＝０の部分を作るために

\(-4x\)を左辺に移項します。

$$x^2+4x=0$$

ここから左辺を因数分解します。

$$x(x+4)=0$$

AB=0の形ができあがったので

$$x=0$$

$$x+4=0$$

$$x=-4$$

（4）解説＆解答

AB＝0の形になるよう、左辺を因数分解しましょう。

$$(x-3)(x+2)=0$$

するとAB=0の形ができあがったので

$$x-3=0$$

$$x=3$$

$$x+2=0$$

$$x=-2$$

（5）解説＆解答

左辺を因数分解してAB=0の形を作りましょう。

$$(x+6)^2=0$$

あれ…ちょっと見た目が違うぞ…

ってなっちゃいますが、コレも考え方は一緒だからね。

$$(x+6)^2=0$$

\((x+6)(x+6)=0\)ってことだから

$$x+6=0$$

$$x=-6$$

となります。

この場合、他の二次方程式と違って

答えが1つしか出てこないのが特徴です。

因数分解をして\((   )^2=0\)の形になれば、答えは1つだけ！

というのも覚えておきましょう。

（6）解説＆解答

左辺を因数分解するのに邪魔な-3を消しましょう。

両辺を-3で割ってやると

$$x^2+2x-15=0$$

になって、わかりやすい式になりますね。

ここから因数分解をしてやると

$$(x+5)(x-3)=0$$

$$x+5=0$$

$$x=-5$$

$$x-3=0$$

$$x=3$$

（7）解説＆解答

パッと見た感じでは

AB=0の形になっているように見えますが

右辺が0ではないのでダメ！

式を展開してAB=0の形になるように式変形していきましょう。

$$x^2-6x+8=3x$$

$$x^2-9x+8=0$$

$$(x-8)(x-1)=0$$

$$x-8=0$$

$$x=8$$

$$x-1=0$$

$$x=1$$

注意！二次方程式と因数分解の違いをハッキリさせろ！

この記事を通して、二次方程式の因数分解を利用した解き方を学んでもらったと思います。

ここでちょっと注意しておきたいことがあります。

二次方程式の計算に慣れてくると、ちょっとした落とし穴があるんですね。

それは、次の問題で発生します。

答えは

$$x^2+x-56=(x+8)(x-7)$$

で終わりなのですが…

$$x^2+x-56=(x+8)(x-7)$$

$$x=-8,7$$

これは間違い！！

ここまでやっちゃう人が出てきちゃうんですね。

方程式とごちゃごちゃになってしまっているので

ちょっと整理しておきましょう。

しっかりと問題を読んで

因数分解をする問題なのか

方程式を解く問題なのか

ちゃんと見極めてくださいね。

数学がちょっと得意な人ほど陥りやすいミスなので

ほんっとに気を付けてください。

【追加演習プリント】自宅学習で伸ばしたい方へ！

この記事を読んでくださっている保護者さんの方へ！

ここで紹介してる例題を一通り理解してもらえれば、因数分解を利用した解き方はバッチリです＾＾

あとは実戦演習を通して、手本がなくてもスラスラと解けるようにしておいてもらいたいです！

というわけで、自宅学習で活用してもらいたい演習プリントを用意しました。

ここで取り上げている問題はこちら！

問題＆解説をプリント形式で用意しているので、こちらを印刷してお子さんに渡してあげてください＾＾

10分ほどで取り組める分量になっているので、スキマ時間を活用して二次方程式の理解度を高めておきましょう！

勉強のスタート時に小テストとして取り組んでみると、イイ感じに集中力が高まって、その日の学習がスムーズになってくるかもしれませんね(‘ω’)ノ

追加演習をやってテストの点数をUPさせたい方には、課題プリントをメールで送らせてもらっています。

「名前（ニックネームでOK）」「メールアドレス」を入力すれば無料で受け取れますので気軽にご活用くださいね＾＾

（ご登録いただいたメールアドレスに教材を送らせていただきます）

ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定！

このメルマガは簡単に配信解除できますので、気軽にご活用ください＾＾

まとめ

お疲れ様でした！

今回は二次方程式の因数分解を利用した解き方について解説しましたが理解が深まりましたでしょうか。

AB=0の形を作るというのが

因数分解を利用した解き方では大切なポイントでした。

式変形や因数分解は慣れが必要になってくるので

とにかく練習問題を繰り返して

解き方を身につけていきましょう！

ファイトだー(/・ω・)/

二次方程式の解き方4パターンについてはこちらをどうぞ！

• 平方根の考えを利用して解く
• 因数分解を利用して解く　⇐ 今回の記事
• 解の公式を利用して解く
• 平方完成を利用して解く