こんにちは!数スタの小田です。
今回は中3で学習する『因数分解』の単元から
共通因数でくくる
というやり方について解説していきます。
共通因数でくくるというのは、因数分解の入門編みたいな感じですのでサクッと理解しちゃいましょう!
また、共通因数のくくり方については理解しているけど、マイナスの場合にはどうするの?という方に向けての解説もおこなっていきます。

【因数分解】共通因数ってなに?
そもそも共通因数ってなに?っていうことについて考えてみましょう。
その名のとおりですが
共通な因数
のことを共通因数といいます。
そのまんまじゃん!って感じですが、ちょっと説明を入れていきますね。
まず、因数とは

このように、数や式を積の形で表したときのパーツ部分のことを因数といいます。
\(10=2\times 5\) と表したとき、2と5は10の因数
\(x^2+5x+4=(x+4)(x+1)\) と表したとき、\((x+4)\) と \((x+1)\) は\(x^2+5x+4\) の因数
ってことですね。
では、共通因数とは

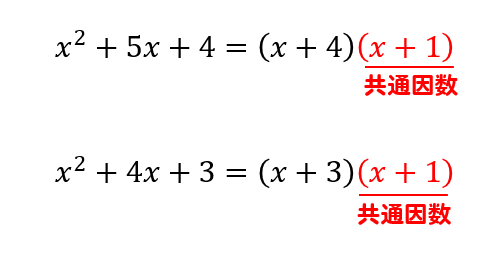
このようにそれぞれの因数を見比べたとき、共通しているもののことを共通因数といいます。
ちょっと具体例を見てみましょう。
\(12a^2b\) と \(18ab^2\) の共通因数は?

このように共通因数を見つけることができます。
慣れてくれば、簡単に見つけれるようになりますが、初めのうちは数を素因数分解して見比べてみるといいですね(^^)
【因数分解】共通因数のくくり方
式の中に共通因数がある場合、次のようにくくりだすことができます。

共通因数をかっこの外につけて、残りモノをかっこの中にいれる。
これを共通因数でくくりだす因数分解といいます。
それでは、ここから共通因数でくくる因数分解についていろいろな例題を通して確認していきましょう。
【因数分解】共通因数をくくる例題
例題①
次の式を因数分解しなさい。
$$2xy+4x$$

共通因数を見つけるのに慣れるまでは、このようにそれぞれを分解してやると見つけやすいですね。
同じパーツはかっこの外に出して、残りモノはかっこの中に入れる。
たったこれだけです(^^)
例題②
次の式を因数分解しなさい。
$$4x^2y-6xy^2+2xy$$
項が増えても考え方は同じです。
3つの項に共通している因数を見つけます。
すると、\(2xy\) という共通因数が見つかるので
$$4x^2y-6xy^2+2xy$$
$$=2xy\times 2x-2xy\times 3y+2xy\times 1$$
$$=2xy(2x-3y+1)$$
例題③ マイナスがある場合
次の式を因数分解しなさい。
$$-2x^2+4xy$$
今回の式のように先頭にマイナスがついている場合
$$-2x^2+4xy=-2x(x-2y)$$
このようにマイナスも一緒に共通因数としてくくりだすのが一般的です。
$$-2x^2+4xy=2x(-x+2y)$$
これでも間違いではないんだけど、かっこの先頭にある数にマイナスがついていると…
なんか違和感!
と感じる人も多いので、数学の美しさ的には共通因数としてマイナスも一緒にくくりだし、マイナスはかっこの外につけるのが一般的ではあります。
それと!
マイナスでくくりだす場合には、かっこ内の符号に注意が必要です。
$$-2x^2+4xy=-2x(x-2y)$$
$$-3x^2-9xy=-3x(x+3y)$$
マイナスでくくると、このようにかっこ内の符号は逆転してしまいますね。
そこをミスしないように気をつけてくださいね。
例題④ 応用編
次の式を因数分解しなさい。
$$xy+2x+y+2$$
この問題は応用になりますので、共通因数のくくりだしに慣れてきた方は挑戦してみましょう。
まずは、式のこの部分を見て共通因数をくくりだします。
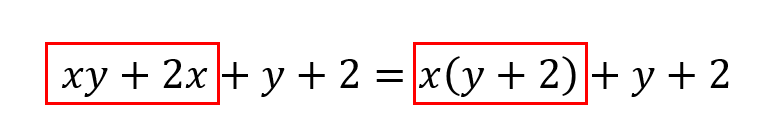
すると、次のようにして
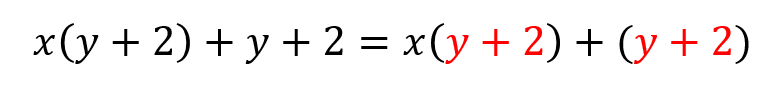
\((y+2)\) が共通因数だ!ってことに気が付けます。
共通因数を見つけることができれば、くくりだせばOK!ということで
$$xy+2x+y+2=x(y+2)+(y+2)$$
$$=(y+2)(x+1)$$
このように因数分解をすることができます。
このような応用問題については、こちらの記事で詳しく解説しているので興味がある方は見ていってください(^^)

練習問題で理解をチェック!
それではここまでの内容がちゃんと理解できているか練習問題にチャレンジしてみましょう。
では、全部で5題!
それぞれの式を因数分解してみましょう。
【問題①】

【問題②】
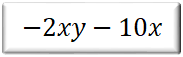
【問題③】
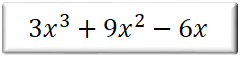
【問題④】
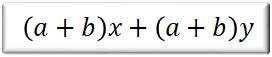
【問題⑤】
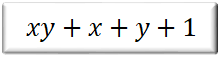
【特典】これやっといてください!
ここまでのところで共通因数のくくり出しについては理解してもらえたと思うんですが…
もうちょっとだけ頑張ってください!!
最後にやった「置き換えを利用する」やつ、これはテストになるとできなくなっちゃう人が続出しちゃうんですね…汗(ちょっと難しめだからやり方を忘れちゃうのかな><)
ってことで、僕が教えている学生さんにはテスト前にサクッと見直しができるポイントまとめ&演習プリントを渡しています。
これをテスト前にパッと見ることで、やり方を一気に思い出せるので、もったいないミスを防いで確実に点が取れるようになるんです^^
今回はこの記事を最後まで取り組んでくれたお礼として、このプリントを配布するのでテスト前の見直しに活用してください(‘ω’)ノ
「名前(ニックネームでOK)」「メールアドレス」を入力すれば無料で受け取れます^^
(ご登録いただいたメールアドレスに教材を送らせていただきます)
ご登録いただいたメールアドレス宛に随時、基礎力をアップさせる演習課題をお届けしていく予定!
このメルマガは簡単に配信解除できますので、気軽にご活用ください^^
【因数分解】共通因数でくくるやり方まとめ!
お疲れ様でした!
以上、共通因数でくくり因数分解のやり方でした。
共通因数でくくるというのは、ちょっと慣れが必要かもしれませんが何度も練習していれば苦労なく解くことができるようになります。
やり方が分かれば、あとは練習あるのみだ!
因数分解の超難問についても、こちらでまとめているので
>【高校入試】因数分解の難問を解説!難関高校の入試問題に挑戦しよう!
ぜひとも、このレベルが解けるようになるまで練習を重ねていってください!
ファイトだ(/・ω・)/



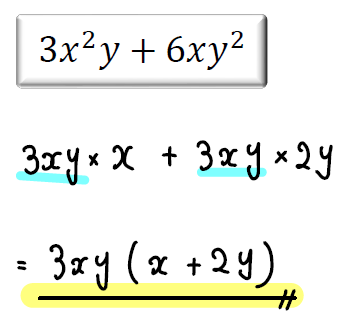
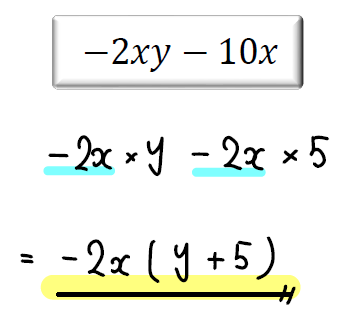
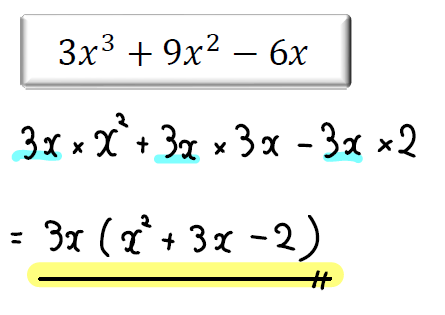
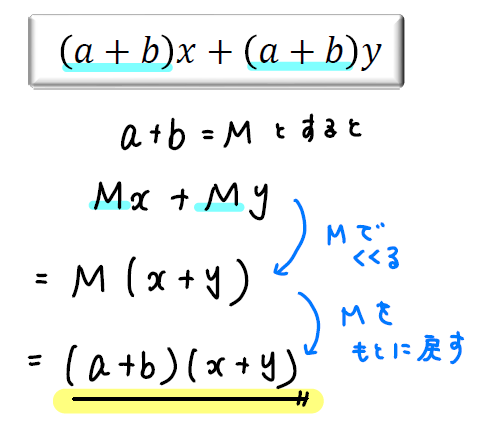















コメントを残す