今回は中2数学で学習する一次関数の単元から「水そうの利用問題」について取り上げます。
ちょっと発展的な問題ですが、これをクリアするとかなり力をつけることができます！
以下の3パターンについて解法をチェックしていくので、それぞれのポイントをおさえていきましょう(‘ω’)ノ
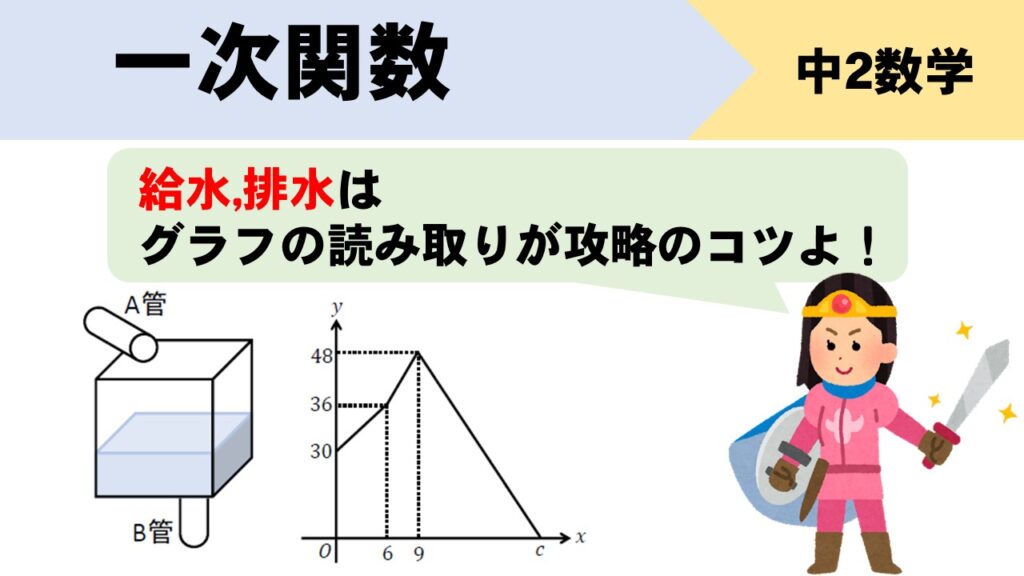
【給水、排水パターン】
30L入っている水そうに、毎分\(a\)Lの割合で水を給水するA管と、毎分\(b\)Lの割合で水を排水するB管がついている。A管とB管を同時に開いて給水を始め、6分経過してからB管を閉じた。その3分後にA管を閉じ、B管だけを開いて、水そうの水がなくなるまで排水した。下のグラフは給水を始めてから\(x\)分後の水そう内の水の量を\(y\)Lとして、\(x\)と\(y\)の関係を表したものである。
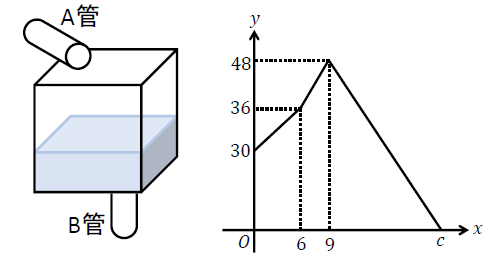
（1）\(a,b\)の値を求めなさい。
（2）グラフの\(c\)にあてはまる数を求めなさい。
（3）0分から6分、6分から9分、9分から\(c\)分のときの直線の式をそれぞれ求めなさい。
【おもりが入っているパターン】
縦40㎝、横50㎝、高さ30㎝の直方体の形をした水そうの中に、1辺が20㎝の立方体のおもりが入っています。この水そうに毎分2Lの割合で満水になるまで水を入れるとき、入れはじめてから\(x\)分後の水そうの底から水面までの高さを\(y\)cmとします。
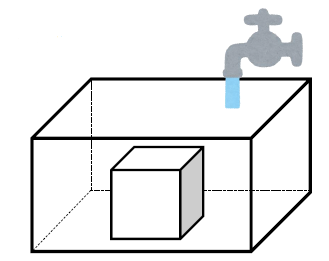
（1）\(y\)の変域が\(0≦y≦20\)のときの、\(x\)の変域を求めなさい。また、\(x,y\)の関係を式に表しなさい。
（2）\(y\)の変域が\(20≦y≦30\)のときの、\(x,y\)の関係を式に表しなさい。
【仕切りがあるパターン】
図のような直方体の形をした容器がある。2枚の仕切りを使って容器を区切るとき、底面のうち、2枚の仕切りにはさまれた部分を底面Aとする。この容器の左のスペースに毎分3Lの割合で水を入れるとき、水を入れ始めてから\(x\)分後の底面A上での水面までの高さを\(y\)cmとするとき、水を入れ始めてから満水になるまでのグラフを完成させなさい。
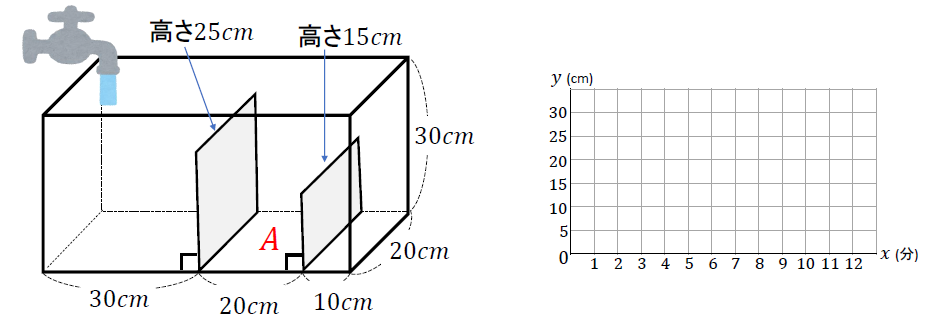
それぞれの問題には解説動画もつけているので、あわせてご活用ください！
給水、排水のグラフ読み取り
30L入っている水そうに、毎分\(a\)Lの割合で水を給水するA管と、毎分\(b\)Lの割合で水を排水するB管がついている。A管とB管を同時に開いて給水を始め、6分経過してからB管を閉じた。その3分後にA管を閉じ、B管だけを開いて、水そうの水がなくなるまで排水した。下のグラフは給水を始めてから\(x\)分後の水そう内の水の量を\(y\)Lとして、\(x\)と\(y\)の関係を表したものである。
（1）の解説
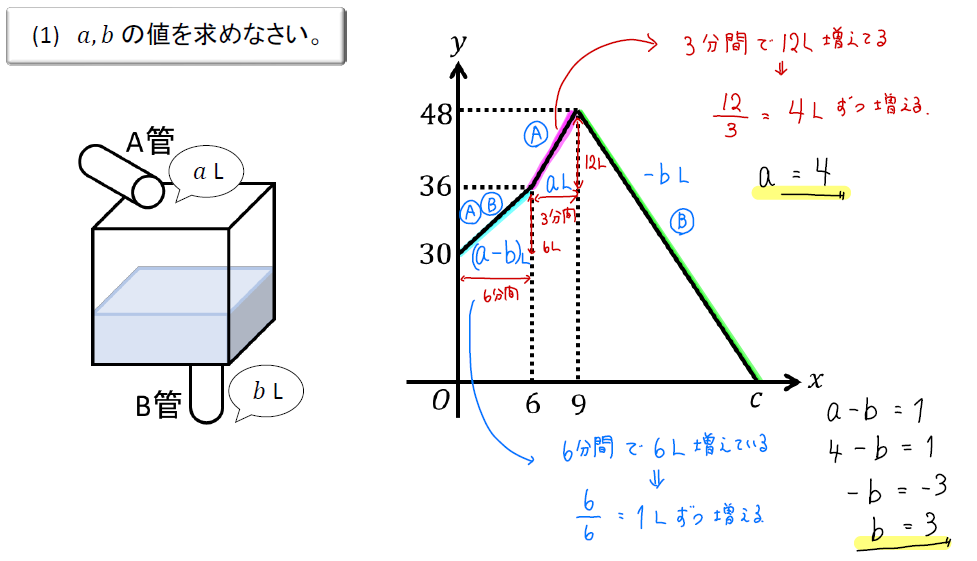
それぞれの区間において、毎分どれくらいの量の水が変化しているのか読み取りましょう。
0分～6分の間は給水、排水を同時におこなっているので毎分\((a-b)\)Lずつ水が増える。
6分～9分の間は給水だけだから毎分\(a\)Lずつ水が増える。
9分～\(c\)分の間は排水だけだから毎分\(b\)Lずつ水が減る。減っていくので\(-b\)Lと表しておきますね。
次に6分～9分の区間に注目すると、3分間に12Lの水が増えているので、\(12\div 3=毎分4L\)だけ水が増えていることがわかります。
このことから、\(a=4\)になることが求まりますね！
次に0分～6分の区間に注目します。
ここでは6分間で6L増えているので、\(6\div 6=毎分1L\)だけ水が増えていることがわかります。
このことから、\(a-b=1\) となり、\(a=4\) だから、\(b=3\)とわかります。
答え
$$a=4, b=3$$
（2）の解説
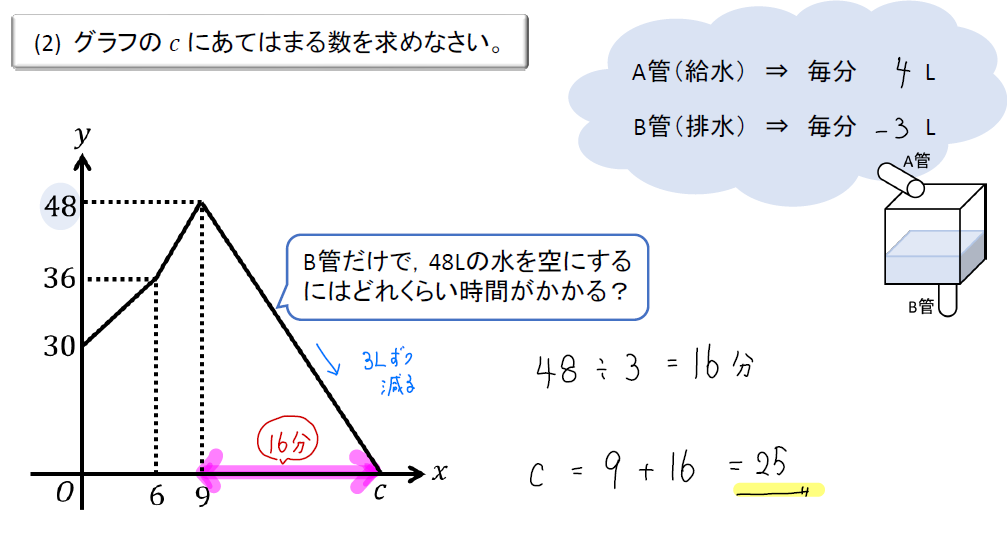
グラフ\(c\)のところは「水そうが空になる時間」を表しています。
では、排水が始まった9分の時点でとれくらいの水が入っていたかチェックすると、48Lだとわかります。
（1）より毎分3Lずつ排水していることがわかっているので、48Lの水を空にするためには、
$$48\div 3=16分$$
このように16分の時間がかかることがわかります。
よって、9分の時点から16分後に水そうが空になるので、\(c=9+16=25分\)となります。
答え
$$c=25$$
（3）の解説
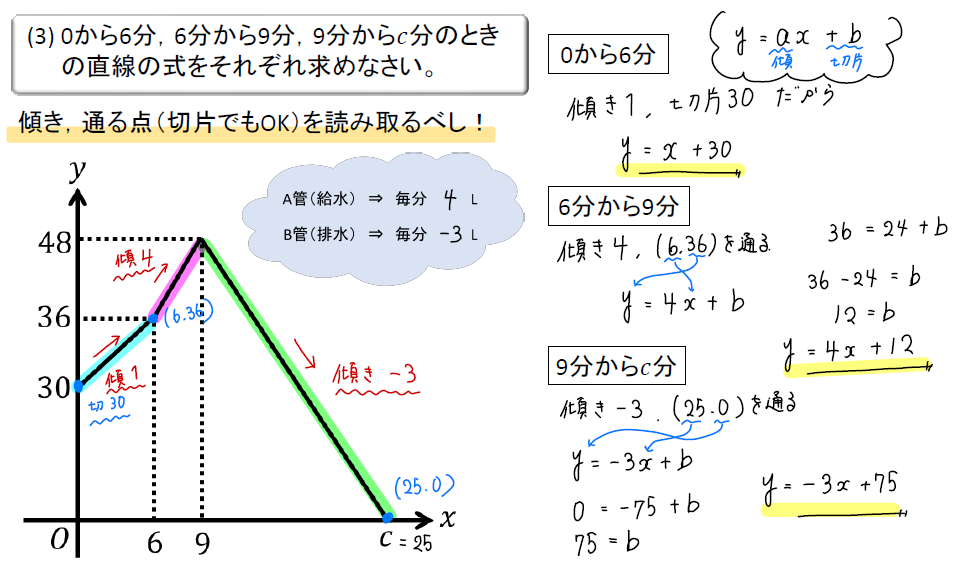
グラフから式を作るためには傾き、通る点（切片でもOK）を読み取ることが大事です！
0分～6分の区間においては、切片（\(y\)軸との交点）が30であると簡単に読み取れます。
さらに給水と排水が同時に行われており、毎分1Lずつ増えていく区間なので傾きは1と考えます。
よって、傾きが1で切片が30なので直線の式は\(y=x+30\)となります。
6分～9分の区間では、傾きは4（毎分4Lずつ増えるから）とすぐに読み取れますが、切片はパッと見で判断できません。
そこで、切片の代わりにこの区間の座標をどこでもいいので1つ読み取ります。
今回は区間の左端である\((6,36)\)を使います。
つまり、傾きが4で\((6,36)\)を通る直線の式ということだから
$$\begin{eqnarray}y&=&4x+b\\[5pt]x&=&6,y=36を代入\\[5pt]36&=&24+b\\[5pt]12&=&b \end{eqnarray}$$
よって、切片が12と分かったので直線の式は \(y=4x+12\) となります。
最後に9分～25分の区間について。
ここでは毎分3Lずつ減っていくので傾きは\(-3\)ですね。
（マイナスを忘れないように！）
切片の読み取りが難しいので、区間の右端である\((25,0)\)を使います。
つまり、傾きが\(-3\)で\((25,0)\)を通る直線の式ということだから
$$\begin{eqnarray}y&=&-3x+b\\[5pt]x&=&25,y=0を代入\\[5pt]0&=&-75+b\\[5pt]75&=&b \end{eqnarray}$$
よって、切片が75と分かったので直線の式は \(y=-3x+75\) となります。
答え
0分～6分 ⇒ \(y=x+30\)
6分～9分 ⇒ \(y=4x+12\)
9分～\(c\)分 ⇒ \(y=-3x+75\)
直方体の中におもりが入っている
縦40㎝、横50㎝、高さ30㎝の直方体の形をした水そうの中に、1辺が20㎝の立方体のおもりが入っています。この水そうに毎分2Lの割合で満水になるまで水を入れるとき、入れはじめてから\(x\)分後の水そうの底から水面までの高さを\(y\)cmとします。
（1）の解説
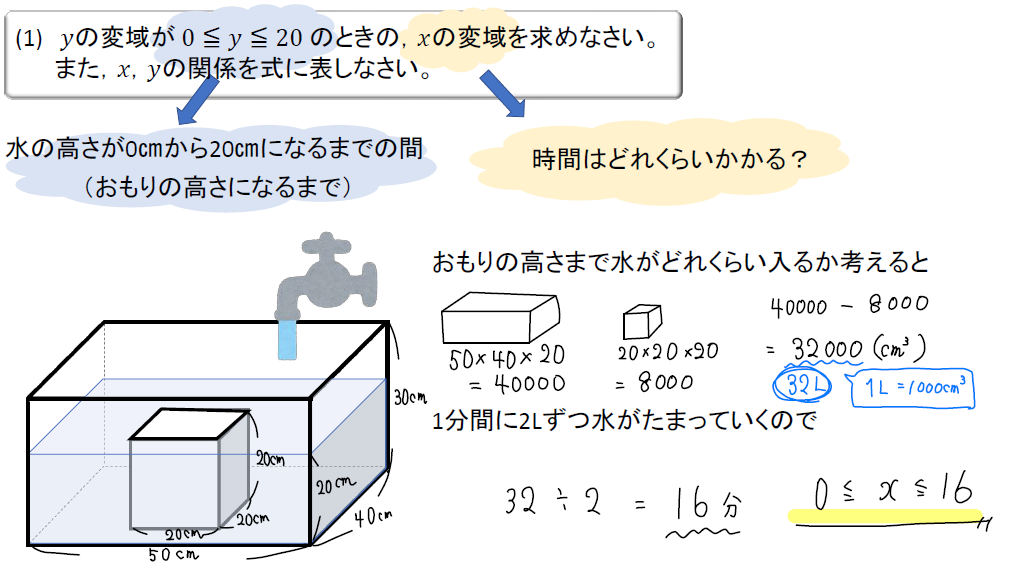
まずは問題で問われていることをかみ砕いて理解してみましょう。
今回問われているのは、
\(0≦y≦20\) ⇒ 水の高さが0㎝から20㎝になるまでの間（おもりの高さになるまで）
\(x\)の変域 ⇒ 時間はどれくらいかかる？
ということです。
ですので、おもりの高さまで水がどれくらい入るのかを考えてみましょう。
高さ20㎝の直方体の体積から、おもりの体積を除くと\(32000\)㎤と求まるので32Lの水が入ることがわかります。（1000㎤＝1L）
1分間に2Lずつの水がたまっていくので、おもりの高さまで水を入れるのに \(32\div 2=16分\)かかることになります。
よって、問われている\(x\)の変域（時間がどれくらいかかるか）というのは、\(0≦x≦16\)となるわけですね！
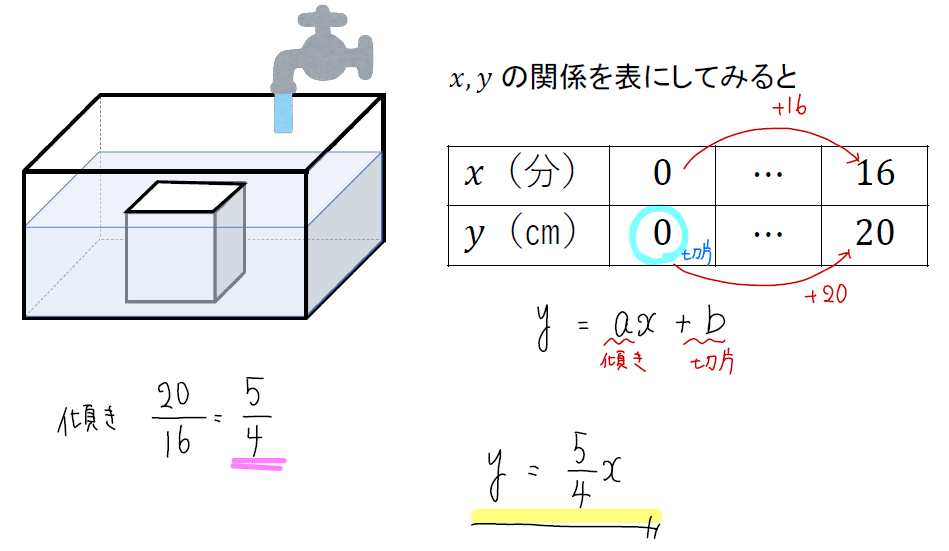
次に、このときの\(x,y\)の関係を式に表していきましょう。
図を見ているだけでは分かりにくいので、わかっていることを表にまとめてみるのがおススメです！
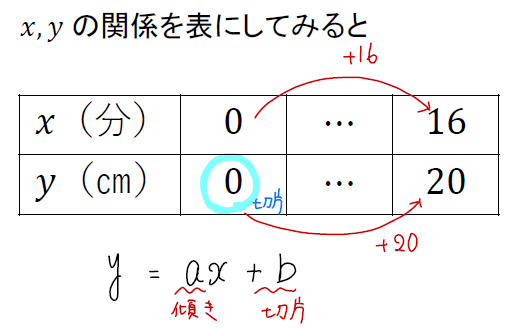
水の高さは一定の割合で変化していくと考えられるから「一次関数の式」を活用すればOKです。
そして、この表から切片と傾きを読み取りましょう！
切片は\(x=0\)のときの\(y\)座標のことだから0。
傾きは\(\frac{yの増加量}{xの増加量}\)だから\(\frac{20}{16}=\frac{5}{4}\)となります。
（これは1分間に\(\frac{5}{4}\)cmずつ水の高さが増えていくことを表しています）
よって、一次関数の式に当てはめていくと\(y=\frac{5}{4}x\)となります。
答え
$$0≦x≦16$$
$$y=\frac{5}{4}x$$
（2）の解説
\(20≦y≦30\) ⇒ 水の高さが20㎝から30㎝になるまでの間（おもりの高さをこえてから満水になるまで）
\(x,y\)の関係を式にする ⇒ \(y=\cdots \)の式を作る
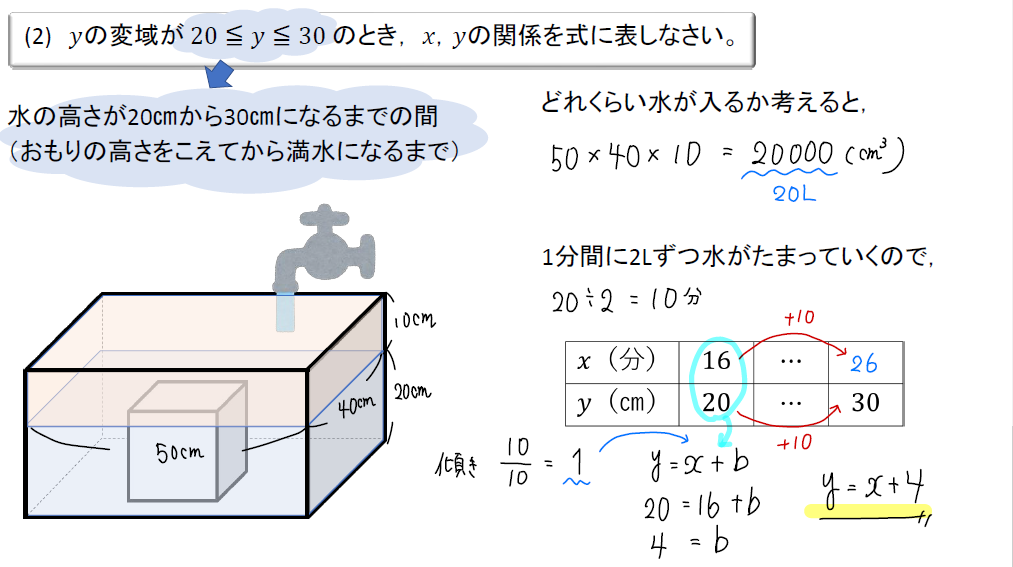
では、水の高さが20㎝から30㎝になるまでの間にどれくらいの水が入り、どれくらいの時間がかかるのかをチェックしましょう。
すると、水の量は体積は20000㎤なので20L。
1分間に2Lずつたまるので、\(20\div 2=10分\)の時間がかかることがわかります。
これらの関係を表にまとめるとこんな感じ！
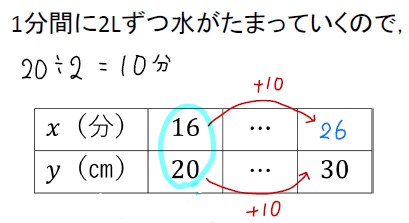
※水の高さが30㎝となるのは、16分の10分後なので26分。
まずは傾きを読み取ります。
すると、\(\frac{10}{10}=1\)とわかります。
そして、残念ながらこの表からは切片が読み取れないので…
代わりに座標を1つ読み取ります。今回は\(x=16, y=20\) を活用します。
つまり、傾き1で\(x=16, y=20\) となる直線の式を求めればいいということなので
$$\begin{eqnarray}y&=&x+b\\[5pt]x&=&16,y=20を代入\\[5pt]20&=&16+b\\[5pt]4&=&b \end{eqnarray}$$
よって、切片が4と分かったので直線の式は \(y=x+4\) となります。
答え
$$y=x+4$$
水そうの中に仕切りがある
まずはどのように水がたまっていくのかをイメージしておきましょう！
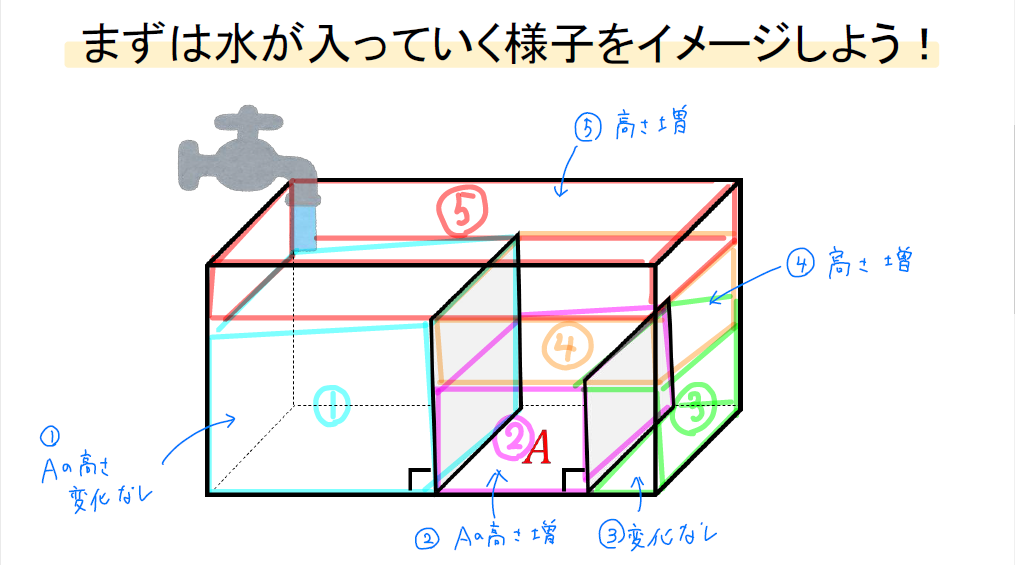
このように水のたまり方は、
① ⇒ ② ⇒ ③ ⇒ ④ ⇒ ⑤
5つのブロックに分けて考えられます。
さらに、赤字をつけた②④⑤のブロックに水が溜まっているときにAの高さが増えていくことも分かります。
そのことを踏まえて各ブロックごとに分割してグラフを考えていきましょう。
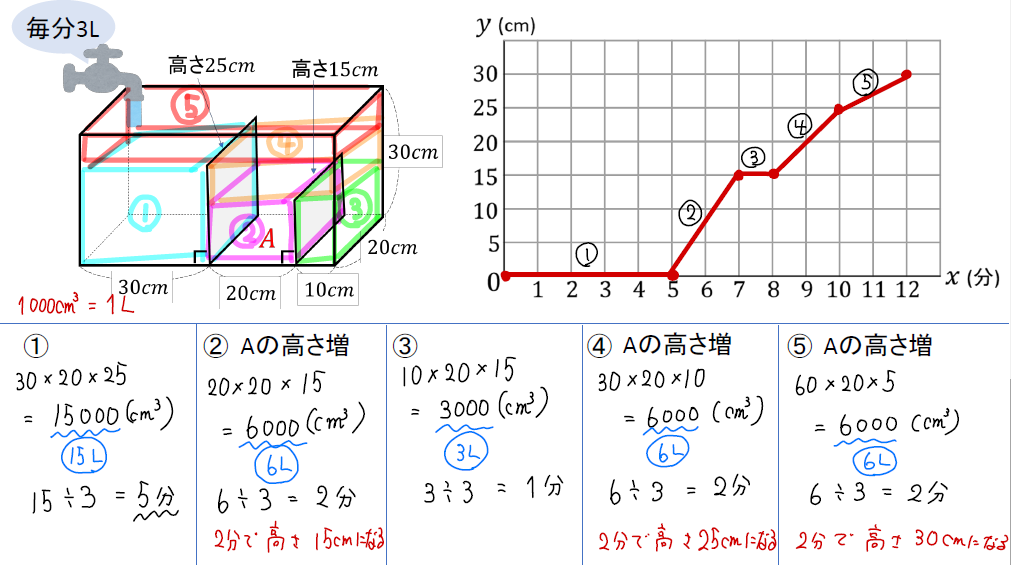
①のブロックをいっぱいにするには5分かかりますが、この間はAの高さは変化しません。
なので、0～5分の間はずっと高さ0㎝のまま真横の直線となります。
②のブロックは2分でいっぱいになります。つまり、2分で高さが15㎝まで上昇するということです。
よって、グラフでは2分で15㎝上昇するように右上がりの直線を書き込みます。
③のブロックは1分でいっぱいになりますが、Aの高さは変化しないので15㎝のまま真横に直線を書き入れます。
④のブロックでは2分でいっぱいになり、Aの高さは25㎝まで上昇します。
よって、2分後に25㎝となるように直線をつなげていきます。
⑤のブロックでは2分でいっぱいになり、Aの高さは30㎝（満水）となります。
よって、2分後に30㎝となるように直線をつなげればグラフの完成！
答え
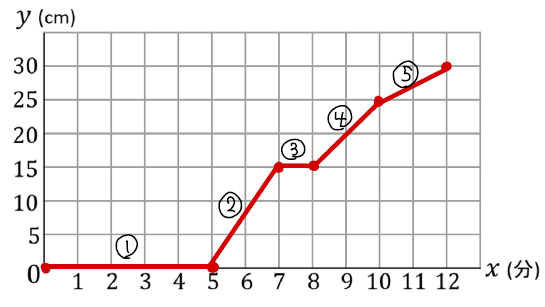
まとめ
お疲れ様でした！
今回はちょっと難しめな問題を取り上げてみましたが、いかがだったでしょうか。
どの問題においても特別な公式を覚えるってことはありません。
しっかりと問われていることを理解し、グラフや図から正確な情報を読み取れるかが大事なポイントです＾＾
そのためにはたくさんの問題をといて経験値をためていくことが大事ですので、今回の問題演習をキッカケにしてどんどんいろんな問題にチャレンジしてもらえると嬉しいです！
コメントを残す