【三角形の辺と角の大小関係】どの角、辺が大きくなる？基本問題の解き方をイチから！

こんにちは！数スタの小田です。

今回は高校数学Aで学習する図形の単元から「三角形の辺と角の大小関係」について取り上げます。

 

サクッと理解したい方は、こちらの動画も参考にしてください！

※動画内では（3）の答えがC＜B＜Aで終わっていますが、辺の大小関係を求めていませんでした…正しくはAB＜AC＜BCとなります。もしくは（3）は角の大小を考える問題だとしてください。

三角形の辺と角の大小関係のポイント

ここでおさえておきたいのは、辺と角の大小は対応しているということです。

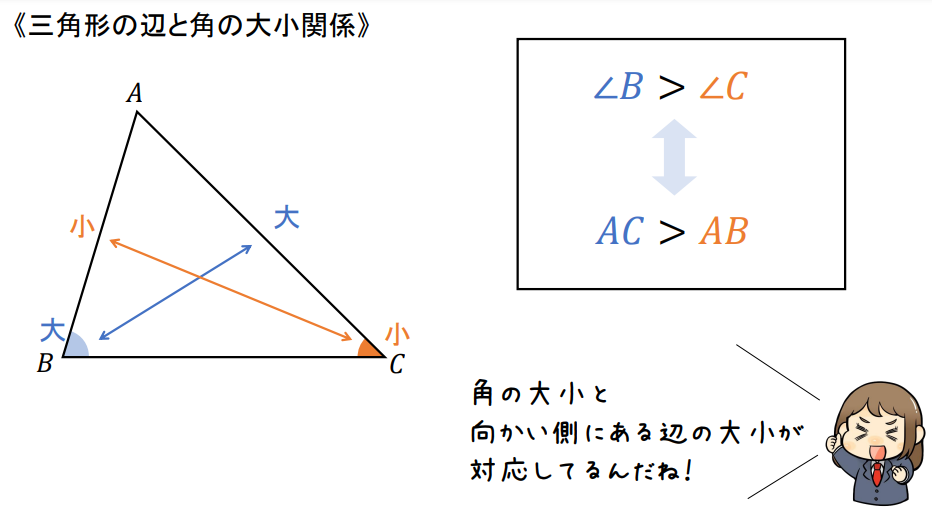
このように最大角の向かいにある辺は最大、最小角の向かいにある辺は最小になります。

このことを覚えておけば、今回の問題は楽勝ですよ(‘ω’)ノ

角、辺の大小関係を調べる！

（1）の解説　角の大小

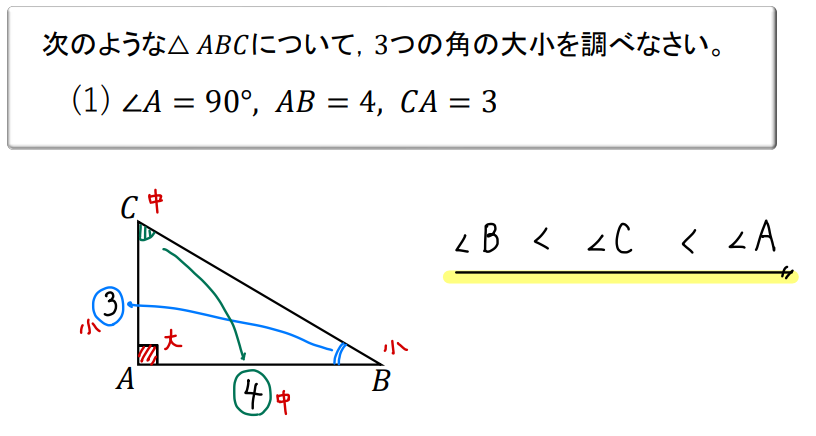
まず、\(∠A=90°\)に注目しましょう。

三角形の内角において、90°以上の角は確実に最大角となります。（内角の和は180°だもんね！）

なので、問題文を読んだ時点で

小：BまたはC　　中：BまたはC　　大：A

このような関係性が確定します。

 

というわけで、残りのB、Cの大小関係を調べるためにそれぞれの向かいにある辺の大きさを比較しましょう。

Bの向かいの辺　⇒　\(CA=3\)

Cの向かいの辺　⇒　\(AB=4\)

それぞれ比較してみると、（Bの向かいの辺）＜（Cの向かいの辺）となっているので、この辺の関係性がそのまま角の大小関係となり、\(B < C\) となります。

よって、\(∠B＜∠C＜∠A\) と判断することができますね！

（2）の解説　辺の大小

三角形の内角の和は180°なので、\(∠C=70°\) となりますね！

3つの角の大きさがわかったので、角の大小を比べてみると、\(∠A<∠B<∠C\) だとわかります。

よって、\((∠Aの向かいの辺)<(∠Bの向かいの辺)<(∠Cの向かいの辺)　⇒　CB<AC<AB\) と判断することができます。

かんたんですね＾＾

（3）の解説　辺の大小

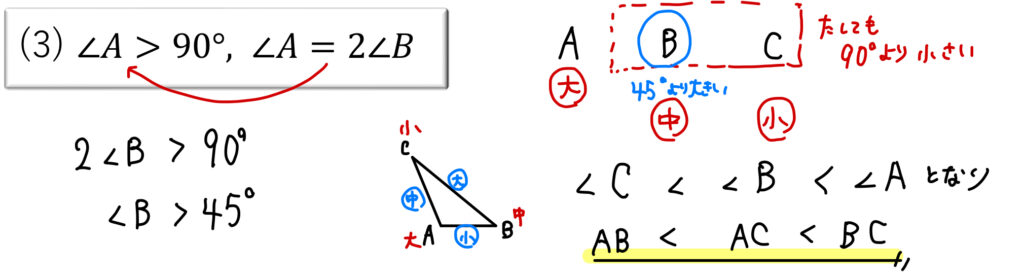
ここでつまづいた人が多かったかもしれませんね(^^;)

なんだか見た目が難しそうですが…落ち着いて考えれば楽勝です！

 

(1)の解説でお伝えしたように、三角形の内角において90°以上の角は最大が確定します。

よって、\(∠A>90°\) なので、Aが最大であることはすぐにわかります。

 

次に\(∠A=2∠B\)と\(∠A>90°\)より、\(∠B>45°\)となります。

\(∠A>90°\)ということは、内角の和が180°であることから \(B+C<90°\) です。

 

【BとCの和が90°より小さい】

【Bが45°よりも大きくなる】

この2つの情報から、B>Cが読み取れますね！

（Bが90°の半分よりも大きい値が確定しているので）

 

よって、\(∠C<∠B<∠A\) だとわかります。

よって、\((∠Cの向かいの辺)<(∠Bの向かいの辺)<(∠Aの向かいの辺)　⇒　AB<AC<BC\) と判断することができます。

 

 

お疲れ様でした！

これで三角形の角と辺の大小関係は理解してもらえましたか？

角と辺の大小が対応していることをおさえておけば簡単に解くことができますね＾＾

文字、式を見ているだけでは見落とし、勘違いが起こりやすいので、今回のように図を書きながら判断していくとよいですよ！

 

では、今回は以上！