【データの分析】平均値のとり得る範囲の求め方をイチから！

こんにちは！数スタの小田です。

今回は高校数学Ⅰで学習するデータの分析の単元から「平均値のとり得る範囲」についてイチから解説します。

とても簡単な問題で、3分もあれば理解できます！

この記事を通してサクッとマスターしちゃってくださいね＾＾

取り上げる問題はこちらです。

【問題】

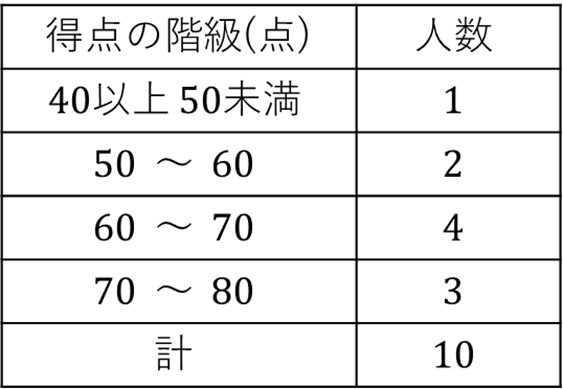
下の表は、10人のテスト結果を度数分布表にまとめたものです。このデータの平均値のとりうる値の範囲を求めなさい。

今回の内容をサクッと理解したい方は、こちらの動画がおススメです！

平均値のとりうる値の範囲を求めるやり方

平均値のとりうる値の範囲を求めるには、平均値として考えられる最小の値、最大の値をそれぞれ求める必要があります。

どういうことかというと…

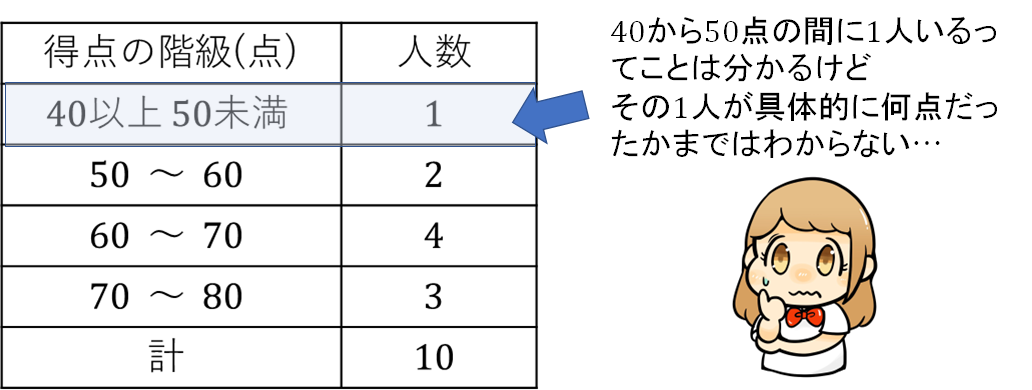
度数分布表でまとめられたデータからは、個々の値を正確に読み取ることができません。

なので、それぞれの階級に入っているデータがすべて一番小さかったパターン、大きかったパターンにおいて平均値を求めていきます。

そうすれば平均値がどれくらいの範囲をとるのかが見えてくるというわけです。

①平均値の最大を求める

それでは、まずは階級の中に入っているデータがすべて最大だった場合で考えてみましょう。

（”未満”に注意してくださいね！50未満ということは50は含まれないので最大の値は49になります）

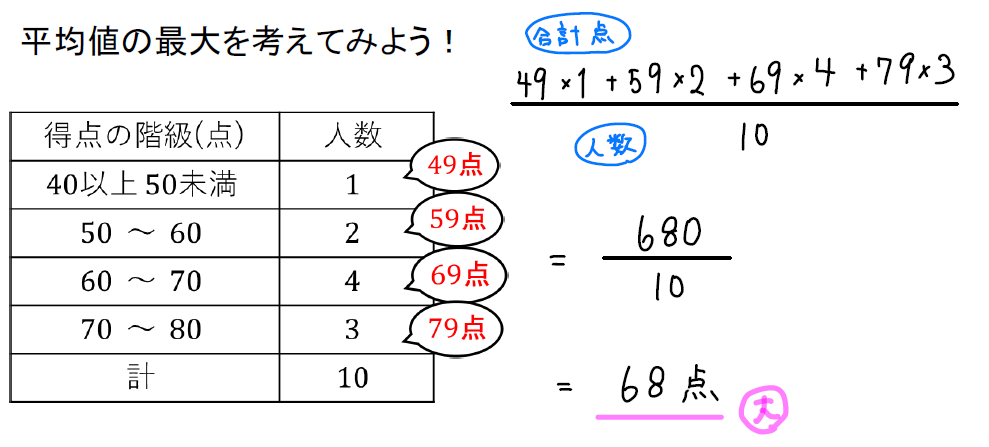
すると、こんな感じになりますね！

②平均値の最小を求める

続いて、それぞれの階級に入っているデータがすべて最小だった場合を考えます。

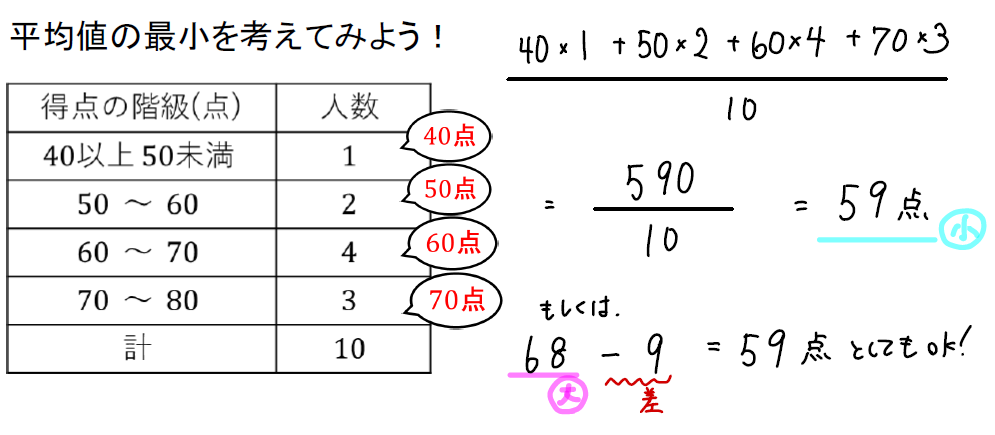
すると、こんな感じになりますね！

①で平均の最大を求めているので、そこから9を引いて求めてやってもOKです。

（階級に入っている値が最大、最小のときでは差が9になるから）

というか、こっちの方がスムーズに値を求めれますね＾＾

③平均値の範囲が求まる

①②において、平均値の最大・最小を求めることができたら

このように平均値のとりうる値の範囲が求まります。

今回の問題では平均の最大　⇒　平均の最小　という流れで求めましたが、実際に計算して体感してもらったように「平均の最小」を求める方が計算がラクです！（40、50…といったキリのよい数が出てくるから）

なので、今後問題にチャレンジするときには

平均の最小を求める　⇒　平均の最小を利用して差を用いて最大を求める

この流れだと素早く答えに辿りつくことができるのでおススメです＾＾

それでは、解き方の流れを理解してもらったところで練習問題にチャレンジしてみましょうか＾＾

練習問題

【問題】

下の表は、20人のテスト結果を度数分布表にまとめたものです。このデータの平均値のとりうる値の範囲を求めなさい。

解答・解説はこちら

答え

65点以上　74点以下

平均値の最小を求めると、

平均の最大は、最小の値に＋９すればいいので

$$65+9=\color{red}{74点}$$

まとめ

お疲れ様でした！

どうだったかな？サクッと理解できていると嬉しいです＾＾

パッと見では難しそうな問題だったかもしれませんが、平均値の最小・最大を考えればいい！ってことをしっかりと覚えておいてくださいね(‘ω’)ノ

では、今回は以上！