こんにちは!数スタの小田です。
今回は高校数学Ⅱで学習する図形と方程式の単元から「円と円の交点の座標」についてイチから解説していきます。
取り上げる問題はこちら!
【問題】次の2つの円の共有点の座標を求めなさい。
$$x^2+y^2=10, x^2+y^2-2x-y-5=0$$
今回の内容をサクッと理解したい方は、こちらの動画がおススメです!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
円と円の交点座標の求め方
【問題】次の2つの円の共有点の座標を求めなさい。
$$x^2+y^2=10, x^2+y^2-2x-y-5=0$$
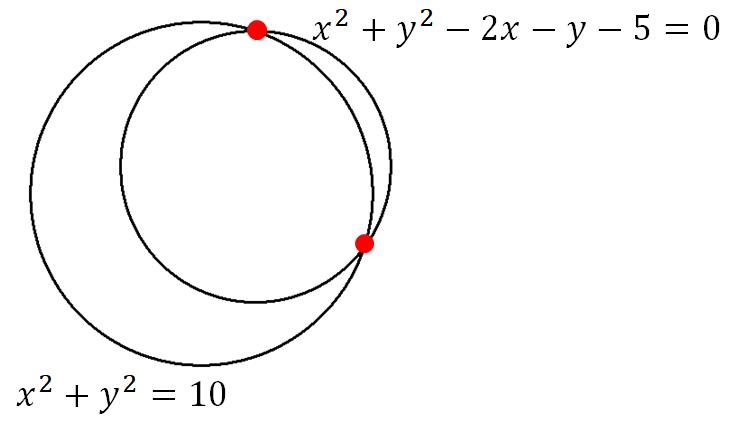
交点の座標といえば、連立方程式ですよね。
ですが、このまま2つの式を連立方程式で解こうとすると、途中で計算がつんでしまいます(^^;)
それでは、どのような手順で解いていけばいいのでしょうか。
まずは、次のように2つの式をひいて「\(x^2, y^2\)を消去」してください。
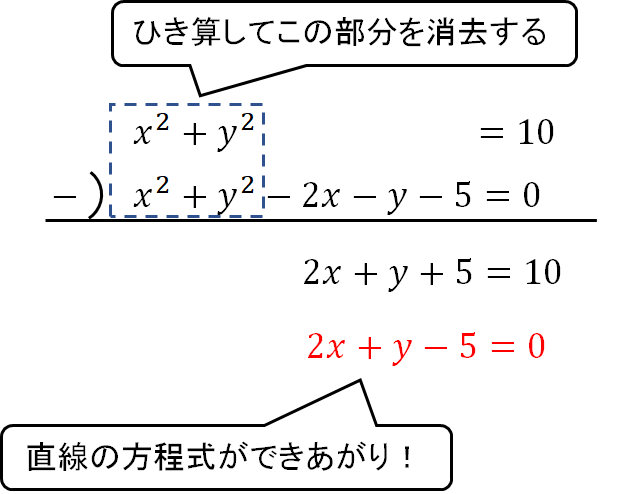
すると、直線の方程式がつくれますね。
実はこの直線の式は図の赤い部分(2つの交点を通る直線)を表した方程式となっています。
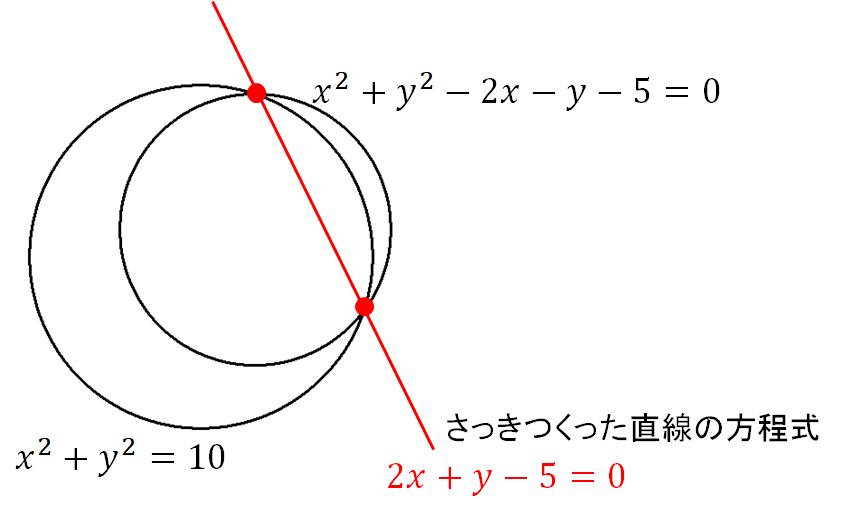
なので、この直線と円の交点を考えればOK!と捉えていけば、次のように答えを求めることができます。

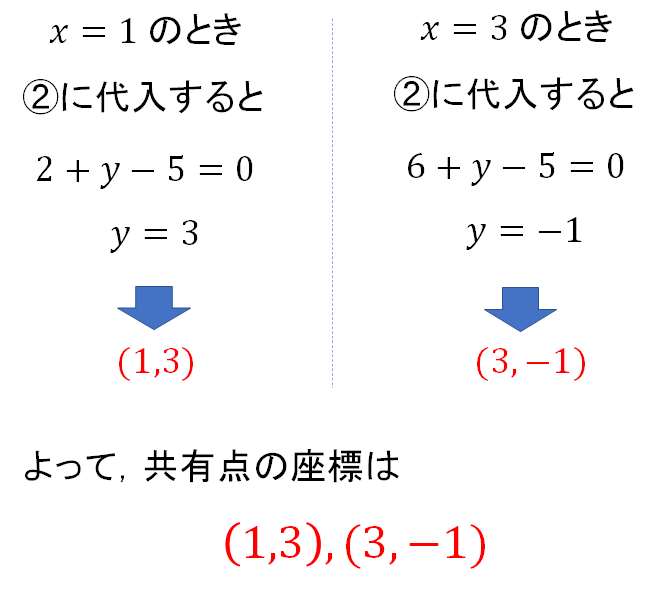
直線の式をつくってから交点を求める…
ん~、こんなの思いつかんです(^^;)
なので、円と円の交点はこのような手順でやるもんなのだ!と覚えておくといいですね^^
それでは、練習問題にチャレンジしてみましょう。
練習問題にチャレンジ!
【問題】次の2つの円の共有点の座標を求めなさい。
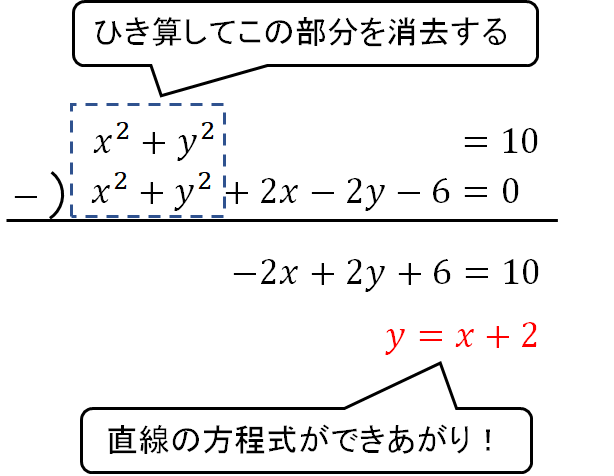
$$x^2+y^2=10, x^2+y^2+2x-2y-6=0$$
まとめ
お疲れ様でした!
最後に円と円の交点座標を求める手順をまとめておきましょう。
- 2円の方程式をひいて、直線の方程式をつくる。
- ①でつくった方程式と円の方程式を連立方程式で解く。
- 座標が求まる!
この手順はなかなか思いつかない…汗
なので、忘れてしまわぬよう定期的にこの記事を確認してやり方を思い出すようにしといてくださいね!



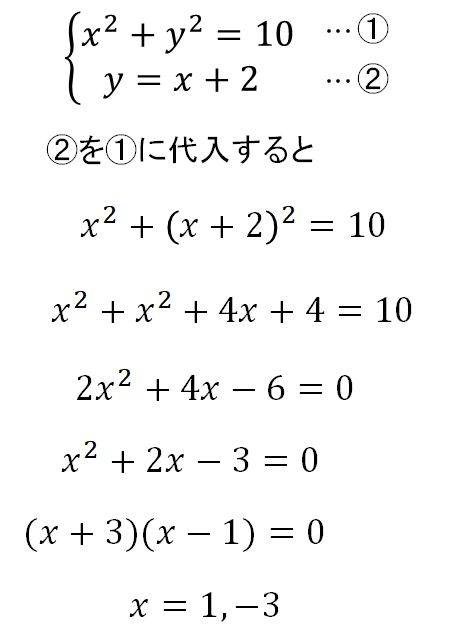















コメントを残す