今回の記事では高校数学Ⅰでデータの分析を学習している方に向けて
「箱ひげ図の見方、書き方」
についてイチから解説していきます。
箱ひげ図を理解するためには、四分位数について理解しておく必要があります。
こちらの記事もご参考ください(^^)
箱ひげ図の見方
箱ひげ図とは、データの散らばりを視覚的に分かりやすく図示したものです。
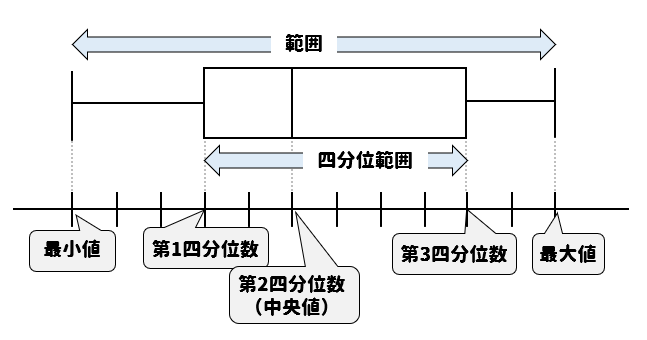
それでは、箱ひげ図の見方について解説していきます。
箱ひげ図は、箱と線（ひげ）の部分によってできています。
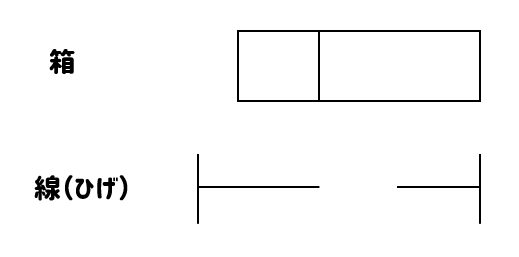
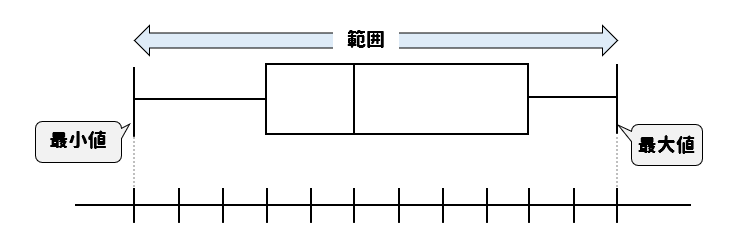
線（ひげ）の両端部分はデータの最大値と最小値を表しています。
つまり両端がどれくらい離れているかを読み取ると、それがデータの範囲ということになります。
箱の部分はそれぞれ四分位数を表しています。
第1四分位数と第3四分位数の差を四分位範囲といい、データの中心部に位置するおよそ50％のデータが含まれています。
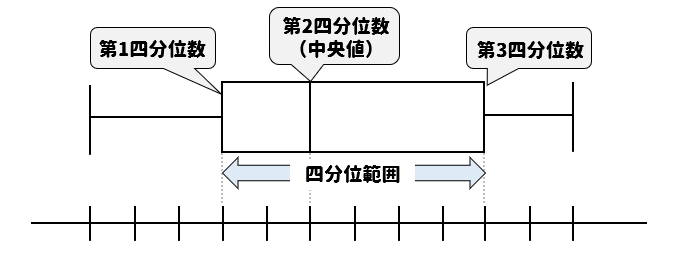
四分位数とは、データ全体を4等分するときの仕切りに位置する値のことでしたね。
つまり、このように4つ分の区画にそれぞれ25％ずつのデータが入っていることになります。
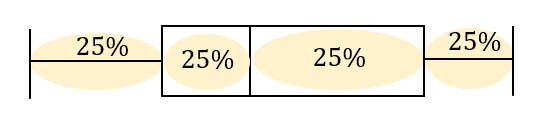
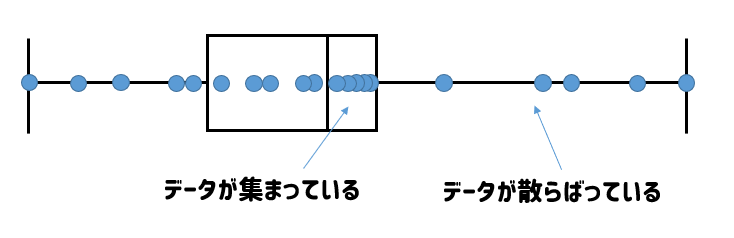
つまり、それぞれの区間には同じだけのデータが入っていることになります。
なので区間が狭くなっているところにはデータがギュッと集まっていて、区間が広いところには散らばっているのだろうということが読み取れますね。
箱ひげ図の書き方
それでは、箱ひげ図の書き方をイチから確認してみましょう。
書き方の手順は次の通りです。
- 最大値、最小値、四分位数を読み取る。
- 最大、最小から範囲を読み取り、範囲が収まるように横軸と目盛りを書く。
- 第1四分位数、第2四分位数、第3四分位数から箱の部分を書く。
- 最大値、最小値をとって、線（ひげ）の部分を書く。
- 完成！
【問題】
次のデータをもとに箱ひげ図を書きなさい。
$$2,3,3,3,4,5,7,7,8,9$$
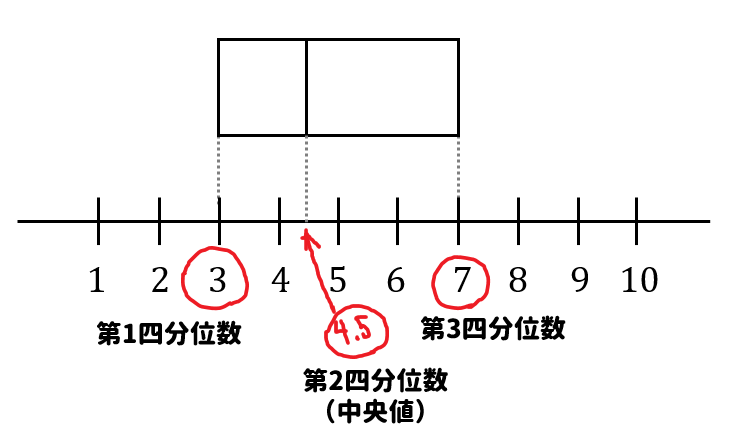
まずは最大値、最小値、四分位数をそれぞれ読み取りましょう。
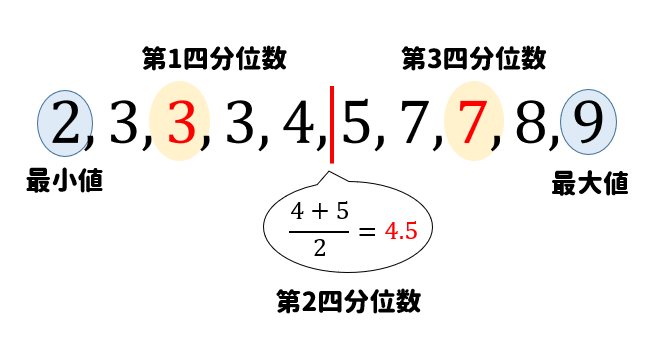
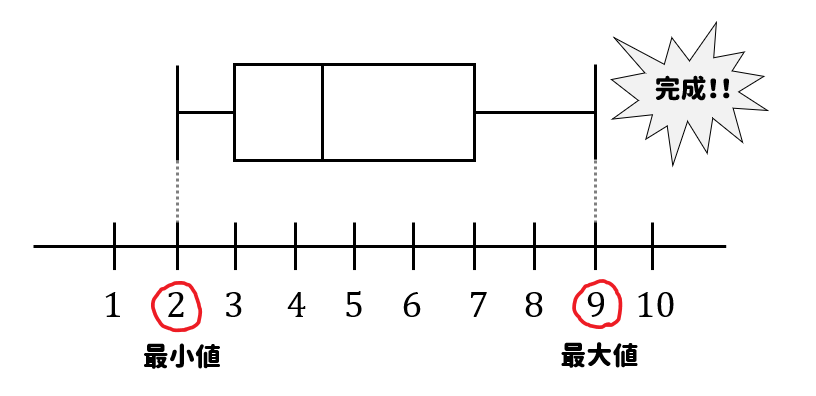
最大値9と最小値2が入るように横軸と目盛りをとります。
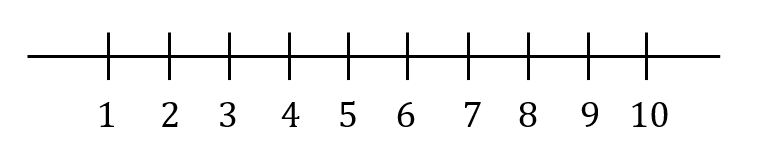
この目盛りにあわせて、第1四分位数、第2四分位数、第3四分位数から箱の部分を書きましょう。
最後に、最大値と最小値をとって箱の部分とつなげたら完成です！
まとめ！
というわけで、箱ひげ図の見方と書き方についてサクッと解説しました。
重要度としては
（見方）＞（書き方）
になるかな。
箱ひげ図を見て、データにどのような特徴があるのかを読み取れるようにしておきましょう。
LINEで質問してみる？
≫ LINE登録はこちら