こんにちは!数スタの小田です。
今回は高校数学Ⅰで学習するデータの分析の単元から「2つのデータを合わせるときの平均値、分散」について取り上げます。
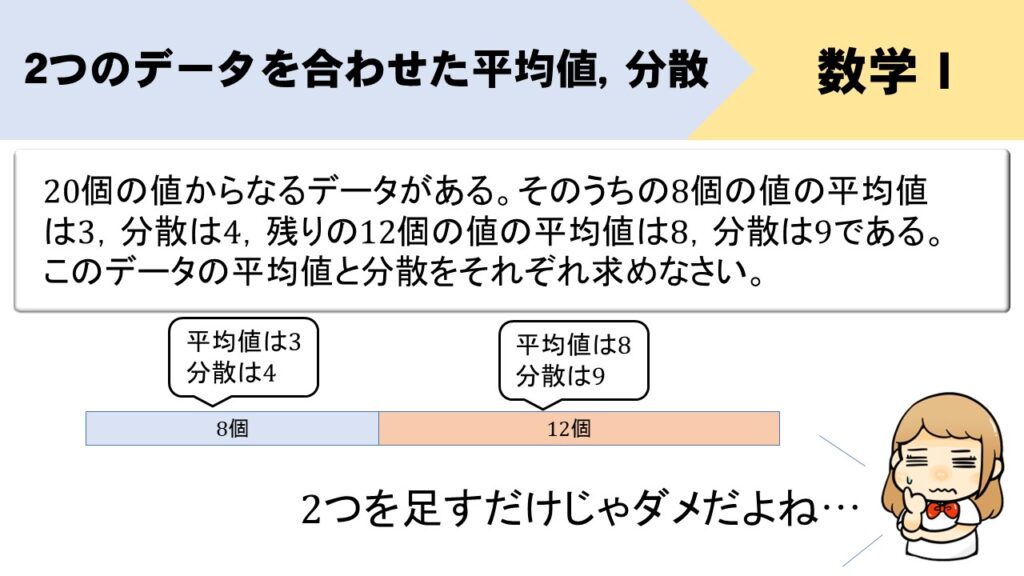
【問題】
20個の値からなるデータがある。そのうちの8個の値の平均値は3、分散は4、残りの12個の値の平均値は8、分散は9である。このデータの平均値と分散をそれぞれ求めなさい。
平均値は求めれるけど、分散がよくわからん…という方が多いと思います。今回の記事を通して、分散を求める流れとイメージをつかんでいってください^^
サクッと理解したい方は、こちらの動画も参考にしてください!
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
平均の求め方
全体の平均を求めるためには、

データの数は20と分かっているので、あとは全体(20個)のデータの合計が必要になります。
そこで、与えられている情報から
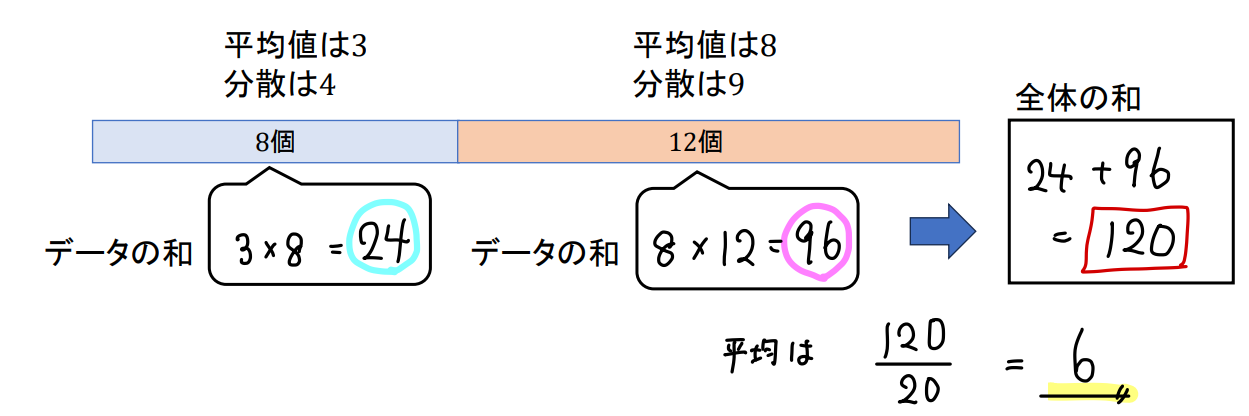
このように、それぞれ8個、12個のデータの和を求めて、全体の和を求めてしまいましょう!
和については「データの和=平均×個数」で求めることができますね。
8個のデータの平均が3なので、8個の和は\(3\times8=24\)
12個のデータの平均が8なので、12個の和は\(8\times12=96\)
全体のデータの和は、(8個の和)+(12個の和)なので、\(24+96=120\)となります。
よって、全体の平均は\(\frac{120}{20}=6\)と求まります。
答え
$$(平均) 6$$
分散の求め方
分散の求め方は2通りありましたが、ここでは2乗の平均、平均の2乗を使った方法を利用します。

全体の分散を求めるためには「全体の2乗の平均」「全体の平均の2乗」が必要です。全体の平均は先ほど求めているので、あと必要となるのは「全体の2乗の平均」ですね。
全体の2乗の平均を求めるためには、
$$2乗の平均=\frac{全体の2乗の和}{20}$$
を計算すればいいので「全体の2乗の和」を求める必要があります。
そこで次のように考えていきましょう。

分かりやすいように8個のデータを\(x_1,x_2\cdots \)、12個のデータを\(y_1,y_2\cdots\)として考えます。
\(x\)の分散が4なので、
\(xの分散=(x^2の平均)-(xの平均)^2\)
\(4=(x^2の平均)-3^2\)
\((x^2の平均)=13\)
\(\frac{x^2の和}{8}=13\)
\(x^2の和=104\)
ちょっと計算手順は長いですが(^^;)
このようにして\(x^2\)の和を求めます。
\(y\)についても同様に。
\(yの分散=(y^2の平均)-(yの平均)^2\)
\(9=(y^2の平均)-8^2\)
\((y^2の平均)=73\)
\(\frac{y^2の和}{12}=73\)
\(y^2の和=876\)
よって、全体の2乗の和は(\(x^2\)の和)+(\(y^2\)の和)なので、\(104+876=980\)となります。
このことから全体の2乗の平均が \(\frac{980}{20}=49\)と求まり、全体の分散が計算できますね!
\(全体の分散=(全体の2乗の平均)-(全体の平均)^2=49-6^2=13\)
答え
$$(分散) 13$$
分散はちょっとややこしかったですが、流れは理解してもらえましたか?
上の画像のようにイメージ図を書きながら、情報をまとめていくと計算がやりやすくなりますよ^^
やり方を理解してもらえたら、あとはご自身のワークなどを使って反復演習に取り組んでいきましょう!
では、今回は以上!
お疲れ様でした(‘ω’)ノ















コメントを残す