今回は高校数学Ⅱで学習する微分の単元から
「極限値を微分係数\(f'(a)\)を用いて表す」
について、いくつか例題を紹介しながら解説していきます。
【問題】
関数\(y=f(x)\) について、次の極限値を\(a\),\(f(a)\),\(f'(a)\)を用いて表せ。
\((1) \displaystyle \lim_{ h \to 0 } \frac{f(a-2h)-f(a)}{h} \)
\((2) \displaystyle \lim_{ h \to 0 } \frac{f(a+2h)-f(a-3h)}{h} \)
\((3) \displaystyle \lim_{ x \to a } \frac{a^2f(x)-x^2 f(a)}{x-a} \)
今回の問題のポイントは以下の通りです。

この形になるように式を上手く変形して解いていきましょう。
問題(1)の解き方
こちらの式を\(f'(a)\)を用いて表していきたいのですが、
困ったことがあります。それは…
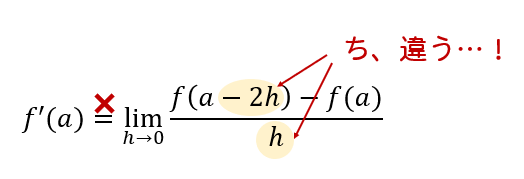
印をつけた部分が、\(-2h\)と\(h\)ということで同じ形になっていません!
なので、\(f'(a)\)に変形することができません!困った…
ですが、心配ご無用!
形が違うのなら…無理やりにでも揃えてしまえばいいのです。

ちょっと無理やりな感じはしますが、
これで形を揃えることに成功したので、\(f'(a)\)に変形することができます。

答え
$$-2f'(a)$$
問題(2)の解き方
今回の式では、\(f'(a)\)を作るための
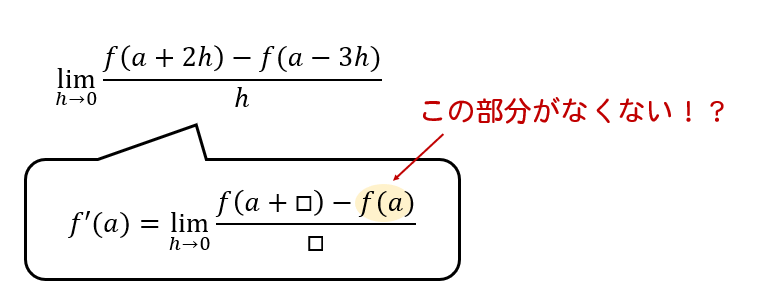
ということが分かりますね。
なので、まずは\(f(a)\)を用意してあげるところから始め、
次のように変形をしていきましょう。


答え
$$5f'(a)$$
\(f(a)\)がなければ、用意すればいい!
今回の式変形はちょっとややこしかったですが、
このように分数を2つに分けていくやり方もある。
ということを頭に入れておいてください。
問題(3)の解き方
今回の問題では、

こちらの形で変形をしていきましょう!
まぁ、どちらの形を利用すればよいかは、式を見るとだいたい予測がつきますね。
\(lim\)の部分、分母が\(h\)、\(x,a\)のどちらなのかなど。
今回の問題では、ちょっと邪魔なものが含まれています。

これらのジャマものをなくすためには、
共通因数としてくくり出してやればいいじゃないか!
という発想になります。
というわけで、
共通因数でくくり出せるようにパーツを準備。
そして、分数を2つに分けながら式を整理していきましょう。
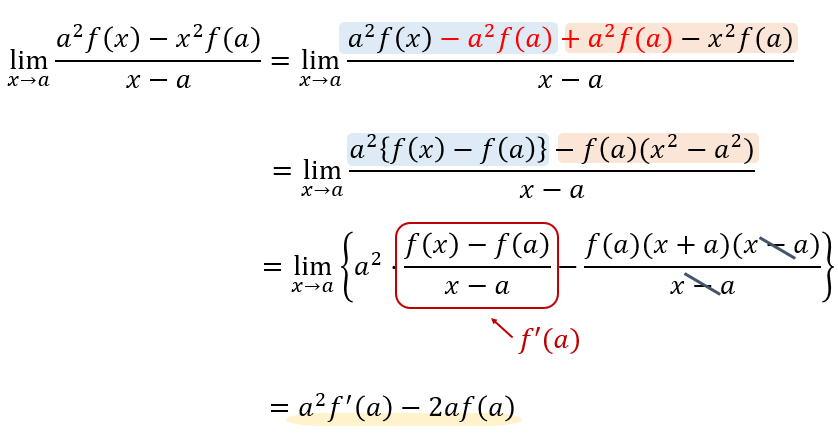
答え
$$a^2f'(a)-2af(a)$$
まとめ!
お疲れ様でした!
今回の問題を解くためには、
まず微分係数の定義をしっかりと覚えておきましょう。

今回の問題では、分数や\(f(x)\)など
見た目がゴチャッとするモノが多いため、途中式が複雑になりがちです。
やり方は分かっていたけど、答えが出なかった…
というのはもったいないですから、
問題を解くときには余白を取りながら丁寧に式を書いていくようにしましょうね!















(1)の問題文が違うような気がします。
ご指摘ありがとうございます!
訂正しておきましたm(__)m
(3)で、答えにf’(a)だけでなくf(a)が含まれていても良いのですか?
問題にそう書いてあるので大丈夫です!
うれしいい