【数学Ⅱ】微分で体積、表面積の変化率を求める問題を解説！

今回は数学Ⅱで学習する微分積分の単元から

「体積・表面積の変化率を求める」

について解説していきます。

この問題は微分を用いると、簡単に答えを求めることができます。

ですが、なんで微分をする必要があるの？

という疑問を抱きやすい問題でもあります。

変化率を求めるために、なぜ微分をする必要があるのか。

イチから確認していきましょう(/・ω・)/

平均変化率と瞬間の変化率

今回の問題を解くためには、

まず、問題文で何を問われているのかをハッキリとさせておく必要があります。

5秒後の変化率とはどういう意味なのか確認しておきましょう。

3秒から5秒後までの変化率を求めなさい。

このように、3～5秒といったある一定の区間において、

どれくらいのペースで変化しているかを表した値を平均変化率といいます。

中学の理科で学習した平均の速さと同じ考え方ですね！

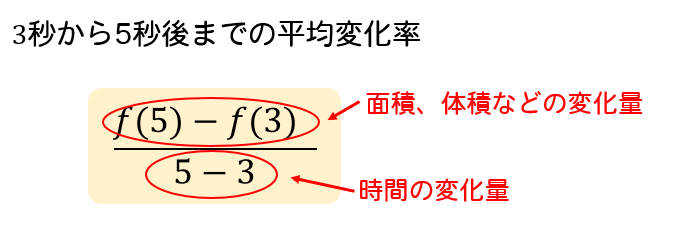
このように、どれくらいの時間で

どれくらいの面積、体積が変化したのかを計算すればよいです。

それに対して、今回の問題で問われているように

5秒後という一瞬の間にどれくらい変化しているかを表した値を瞬間の変化率といいます。

問題文では、瞬間という言葉は使われず変化率とだけ書かれています。

こちらは中学の理科で学習した瞬間の速さと同じ考え方ですね！

瞬間の変化率というのは、0.0000001秒のように

ほんとに一瞬の間のこととして考えていきます。

なので、イメージとしてはこんな式になります。

ただ、こんなのはとても計算してられませんよね(^^;)

そこで利用していくのが極限(lim)です。

上の式を次のように変換して考えていくと、

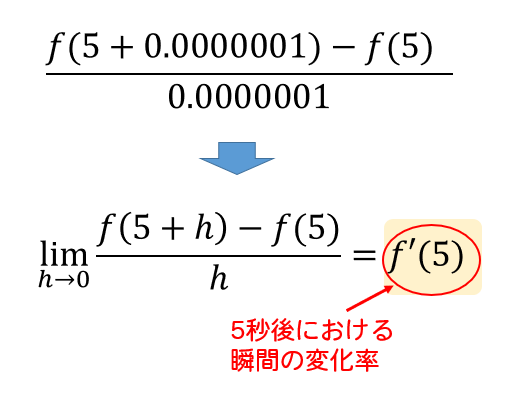
瞬間の変化率というのは、微分係数を求めることと同じなんだな！

ってことが理解できますよね。

というわけで、

前置きがかなり長くなってしまいましたが、

今回の問題のように瞬間の変化率を求めたい場合には、

微分を利用して求める！ということになります。

解き方を確認！

まずは、SとVの式を作りましょう。

そして、それらを微分することで5秒後の変化率を求めていきます。

毎秒1㎝ずつ半径が大きくなっていくので、

\(t\)秒後の半径の大きさは、\(t\)㎝分だけ大きくなっているはずなので、

\((1+t)\)㎝と表すことができます。

すると、球の公式を利用して

S、Vは次のように表すことができます。

\(S=4\pi(t+1)^2=4\pi(t^2+2t+1)\)

\(V=\frac{4}{3}\pi(t+1)^3=\frac{4}{3}\pi(t^3+3t^2+3t+1)\)

そして、それぞれを\(t\)で微分していくと

\(S’=8\pi(t+1)\)

\(V’=4\pi(t^2+2t+1)\)

となります。

求めたいのは5秒後における変化率（微分係数）ですので、

\(S’,V’\)にそれぞれ\(t=5\)を代入していけば完成となります。

\(t=5\)のとき、

\(S’=8\pi (5+1)=48\pi\)

\(V’=4\pi(5^2+2\dot 5+1)=144\pi\)  となりました。

よって、答えは

\(cm^2/s\)、\(cm^3/s\)ってなに！？

見たことないけど…！！

となってしまった人がいるかもしれませんね。

ですが、意味は簡単なことですよ(^^)

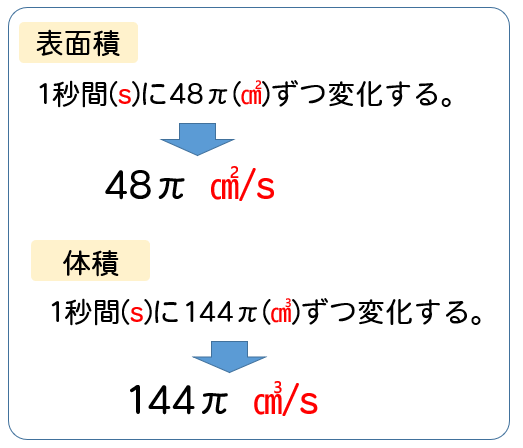
表面積の単位が㎠、体積の単位が㎤だから

変化率の単位もそれに合わせてるってことですね。

練習問題に挑戦！

まとめ！

お疲れ様でした！

瞬間の変化率、速度を求めたい場合には、

微分係数を求めればよい！

ということを覚えておけば簡単な問題ですね(^^)

ただ、

高校生になると球の公式を使う場面が減ってしまうため、

公式忘れで解けませんでした…

なんていう悲劇も起こりえます(^^;)

そうならないためにも球の公式は必ず覚えておいてくださいね。

語呂合わせで覚えるのがおススメですよ！

>【球の体積・表面積】公式の覚え方は語呂合わせで！問題を使って解説！