今回の記事では、高校数学Ⅰで学習する集合と命題の単元から
「対偶を利用した証明の解答例」
についてまとめておきます。
対偶を利用した証明って、
あれ、どんな手順で解くんだっけ?(^^;)
と忘れてしまいがちです。
そんなときのために、この記事ではいろんなパターンの解答例をまとめておきます。
対偶の証明を利用する場面
次の場面において、対偶を利用すると証明がラクになります。
結論が簡単なとき!

このように、仮定よりも結論の方が簡単な場合には対偶を利用することで簡単に証明ができるようになります。
結論が「~または~」のとき!
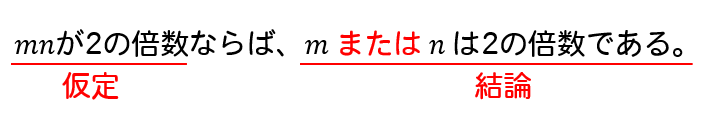
結論が「または」の形になっている場合、対偶をとると仮定を「かつ」に変換することができます。すると、証明がラクになってきます。
対偶の証明(奇数)
【問題】
\(n\)は整数とする。対偶を利用して、次の命題を証明せよ。
\(n^2\) が奇数ならば、\(n\)は奇数である。
【解答】
もとの命題の対偶をとると「\(n\)が偶数ならば、\(n^2\)は偶数である」となり、これを証明する。
\(n\)は偶数だから、\(k\)(整数)を用いて、\(n=2k\) と表される。
このとき、\(n^2=(2k)^2=4k^2=2\cdot2k^2\) となる。
\(2k^2\) は整数だから、\(n^2\) は偶数である。
よって、対偶が証明されたから、もとの命題も成り立つ。
ポイント!
- 偶数(2の倍数) ⇒ \(2\times (整数)\)
- 奇数 ⇒ \(2\times (整数) +1\)
対偶の証明(偶数、2の倍数)
【問題】
\(n\)は整数とする。次の命題を証明せよ。
\(n^2\) が2の倍数ならば、\(n\)は2の倍数である。
【解答】
もとの命題の対偶をとると「\(n\)が2の倍数でないならば、\(n^2\)は2の倍数でない」となり、これを証明する。
\(n\)は2の倍数でないから、\(k\)(整数)を用いて、\(n=2k+1\) と表される。
このとき、
\(n^2=(2k+1)^2=4k^2+4k+1=2(2k^2+2k)+1\) となる。
\(2k^2+2k\) は整数だから、\(n^2\) は2の倍数でない。
よって、対偶が証明されたから、もとの命題も成り立つ。
ポイント!
- 2の倍数=偶数
- 2の倍数でない=奇数
対偶の証明(3の倍数)
【問題】
\(n\)は整数とする。次の命題を証明せよ。
\(n^2\) が3の倍数ならば、\(n\)は3の倍数である。
【解答】
もとの命題の対偶をとると「\(n\)が3の倍数でないならば、\(n^2\)は3の倍数でない」となり、これを証明する。
\(n\)は3の倍数でないから、\(k\)(整数)を用いて、\(n=3k+1\) または \(n=3k+2\) と表される。
\(n=3k+1\) のとき
$$\begin{eqnarray}n^2&=&(3k+1)^2\\[5pt]&=&9k^2+6k+1\\[5pt]&=&3(3k^2+2k)+1 \end{eqnarray}$$
\(n=3k+2\) のとき
$$\begin{eqnarray}n^2&=&(3k+2)^2\\[5pt]&=&9k^2+12k+4\\[5pt]&=&3(3k^2+4k+1)+1 \end{eqnarray}$$
\(3k^2+2k\)、\(3k^2+4k+1\) は整数だから、\(n^2\) は3の倍数でない。
よって、対偶が証明されたから、もとの命題も成り立つ。
ポイント!
- 3の倍数 ⇒ \(3k\) (\(k\):整数)
- 3の倍数でない ⇒ \(3k+1\) , \(3k+2\) (\(k\):整数)
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
対偶の証明(または2の倍数)
【問題】
\(m,n\)は整数とする。次の命題を証明せよ。
\(mn\) が2の倍数ならば、\(m\) または \(n\) は2の倍数である。
【解答】
もとの命題の対偶をとると「\(m,n\)がともに2の倍数でないならば、\(mn\)は2の倍数でない」となり、これを証明する。
\(m,n\)は2の倍数でないから、\(k,l\)(整数)を用いて、\(m=2k+1\) , \(n=2l+1\) と表される。
このとき、
$$\begin{eqnarray}mn&=&(2k+1)(2l+1)\\[5pt]&=&4kl+2k+2l+1\\[5pt]&=&2(2kl+k+l)+1 \end{eqnarray}$$
\(2kl+k+l\) は整数であるから、\(mn\) は2の倍数でない。
よって、対偶が証明されたから、もとの命題も成り立つ。
ポイント!
- 「または」の否定は「かつ」になる。
- \(k,l\)の2種類の文字を使って表す。
対偶の証明(または3の倍数)
【問題】
\(m,n\)は整数とする。次の命題を証明せよ。
\(mn\) が3の倍数ならば、\(m\) または \(n\) は3の倍数である。
【解答】
もとの命題の対偶をとると「\(m,n\)がともに3の倍数でないならば、\(mn\)は3の倍数でない」となり、これを証明する。
\(m,n\)は3の倍数でないから、\(k,l\)(整数)を用いて、
\(m=3k+1\) または \(m=3k+2\)
\(n=3l+1\) または \(n=3l+2\) と表せる。
〔1〕\(m=3k+1\), \(n=3l+1\) のとき
$$\begin{eqnarray}mn&=&(3k+1)(3l+1)\\[5pt]&=&9kl+3k+3l+1\\[5pt]&=&3(3kl+k+l)+1 \end{eqnarray}$$
\(3kl+k+l\) は整数だから、\(mn\)は3の倍数でない。
〔2〕\(m=3k+1\), \(n=3l+2\) のとき
$$\begin{eqnarray}mn&=&(3k+1)(3l+2)\\[5pt]&=&9kl+6k+3l+2\\[5pt]&=&3(3kl+2k+l)+2 \end{eqnarray}$$
\(3kl+2k+l\) は整数だから、\(mn\)は3の倍数でない。
〔3〕\(m=3k+2\), \(n=3l+1\) のとき
$$\begin{eqnarray}mn&=&(3k+2)(3l+1)\\[5pt]&=&9kl+3k+6l+2\\[5pt]&=&3(3kl+k+2l)+2 \end{eqnarray}$$
\(3kl+k+2l\) は整数だから、\(mn\)は3の倍数でない。
〔4〕\(m=3k+2\), \(n=3l+2\) のとき
$$\begin{eqnarray}mn&=&(3k+2)(3l+2)\\[5pt]&=&9kl+6k+6l+4\\[5pt]&=&3(3kl+2k+2l+1)+1 \end{eqnarray}$$
\(3kl+2k+2l+1\) は整数だから、\(mn\)は3の倍数でない。
〔1〕~〔4〕より、対偶が証明されたから、もとの命題も成り立つ。
ポイント!
- 4パターンの場合分けが必要。
対偶の証明(積)
【問題】
\(m,n\)は整数とする。次の命題を証明せよ。
\(m^2+n^2\) が奇数ならば、\(mn\) は偶数である。
【解答】
もとの命題の対偶をとると「\(mn\)が奇数ならば、\(m^2+n^2\)は偶数である」となり、これを証明する。
\(mn\)が奇数ならば、\(m,n\) はともに奇数になる。
よって、\(k,l\)(整数)を用いて、\(m=2k+1\) , \(n=2l+1\) と表される。
このとき、
$$\begin{eqnarray}m^2+n^2&=&(2k+1)^2+(2l+1)^2\\[5pt]&=&4k^2+4k+1+4l^2+4l+1\\[5pt]&=&2(2k^2+2l^2+2k+2l+1) \end{eqnarray}$$
\(2k^2+2l^2+2k+2l+1\) は整数であるから、\(m^2+n^2\) は偶数である。
よって、対偶が証明されたから、もとの命題も成り立つ。
ポイント!
- \(mn\)が奇数 ⇒ \(m,n\) がともに奇数
- \(mn\)が偶数 ⇒ \(m,n\) のどちらか一方が偶数
対偶の証明(無理数)
【問題】
\(x,y\)は実数とする。次の命題を証明せよ。
\(x+y\) が無理数ならば、\(x,y\) の少なくとも一方は無理数である。
【解答】
もとの命題の対偶をとると「\(x,y\)がともに有理数ならば、\(x+y\)は有理数である」となり、これを証明する。
\(x,y\)がともに有理数ならば、整数 \(a,b,c,d\) ( ただし、\(b≠0, d≠0\) ) を用いて
\(x=\frac{a}{b}\), \(y=\frac{c}{d}\) と表せる。
このとき、
$$\begin{eqnarray}x+y&=&\frac{a}{b}+\frac{c}{d}\\[5pt]&=&\frac{ad+bc}{bd} \end{eqnarray}$$
\(bd\),\(ad+bc\) はともに整数であるから、\(x+y\) は有理数である。
よって、対偶が証明されたから、もとの命題も成り立つ。
ポイント!
- 有理数は、分数で表せる数のこと。
まとめ!
お疲れ様でした!
対偶を利用した証明をマスターするには、
パターンを身につけておくのがよいです。
今回紹介した問題を何度も練習して、考え方を身につけておいてくださいね!
対偶の証明をマスターしたら、次は背理法の証明にも挑戦していきましょう!















分からないことだらけでしたが、とても分かりやすく、実践も出来たので、証明の力がつきました!ありがとうございます。