今回の記事では「等差数列」についてイチから解説してきます。
等差数列というのは…
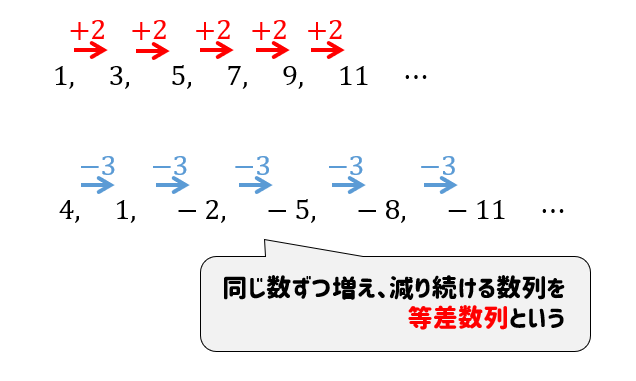
このように、同じ数だけ増えたり減ったリする数列のことだね。
この数列の第\(n\)番目の数は?
数列の和はどうなる?
といった基本的な問題の解き方などを学んでいこう!
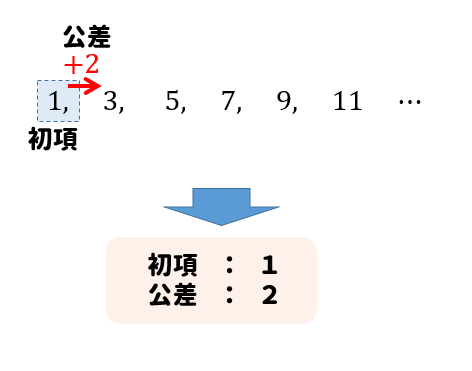
ちなみに、一番最初の項を初項、等差数列の変化していく値のことを公差というので、それぞれ覚えておいてね。
それぞれの項目のところに解説動画も用意しているので参考にしてくださいね^^
等差数列の考え方!【一般項の公式】
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
等差数列の一般項を求める公式
$$a_n=a+(n-1)d$$
$$a:初項 d:公差$$
この公式を覚えてしまえば、等差数列の第\(n\)番目の項が何になる?という問題は楽勝です。
だけど、文字が多くてなんかイヤだ!
っていう人もいるはず(^^;)
なので、なぜこのような公式によって等差数列の一般項を求めることができるのか?について簡単に説明しておきますね。
等差数列の項を求める場合
その項は、初項からどれだけ公差が加えられて出来上がったものなのか?
を考えてみましょう!
例えば、次の等差数列を考えてみると
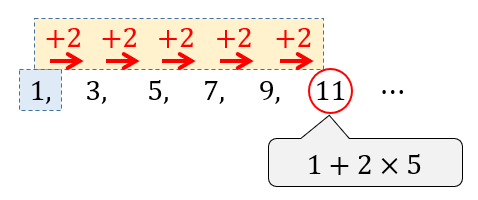
第6項の数は、初項から公差を5回加えて出来上がっているってことが分かるよね!
第10項であれば、初項から公差を9回。
第100項であれば、初項から公差を99回。
というように、求めたい項からマイナス1した回数だけ公差が加えられていることに気が付くはずです。
そうなれば、第\(n\)項の場合には?
文字がでてきても考えは同じだね!マイナス1をした\((n-1)\)回だけ公差が加えられているってことだ。
つまり!
等差数列の第\(n\)項は、初項に公差を\((n-1)\)回だけ加えた数ってことなので
$$\begin{eqnarray}a_n=a+(n-1)d \end{eqnarray}$$
こういった公式ができあがるわけですね!
等差数列の一般項に関する問題解説!
では、一般項の公式を使って問題を解いてみましょう。
初項が\(4\)、公差が\(3\)である等差数列\(\{a_n\}\)の一般項を求めなさい。
また、第\(9\)項を求めなさい。
第\(3\)項が\(15\)、第\(5\)項が\(21\)である等差数列\(\{a_n\}\)の一般項を求めなさい。
また、\(186\)は第何項になるか求めなさい。
3つの等差数列【等差中項】
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
等差中項
3つの項の等差数列\(a, b, c\)について、次の式が成り立つ。
$$2b=a+c$$
こうやって公式だけ見てしまうと難しく感じてしまいますが、単純なことです。
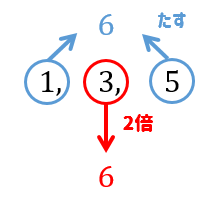
真ん中の数を2倍すると、両端の数を足したものに等しくなるってことですね!
このとき、真ん中にある項のことを両端の項の等差中項といいます。
よくでてくる用語なので覚えておきましょう!
なぜ、等差数列はこのような関係になっているのか。
これは簡単に証明ができます。
\(a\)と\(b\)、\(b\)と\(c\)の差を考えてみましょう。

等差数列とは、その名の通り
差が等しいわけですから
$$b-a=c-b$$
という関係式ができます。
これを変形すると
$$\begin{eqnarray}b-a&=&c-b\\[5pt]2b&=&a+c \end{eqnarray}$$
となるわけですね!
簡単、簡単(^^)
等差中項に関する問題解説!
では、等差中項を使って問題を解いてみましょう。
数列 \(4, x, -6\) が等差数列であるとき、\(x\)の値を求めなさい。
等差数列をなす3数があって、その和は\(27\)で、積は\(45\)である。この3数を求めなさい。
等差数列の和【和の公式】
動画の資料はメルマガ講座の中でお渡ししています。無料で登録できるのでこちらからお願いします^^
等差数列の和を求める公式
$$S_n=\frac{1}{2}n(a+l)$$
$$S_n=\frac{1}{2}n\{2a+(n-1)d\}$$
$$a:初項 l:末項 n;項数$$
等差数列の和を求めるときに使うのが上の公式です。
2パターンの公式があるのですが、別物だとは思わないでくださいね。
末項(\(a_n\))を一般項の公式を用いて、\(a_n=a+(n-1)d\) として考えたのが下の式です。
$$\begin{eqnarray}S_n&=&\frac{1}{2}n(a+l)\\[5pt]&=&\frac{1}{2}n\{a+a+(n-1)d\}\\[5pt]&=&\frac{1}{2}n\{2a+(n-1)d\} \end{eqnarray}$$
こうやって導くことができるね!
等差数列の和の公式が覚えれないよ…って方は
\(S_n=\frac{1}{2}n(a+l)\) だけ覚えておけば大丈夫ですね!
なんで、こんな公式で等差数列の和が求まるの??
という疑問を抱いてしまった方に向けて「公式のなぜ?」についても解説しておきます。
文字を使って考えてしまうと複雑に見えちゃうので、具体例を使って考えてみよう。
次の等差数列の和を求めなさい。
$$1,3,5,7,9,11$$
和を求めたい等差数列の項を大小が逆になるように並べ替えたものを用意します。
そして、元の数列と並べ替えた数列をそれぞれ足すと…
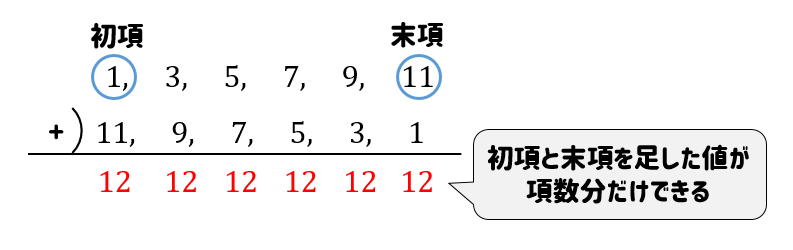
このようにすべて同じ値(初項と末項を足したもの)になっていることが分かるね。
これらを全部足すと、求めたい等差数列の和の2倍になるはずだ。
なので、求めたい等差数列の和は次のような式で求めることができます。

初項と末項を足したものが項数分だけできる。
そして、それを半分にすれば求めたい等差数列の和になっている。
ってことだね。
$$S=(1+11)\times 6\times \frac{1}{2}=33$$
これを文字でかっこよく書いたものが等差数列の和の公式ってことです。
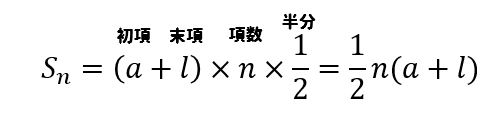
等差数列の和に関する問題解説!
では、等差数列の和の公式を使って問題を解いてみましょう。
初項が\(3\)、末項が\(27\)、項数が\(6\)である等差数列の和を求めなさい。
初項が\(60\)、公差が\(-6\)の等差数列の初項から第\(10\)項までの和を求めなさい。
次の等差数列の和を求めなさい。
$$2,6,10,14,\cdots ,90$$
初項が\(61\)、公差が\(-4\)である等差数列の初項からの和が最大となるのは第何項のときか。また、そのときの和を求めなさい。
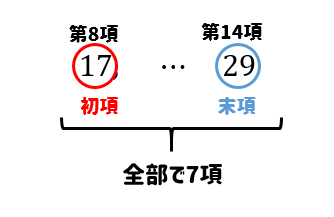
初項が\(3\)、公差が\(2\)である等差数列の第\(8\)項から第\(14\)項までの和を求めなさい。
等差数列の公式【まとめ!】
では、最後に等差数列の公式をまとめておきましょう!
等差数列の一般項を求める式$$a_n=a+(n-1)d$$
$$a:初項 d:公差$$
等差中項
3つの項の等差数列\(a, b, c\)について、次の式が成り立つ。
$$2b=a+c$$
等差数列の和を求める公式
$$S_n=\frac{1}{2}n(a+l)$$
$$S_n=\frac{1}{2}n\{2a+(n-1)d\}$$
$$a:初項 l:末項 n;項数$$













コメントを残す